Tuần 22: Diện tích xung quanh và diện tích toàn phần của hình lập phương. Thể tích của một hình - trang 17
Giải Cùng em học Toán lớp 5 tập 2 tuần 22 Diện tích xung quanh và diện tích toàn phần của hình lập phương. Thể tích của một hình trang 17 với lời giải chi tiết. Câu 1. Người ta muốn sơn mặt ngoài (kể cả đáy) của hai chiếc hộp nhựa (dạng hình hộp chữ nhật) để trồng hoa có kích thước như hình dưới đây. Tính diện tích cần sơn.
Bài 1
Người ta muốn sơn mặt ngoài (kể cả đáy) của hai chiếc hộp nhựa (dạng hình hộp chữ nhật) để trồng hoa có kích thước như hình dưới đây. Tính diện tích cần sơn.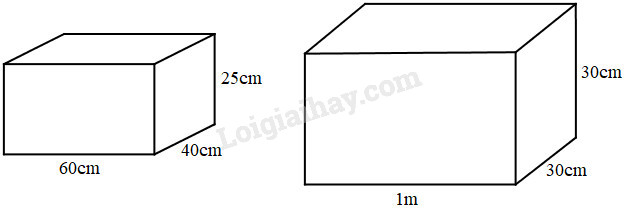
Phương pháp giải:
Vì hai chiếc hộp nhựa dùng để trồng hoa nên hai chiếc hộp đó không có nắp, vì thế mỗi chiếc hộp nhựa cần sơn \(1\) mặt đáy và \(4\) mặt bên.
+ Diện tích xung quanh của mỗi chiếc hộp nhựa = chu vi đáy x chiều cao.
+ Diện tích đáy của hộp = chiều dài x chiều rộng.
+ Diện tích cần sơn của mỗi hộp = diện tích xung quanh của hộp + diện tích đáy.
- Tính diện tích cần sơn của cả hai hộp nhựa.
Lời giải chi tiết:
+) Với chiếc hộp nhựa bên trái:
Diện tích xung quanh của hộp nhựa đó là:
\((60 + 40) \times 2 \times 25 = 5000\,\,(c{m^2})\)
Diện tích đáy của hộp nhựa đó là:
\(60 \times 40 = 2400\,\,(c{m^2})\)
Diện tích cần sơn của hộp nhựa là:
\(5000 + 2400 = 7400\,\,(c{m^2})\)
+) Với chiếc hộp nhựa bên phải:
Đổi \(1m = 100cm\)
Diện tích xung quanh của hộp nhựa đó là:
\((100 + 30) \times 2 \times 30 = 7800\,(c{m^2})\)
Diện tích đáy của hộp nhựa đó là:
\(100 \times 30 = 3000\,\,(c{m^2})\)
Diện tích cần sơn của hộp nhựa là:
\(7800 + 3000 = 10800\,\,(c{m^2})\)
Diện tích cần sơn của cả hai chiếc hộp đó là:
\(7400 + 10800 = 18200\,\,(c{m^2})\)
Đáp số: \(18200c{m^2}\).
Bài 2
Viết số đo thích hợp vào ô trống:
|
Hình lập phương |
A |
B |
C |
|
Độ dài cạnh |
12cm |
8,5dm |
\(\dfrac{3}{4}\)m |
|
Diện tích xung quanh |
|
|
|
|
Diện tích toàn phần |
|
|
|
Phương pháp giải:
- Muốn tính diện tích xung quanh của hình lập phương ta lấy diện tích một mặt nhân với \(4\).
- Muốn tính diện tích toàn phần của hình lập phương ta lấy diện tích một mặt nhân với \(6\).
Lời giải chi tiết:
a) Hình lập phương A:
Diện tích một mặt của hình lập phương đó là:
\(12 \times 12 = 144\,\,(c{m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(144 \times 4 = 576\,\,(c{m^2})\)
Diện tích toàn phần của hình lập phương đó là:
\(144 \times 6 = 864\,\,(c{m^2})\)
b) Hình lập phương B:
Diện tích một mặt của hình lập phương đó là:
\(8,5 \times 8,5 = 72,25\,\,(d{m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(72,25 \times 4 = 289\,\,(d{m^2})\)
Diện tích toàn phần của hình lập phương đó là:
\(72,25 \times 6 = 433,5\,\,(d{m^2})\)
c) Hình lập phương C:
Diện tích một mặt của hình lập phương đó là:
\(\dfrac{3}{4} \times \dfrac{3}{4} = \dfrac{9}{{16}}\,\,({m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(\dfrac{9}{{16}} \times 4 = \dfrac{9}{4}\,\,({m^2})\)
Diện tích toàn phần của hình lập phương đó là:
\(\dfrac{9}{{16}} \times 6 = \dfrac{{27}}{8}\,\,({m^2})\)
Ta có kết quả như sau :
|
Hình lập phương |
A |
B |
C |
|
Độ dài cạnh |
12cm |
8,5dm |
\(\dfrac{3}{4}\)m |
|
Diện tích xung quanh |
576cm2 |
289dm2 |
\(\dfrac{9}{4}\)m2 |
|
Diện tích toàn phần |
864cm2 |
433,5dm2 |
\(\dfrac{27}{8}\)m2 |
Bài 3
Đúng ghi Đ, sai ghi S:
Cho hình A và hình B như dưới đây:
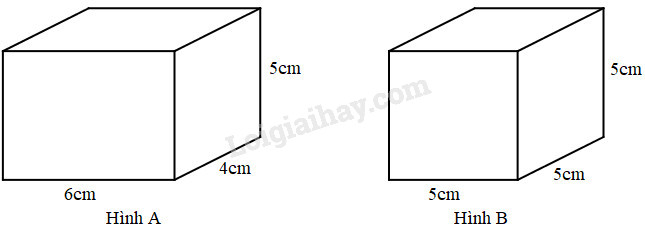
|
a) Hình A có diện tích toàn phần bé hơn hình B |
|
|
b) Hình B có diện tích xung quanh bé hơn hình A |
|
|
c) Hình A và hình B có diện tích xung quanh bằng nhau |
|
Phương pháp giải:
- Hình A là hình hộp chữ nhật có chiều dài \(6cm\), chiều rộng \(4cm\) và chiều cao là \(5cm\)
- Diện tích xung quanh của hình hộp chữ nhật = chu vi đáy nhân với chiều cao.
- Diện tích toàn phần của hình hộp chữ nhật = diện tích xung quanh + diện tích hai mặt đáy.
- Hình B là hình lập phương có cạnh là \(5cm\).
- Diện tích xung quanh của hình lập phương = diện tích một mặt nhân với \(4\).
- Diện tích toàn phần của hình lập phương = diện tích một mặt nhân với \(6\).
Lời giải chi tiết:
+) Hình hộp chữ nhật A:
Chu vi đáy của hình hộp chữ nhật là:
\((6 + 4) \times 2 = 20\,\,(cm)\)
Diện tích xung quanh của hình hộp chữ nhật là:
\(20 \times 5 = 100\,\,(c{m^2})\)
Diện tích đáy của hình hộp chữ nhật là:
\(6 \times 4 = 24\,\,(c{m^2})\)
Diện tích toàn phần của hình hộp chữ nhật là:
\(100 + 24 \times 2 = 148\,\,(c{m^2})\)
+) Hình lập phương B:
Diện tích một mặt của hình lập phương đó là:
\(5 \times 5 = 25\,\,(c{m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(25 \times 4 = 100\,\,(c{m^2})\)
Diện tích toàn phần của hình lập phương đó là:
\(25 \times 6 = 150\,\,(c{m^2})\)
Ta có:
\(100c{m^2} = 100c{m^2}\,;\, 148c{m^2} < 150c{m^2}\)
Do đó, hình A và hình B có diện tích xung quanh bằng nhau; hình A có diện tích toàn phần bé hơn hình B.
Vậy ta có bảng kết quả như sau :
|
a) Hình A có diện tích toàn phần bé hơn hình B |
Đ |
|
b) Hình B có diện tích xung quanh bé hơn hình A |
S |
|
c) Hình A và hình B có diện tích xung quanh bằng nhau |
Đ |
Bài 4
Tính diện tích xung quanh, diện tích toàn phần của các hình dưới đây:
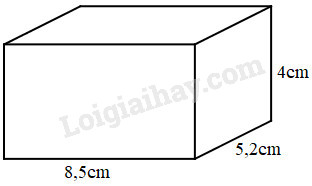
a)
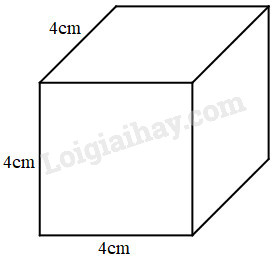
b)
Phương pháp giải:
a) Hình ở câu a là hình hộp chữ nhật có chiều dài \(8,5cm\), chiều rộng \(5,2cm\) và chiều cao là \(4cm\).
- Diện tích xung quanh = chu vi đáy x chiều cao.
- Diện tích toàn phần= diện tích xung quanh + diện tích 2 mặt hai đáy.
b) Hình B là hình lập phương có cạnh là \(4cm\).
- Diện tích xung quanh của hình lập phương = diện tích một mặt nhân với \(4\).
- Diện tích toàn phần của hình lập phương = diện tích một mặt nhân với \(6\).
Lời giải chi tiết:
a) Chu vi đáy của hình hộp chữ nhật là:
\((8,5 + 5,2) \times 2 = 27,4\,\,(cm)\)
Diện tích xung quanh của hình hộp chữ nhật là:
\(27,4 \times 4 = 109,6\,\,(c{m^2})\)
Diện tích đáy của hình hộp chữ nhật là:
\(8,5 \times 5,2 = 44,2\,\,(c{m^2})\)
Diện tích toàn phần của hình hộp chữ nhật là:
\(109,6 + 44,2 \times 2 = 198\,\,(c{m^2})\)
b) Diện tích một mặt của hình lập phương đó là:
\(4 \times 4 = 16\,\,(c{m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(16 \times 4 = 64\,\,(c{m^2})\)
Diện tích toàn phần của hình lập phương đó là:
\(16 \times 6 = 96\,\,(c{m^2})\)
Bài 5
Tính diện tích xung quanh và diện tích toàn phần của :
a) Hình hộp chữ nhật có chiều dài 1,8m; chiều rộng 1,2m ; chiều cao 1,5m.
b) Hình lập phương cạnh 32,5dm.
Phương pháp giải:
- Diện tích xung quanh của hình hộp chữ nhật = (chiều dài + chiều rộng) x 2 x chiều cao.
- Diện tích toàn phần của hình hộp chữ nhật = Diện tích xung quanh + diện tích 2 mặt hai đáy.
- Diện tích xung quanh của hình lập phương = diện tích một mặt nhân với \(4\).
- Diện tích toàn phần của hình lập phương = diện tích một mặt nhân với \(6\).
Lời giải chi tiết:
a) Chu vi đáy của hình hộp chữ nhật là:
\((1,8 + 1,2) \times 2 = 6\,\,(m)\)
Diện tích xung quanh của hình hộp chữ nhật là:
\(6 \times 1,5 = 9\,\,({m^2})\)
Diện tích đáy của hình hộp chữ nhật là:
\(1,8 \times 1,2 = 2,16\,\,({m^2})\)
Diện tích toàn phần của hình hộp chữ nhật là:
\(9 + 2,16 \times 2 = 13,32\,\,({m^2})\)
b) Diện tích một mặt của hình lập phương đó là:
\(32,5 \times 32,5 = 1056,25\,\,(d{m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(1056,25 \times 4 = 4225\,\,(d{m^2})\)
Diện tích toàn phần của hình lập phương đó là:
\(1056,25 \times 6 = 6337,5\,\,(d{m^2})\)
Bài 6
Người ta làm một cái thùng dạng hình hộp chữ nhật không nắp bằng tôn có chiều cao 80dm, chiều rộng 40dm, chiều dài 60dm. Tính diện tích tôn để làm cái thùng đó (không kể mép hàn).
Phương pháp giải:
Vì thùng tôn không có nắp nên thùng tôn đó có \(1\) mặt đáy và \(4\) mặt bên.
- Tính diện tích xung quanh của thùng tôn = chu vi đáy nhân với chiều cao.
- Tính diện tích đáy của thùng tôn = chiều dài x chiều rộng.
- Diện tích tôn dùng để làm cái thùng = diện tích xung quanh của thùng + diện tích 1 mặt đáy.
Lời giải chi tiết:
Diện tích xung quanh của thùng tôn đó là:
\((60 + 40) \times 2 \times 80 = 16000\,\,(d{m^2})\)
Diện tích đáy của thùng tôn đó là:
\(60 \times 40 = 2400\,\,(d{m^2})\)
Diện tích tôn dùng để làm thùng là:
\(16000 + 2400 = 18400\,\,(d{m^2})\)
Đáp số: \(18400d{m^2}\).
Lưu ý khi giải: Một số học sinh không đọc kĩ đề nên tính diện tích tôn để làm thùng chính bằng diện tích toàn phần của hình hộp chữ nhật.
Bài 7
Các hình dưới đây đều được tạo bởi các hình lập phương nhỏ cạnh bằng 1cm:


Viết tiếp vào chỗ chấm cho thích hợp:
Hình A gồm ……. hình lập phương nhỏ, thể tích hình A là …….
Hình B gồm ……. hình lập phương nhỏ, thể tích hình B là …….
Thể tích hình A ……. thể tích hình B.
Phương pháp giải:
- Mỗi hình lập phương nhỏ cạnh \(1cm\) có thể tích là \(1c{m^3}\).
- Đếm số hình vuông nhỏ của mỗi hình rồi tính thể tích của các hình đó.
Lời giải chi tiết:
Mỗi hình lập phương nhỏ cạnh \(1cm\) có thể tích là \(1c{m^3}\).
Hình A gồm \(7\) hình lập phương nhỏ, thể tích hình A là \(7c{m^3}\).
Hình B gồm \(7\) hình lập phương nhỏ, thể tích hình B là \(7c{m^3}\).
Thể tích hình A bằng thể tích hình B.
Bài 8
Mỗi hình dưới đây được xếp bởi các hình lập phương nhỏ cạnh 1cm:
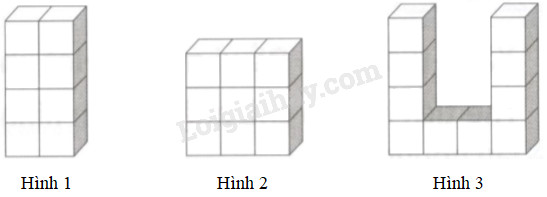
Viết vào chỗ chấm cho thích hợp:
Hình có thể tích bé nhất là hình ……. Hình có thể tích lớn nhất là hình …….
Phương pháp giải:
- Mỗi hình lập phương nhỏ cạnh \(1cm\)có thể tích là \(1c{m^3}\).
- Đếm số hình vuông nhỏ của mỗi hình rồi tính thể tích của các hình đó.
- So sánh thể tích của các hình để tìm hình có thể tích lớn nhất, hình có thể tích nhỏ nhất.
Lời giải chi tiết:
Mỗi hình lập phương nhỏ cạnh \(1cm\) có thể tích là \(1c{m^3}\).
Hình 1 gồm \(8\) hình lập phương nhỏ, thể tích hình 1 là \(8c{m^3}\).
Hình 2 gồm \(9\) hình lập phương nhỏ, thể tích hình 2 là \(9c{m^3}\).
Hình 3 gồm \(10\) hình lập phương nhỏ, thể tích hình 3 là \(10c{m^3}\).
Mà: \(8c{m^3} < 9c{m^3} < 10c{m^3}\)
Vậy hình có thể tích bé nhất là hình 1. Hình có thể tích lớn nhất là hình 3.
Vui học
Bác Thanh muốn làm một chiếc tủ kính hình hộp chữ nhật có kích thước như hình vẽ bên để treo quần áo. Em hãy giúp bác Thanh tính diện tích kính dùng làm chiếc tủ đó.
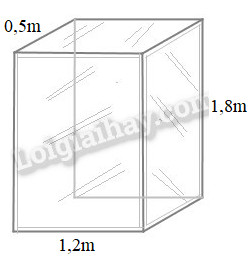
Phương pháp giải:
Chiếc tủ kính hình hộp chữ nhật đã cho có với chiều dài 1,2m, chiều rộng 50cm, chiều cao 1,8m.
Diện tích kính dùng để làm chiếc tủ đó chính là diện tích toàn phần của cái tủ hình hộp chữ nhật đó.
Để giải ta có thể thực hiện các bước như sau:
- Tính chu vi đáy theo công thức: chu vi đáy = (chiều dài + chiều rộng) \( \times \,2\).
- Tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi đáy nhân với chiều cao
- Tính diện tích đáy ta lấy chiều dài nhân với chiều rộng.
- Tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Lời giải chi tiết:
Chu vi đáy của chiếc tủ kính đó là:
\((1,2 + 0,5) \times 2 = 3,4\,\,(m)\)
Diện tích xung quanh của chiếc tủ kính đó là:
\(3,4 \times 1,8 = 6,12\,\,({m^2})\)
Diện tích đáy của chiếc tủ kính đó là:
\(1,2 \times 0,5 = 0,6\,\,({m^2})\)
Diện tích toàn phần của chiếc tủ kính đó là:
\(6,12 + 0,6 \times 2 = 7,32\,\,({m^2})\)
Vì diện tích toàn phần của chiếc tủ chính bằng diện tích kính dùng để làm cái hộp nên diện tích kính dùng để làm chiếc tủ đó là \(7,32{m^2}\).
Đáp số: \(7,32{m^2}\).
Loigiaihay.com
- Tuần 23: Xăng-ti-mét khối. Đề-xi-mét khối. Mét khối. Thể tích hình hộp chữ nhật. Thể tích hình lập phương - trang 22
- Tuần 24: Giới thiệu hình trụ. Giới thiệu hình cầu. Luyện tập chung - trang 26
- Kiểm tra giữa học kì II
- Tuần 25: Bảng đơn vị đo thời gian. Cộng, trừ số đo thời gian - trang 32
- Tuần 26: Nhân số đo thời gian với một số. Chia số đo thời gian cho một số. Vận tốc - trang 35
>> Xem thêm
Các bài khác cùng chuyên mục
- Kiểm tra cuối học kì 1 trang 65
- Tuần 18: Diện tích hình tam giác trang 61
- Tuần 17: Luyện tập chung. Sử dụng máy tính bỏ túi để giải toán về tỉ số phần trăm. Hình tam giác trang 57
- Tuần 16: Giải toán về tỉ số phần trăm (tiếp theo)
- Tuần 15: Luyện tập chung. Tỉ số phần trăm. Giải toán về tỉ số phần trăm trang 51
- Kiểm tra cuối học kì 1 trang 65
- Tuần 18: Diện tích hình tam giác trang 61
- Tuần 17: Luyện tập chung. Sử dụng máy tính bỏ túi để giải toán về tỉ số phần trăm. Hình tam giác trang 57
- Tuần 16: Giải toán về tỉ số phần trăm (tiếp theo)
- Tuần 15: Luyện tập chung. Tỉ số phần trăm. Giải toán về tỉ số phần trăm trang 51













Danh sách bình luận