Giải mục 2 trang 28, 29 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ2

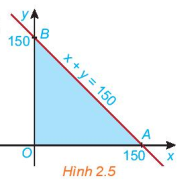
Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.

a) Xác định miền nghiệm \({D_1},{D_2},{D_3}\) của các bất phương trình tương ứng \(x \ge 0;y \ge 0\) và \(x + y \le 150\).

b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\) hay không?

c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:

\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Phương pháp giải:

a) Biểu diễn các miền nghiệm của từng bất phương trình \(x \ge 0;y \ge 0\) và \(x + y \le 150\)

Bước 1: Vẽ đường thẳng (nét liền) \(ax + by = c\).

Bước 2: Lấy điểm một điểm không thuộc đường thẳng \(ax + by = c\) và thay vào bất phương trình cần xác định miền nghiệm.

Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.

b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.

Lời giải chi tiết:

a)

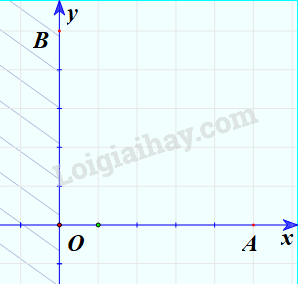
Miền nghiệm của bất phương trình \(x \ge 0\)

Bước 1: Vẽ đường thẳng (nét liền) \(x = 0\). Đây là trục Oy.

Bước 2: Lấy điểm A(150;0) không thuộc trục Oy và thay vào biểu thức \(x\), ta được: \(x = 150 \ge 0\).

Bước 3: Do điểm A thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm A.

Minh họa (phần không bị gạch chéo):

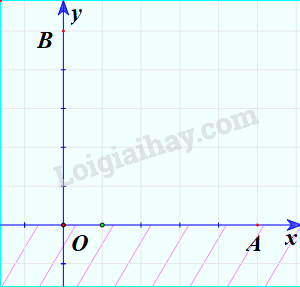
Miền nghiệm của bất phương trình \(y \ge 0\)

Bước 1: Vẽ đường thẳng (nét liền) \(y = 0\). Đây là trục Ox.

Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức \(y\), ta được: \(y = 150 \ge 0\).

Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.

Minh họa (phần không bị gạch chéo):

Miền nghiệm của bất phương trình \(x + y \le 150\):

Bước 1: Vẽ đường thẳng (nét liền) \(x + y = 150\).

Bước 2: Lấy điểm O(0;0) không thuộc đường thẳng \(x + y = 150\) và thay vào \(x + y\), ta được: \(0 + 0 = 0 \le 150\)

Bước 3: Do điểm O thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm O.

Minh họa (phần không bị gạch chéo):

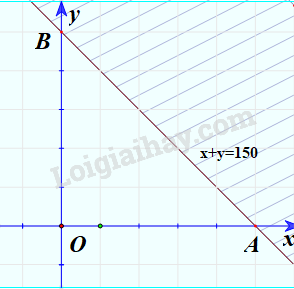
Vậy \({D_1}\) là nửa trên mặt phẳng có bờ là trục Oy, \({D_2}\) là nửa bên phải mặt phẳng có bờ là trục Ox và \({D_3}\) là nửa mặt phẳng có bờ là đường thẳng x+y=150 chứa điểm O.

b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.

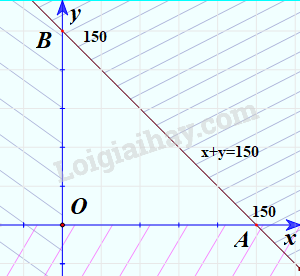
=>Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\)

c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:

\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Lấy điểm (1;2) trong tam giác OAB, thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Ta được:

\(\left\{ {\begin{array}{*{20}{l}}
{1 \ge 0}\\
{2 \ge 0}\\
{1 + 2 \le 150}
\end{array}} \right.\) (luôn đúng)

Vậy điểm (1;2) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Lấy điểm (1;149), thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Ta được: 

\(\left\{ {\begin{array}{*{20}{l}}
{1 \ge 0}\\
{149 \ge 0}\\
{1 + 149 \le 150}
\end{array}} \right.\) (luôn đúng)

Vậy điểm (1;149) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

LT 2

Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:  \(\left\{ \begin{array}{l}x \ge 0\\y > 0\\x + y \le 100\\2x + y < 120\end{array} \right.\)

Phương pháp giải:

Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)

Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)

Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)

Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)

Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Lời giải chi tiết:

Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)

Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0).

Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)

Miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) không kể trục Ox.

Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)

+ Vẽ đường thẳng d: x+y=100

+ Vì 0+0=0

Do đó, miền nghiệm của bất phương trình \(x + y \le 100\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.

Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)

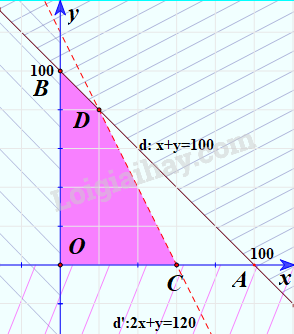
Tương tự miền nghiệm của bất phương trình \(2x + y < 120\) là nửa mặt phẳng bờ d’ chúa gốc tọa độ O. (không kể đường thẳng d’).

Khi đó miền không bị gạch là giao của các miền nghiệm của các bất phương trình trong hệ. Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không kể đoạn thẳng OC và CD).