Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức

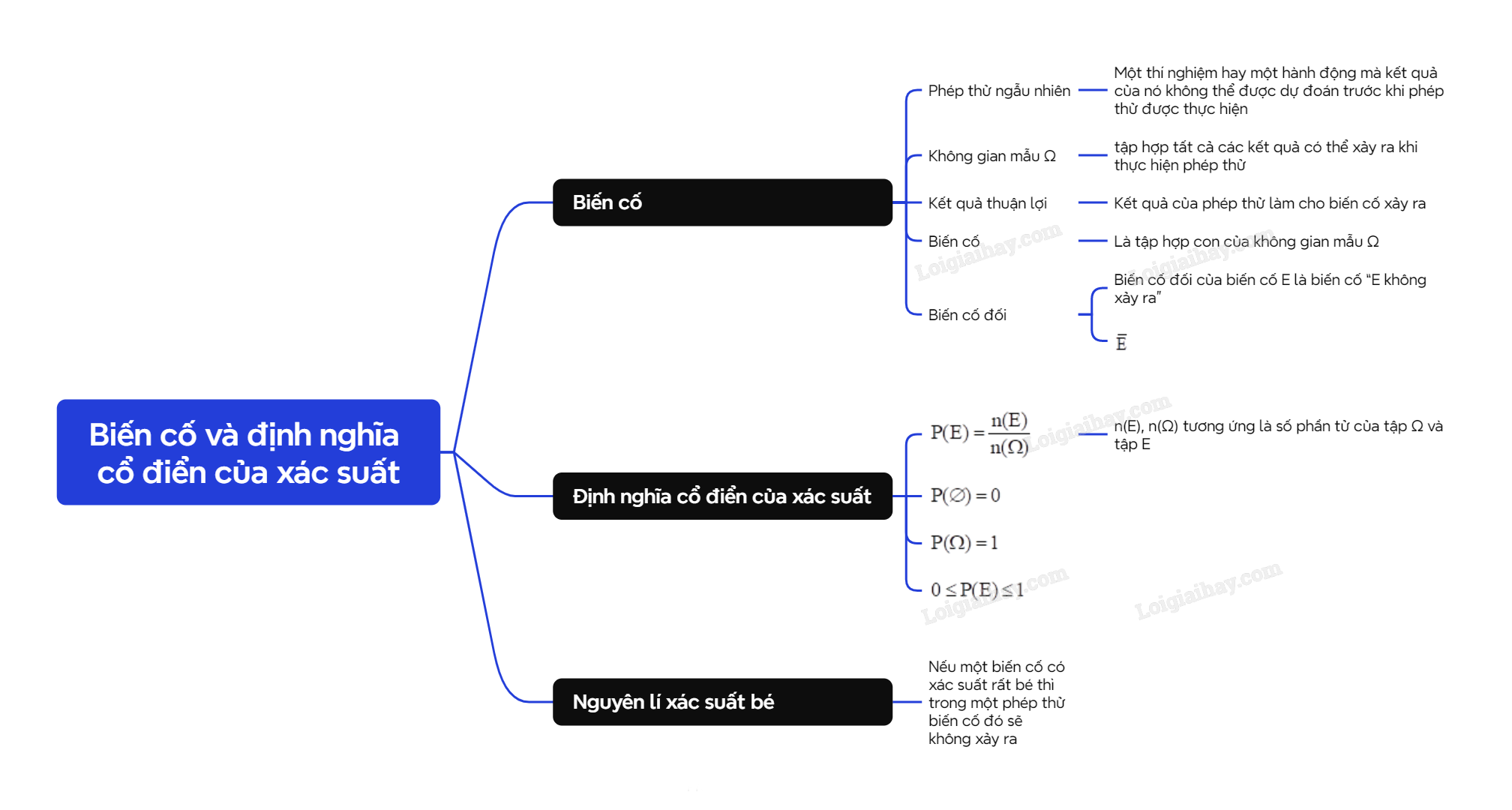
A. Lý thuyết

1. Biến cố

Chú ý: Ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn kết quả.

Nhận xét: Biến cố chắc chắn là tập Ω, biến cố không thể là tập ∅.

Nhận xét: Nếu biến cố E là tập con của không gian mẫu Ω thì biến cố đối \(\overline E \) là tập hợp tất cả các phần tử của Ω mà không là phần tử của E. Vậy biến cố \(\overline E \) là phần bù của E trong Ω: \(\overline E  = {C_\Omega }E\).

2. Định nghĩa cổ điển của xác suất

Một cách tổng quát, ta có định nghĩa sau:

Xét phép thử chỉ có một số hữu hạn kết quả có thể xảy ra và khả năng xảy ra của từng kết quả là giống nhau. Gọi Ω là không gian mẫu của phép thử đó. Khi đó, với mỗi biến cố A, ta có định nghĩa cổ điển của xác suất như sau:

Nhận xét:

+ \(P(\emptyset ) = 0\); \(P(\Omega ) = 1\).

+ \(0 \le P(E) \le 1\) với mỗi biến cố E.

3. Nguyên lí xác suất bé

Nếu một biến cố có xác suất rất bé thì trong một phép thử biến cố đó sẽ không xảy ra.

Tuy nhiên, một xác suất như thế nào được xem là bé phụ thuộc vào từng bài toán cụ thể.

B. Bài tập

Bài 1: Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên một quả bóng từ trong hộp, ghi lại màu của quả bóng được lấy ra và bỏ lại quả bóng đó vào hộp. Xét phép thử “Lấy ngẫu nhiên tiếp 2 quả bóng trong hộp”. Hãy cho biết không gian mẫu của phép thử đó.

Giải:

Không gian mẫu của phép thử trên là tập hợp Ω = {XX; XD; XV; ĐD; ĐV; DX; DV; VX; VD}, ở đó, chẳng hạn XD là kết quả “Lần thứ nhất lấy ra quả bóng xanh, lần thứ hai lấy ra quả bóng đỏ”.

Bài 2: Gieo một đồng xu cản đối liên tiếp ba lần. Gọi E là biến cố: “Có hai lần xuất hiện mặt sấp và một lần xuất hiện mặt ngửa". Tính xác suất của biến cố E.

Giải:

Kí hiệu S và N tương ứng là đồng xu ra mặt sấp và đồng xu ra mặt ngửa.
Không gian mẫu Ω = {SSN; SNS; SNN; SSS; NSN; NNS; NNN; NSS}.
E = {SSN; SNS; NSS}.

Ta có n(Ω) = 8; n(E) = 3. Do đồng xu cân đối nên các kết quả có thể là đồng khả năng.

Vậy \(P(E) = \frac{{n(E)}}{{n(\Omega )}}\).

Bài 3: Gieo một con xúc xắc 6 mặt và quan sát số chấm xuất hiện trên con xúc xắc.

a) Mô tả không gian mẫu.

b) Gọi M là biến cố: “Số chấm xuất hiện trên con xúc xắc là một số chẵn". Nội dung biến cố đối M của M là gì?

c) Các biến cố M và \(\overline M \) là tập con nào của không gian mẫu?

Giải:

a) Không gian mẫu Ω = {1; 2; 3; 4; 5; 6}.

b) Biến cố đối M của M là biến cố: “Số chấm xuất hiện trên con xúc xắc là một số lẻ”.

c) Ta có \(M = \{ 2;4;6\}  \subset \Omega \); \(\overline M  = {C_\Omega }M = \{ 1;3;5\}  \subset \Omega \).