Giải bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều

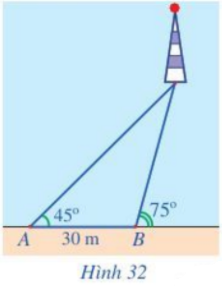
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75

Đề bài

Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là \({45^o}\) và \({75^o}\). Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Phương pháp giải - Xem chi tiết

Gọi C là vị trí ngọn hải đăng, H là hình chiếu của C trên AB.

Bước 1: Tính góc ACB, ABC.

Bước 2: Tính AC bằng cách áp dụng định lí sin trong tam giác ABC: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)

Bước 3: Tính AH bằng công thức: AH = AC. cos A.

Lời giải chi tiết

Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.

Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

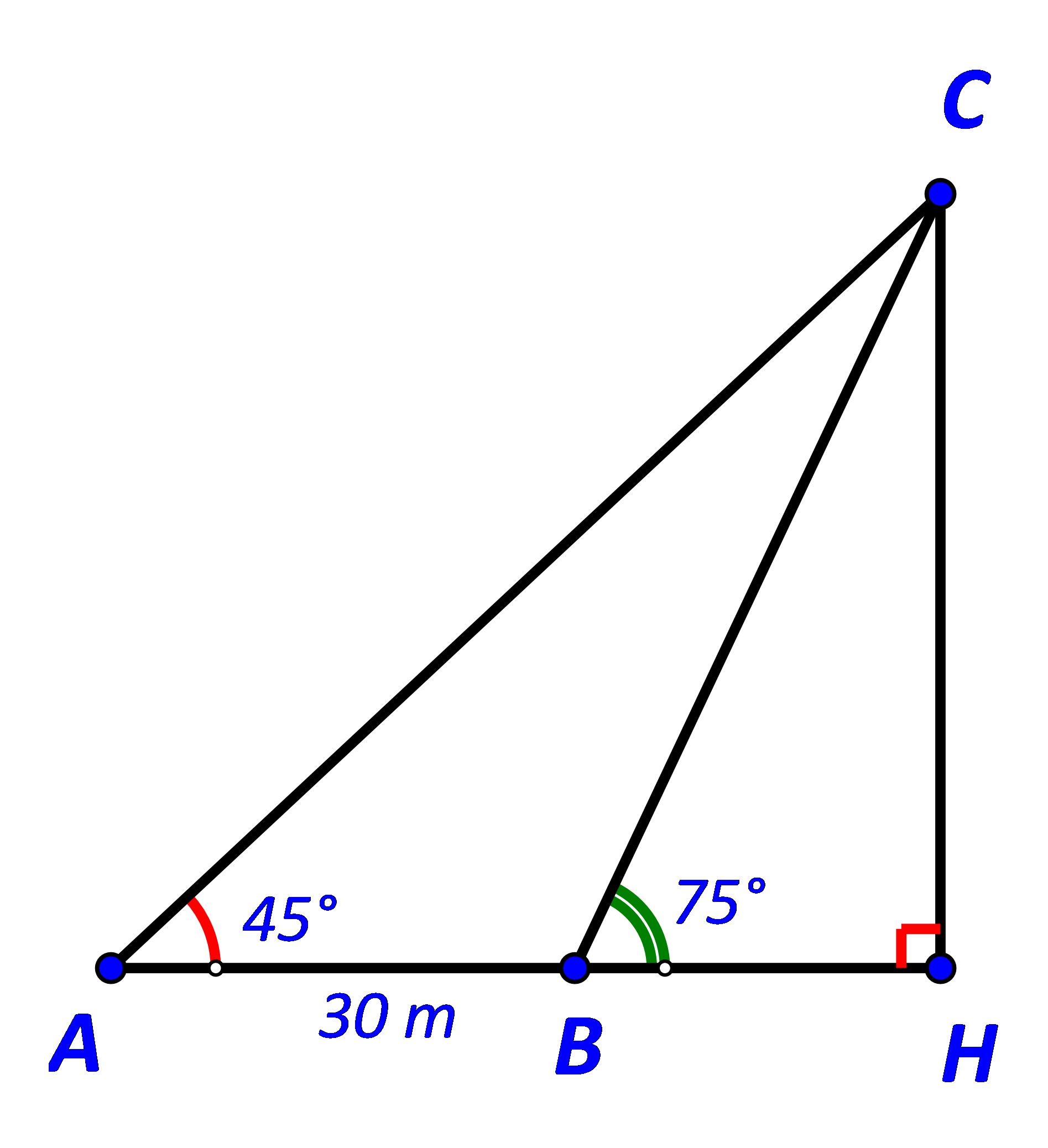
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)

Áp dụng định lí sin trong tam giác ABC ta có:

\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)

\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)

Tam giác ACH vuông tại H nên ta có:

\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)

Vậy ngọn hải đăng cách bờ biển 41 m.

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 16 phiếu

Bài tiếp theo

Giải bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB.
Giải bài 5 trang 77 SGK Toán 10 tập 1 – Cánh diều
Tính độ dài cạnh AB trong mỗi trường hợp sau:
Giải bài 4 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có AB = 12,AC = 15,BC = 20. Tính: a) Số đo các góc A, B, C. b) Diện tích tam giác ABC.
Giải bài 3 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có AB = 100, B = 100, C = 45 Tính: a) Độ dài các cạnh AC, BC b) Diện tích tam giác ABC.
Giải bài 2 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có AB = 5,BC = 7, A = 120 Tính độ dài cạnh AC.
Giải bài 1 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có BC = 12,CA = 15,C = 120 Tính: a) Độ dài cạnh AB. b) Số đo các góc A, B. c) Diện tích tam giác ABC.
Giải mục III trang 75, 76 SGK Toán 10 tập 1 - Cánh diều
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là
Giải mục II trang 73, 74, 75 SGK Toán 10 tập 1 - Cánh diều
Cho tam giác ABC có AB = 12; B = 60; C = 45. Tính diện tích của tam giác ABC. Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
Giải mục I trang 72, 73 SGK Toán 10 tập 1 - Cánh diều
Cho tam giác ABC có AB = c, Ac = b, BC = a. Viết công thức tính cos A. Viết công thức định lí sin cho tam giác ABC.
Giải câu hỏi khởi động trang 72 SGK Toán 10 tập 1 - Cánh diều
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau: