-
GIẢI SGK TOÁN 11 CÁNH DIỀU - MỚI NHẤT
-
Toán 10 tập 1 - Cánh diều
-
Toán 10 tập 2 - Cánh diều
Giải bài 3 trang 77 SGK Toán 10 tập 1 – Cánh diều
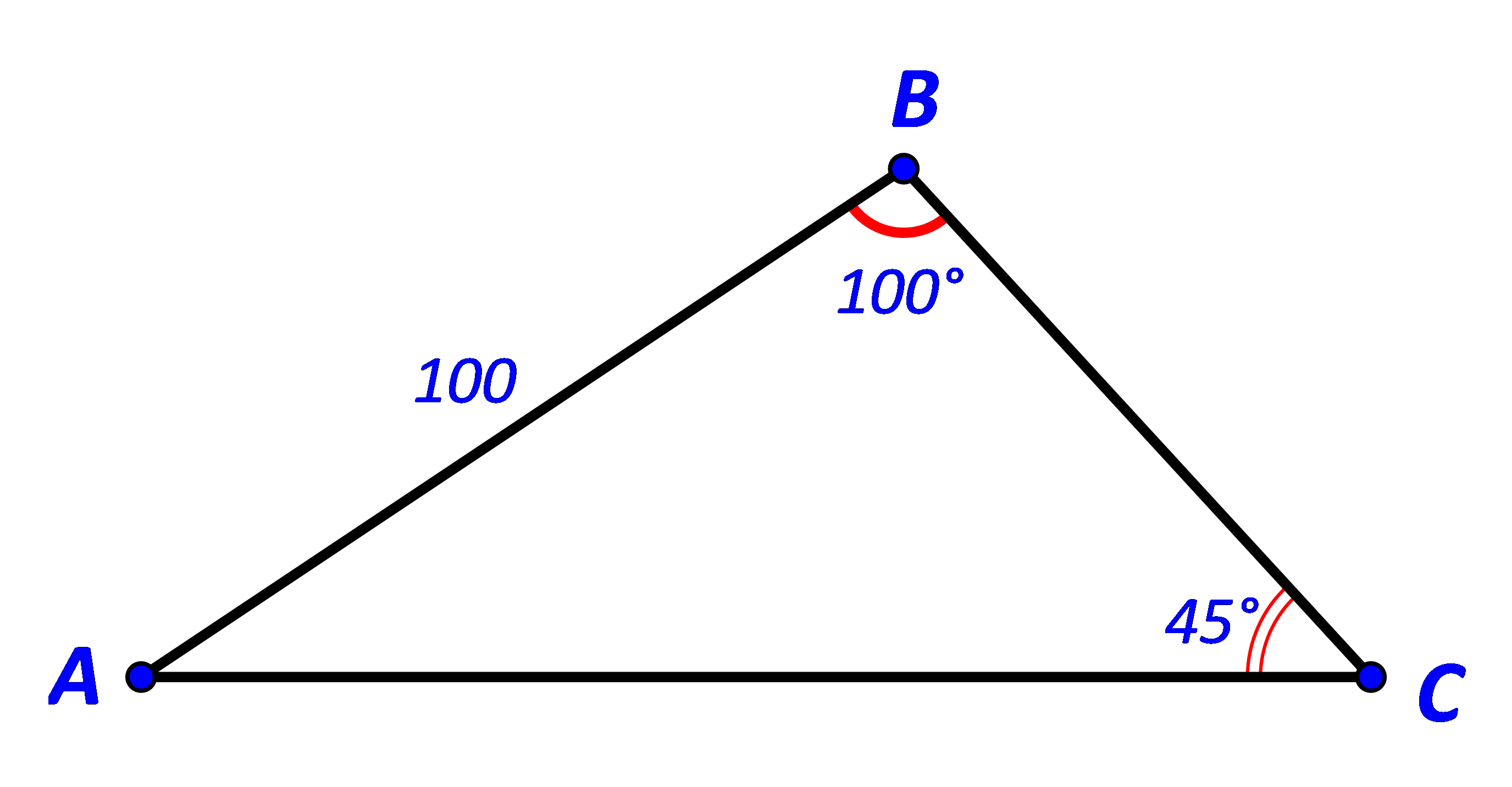
Cho tam giác ABC có AB = 100, B = 100, C = 45 Tính: a) Độ dài các cạnh AC, BC b) Diện tích tam giác ABC.
Đề bài
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
Phương pháp giải - Xem chi tiết
a)
Bước 1: Tính \(\widehat A\).
Bước 2: Tính AC, BC bằng cách áp dụng định lí sin trong tam giác ABC:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
b)
Tính diện tích tam giác ABC bằng một trong 4 công thức sau:
+) \(S = \frac{1}{2}.bc.\sin A = \frac{1}{2}.ac.\sin B = \frac{1}{2}.ab.\sin C\)
+) \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Lời giải chi tiết
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
Bình luận
Chia sẻ
- Giải bài 4 trang 77 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 5 trang 77 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 2 trang 77 SGK Toán 10 tập 1 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
