Giải bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều

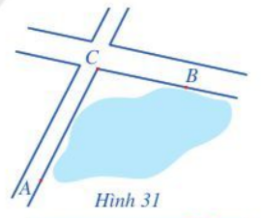
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB.

Đề bài

Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và \(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).

Phương pháp giải - Xem chi tiết

Bước 1: Đổi độ dài AC, CB về cùng đơn vị mét.

Bước 2: Tính AB: Áp dụng định lí cosin trong tam giác BAC: \(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)

Lời giải chi tiết

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.

Áp dụng định lí cosin trong tam giác ABC ta có:

\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)

\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)

Vậy khoảng cách AB là 1433,2 m.

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75
Giải bài 5 trang 77 SGK Toán 10 tập 1 – Cánh diều
Tính độ dài cạnh AB trong mỗi trường hợp sau:
Giải bài 4 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có AB = 12,AC = 15,BC = 20. Tính: a) Số đo các góc A, B, C. b) Diện tích tam giác ABC.
Giải bài 3 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có AB = 100, B = 100, C = 45 Tính: a) Độ dài các cạnh AC, BC b) Diện tích tam giác ABC.
Giải bài 2 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có AB = 5,BC = 7, A = 120 Tính độ dài cạnh AC.
Giải bài 1 trang 77 SGK Toán 10 tập 1 – Cánh diều
Cho tam giác ABC có BC = 12,CA = 15,C = 120 Tính: a) Độ dài cạnh AB. b) Số đo các góc A, B. c) Diện tích tam giác ABC.
Giải mục III trang 75, 76 SGK Toán 10 tập 1 - Cánh diều
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là
Giải mục II trang 73, 74, 75 SGK Toán 10 tập 1 - Cánh diều
Cho tam giác ABC có AB = 12; B = 60; C = 45. Tính diện tích của tam giác ABC. Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
Giải mục I trang 72, 73 SGK Toán 10 tập 1 - Cánh diều
Cho tam giác ABC có AB = c, Ac = b, BC = a. Viết công thức tính cos A. Viết công thức định lí sin cho tam giác ABC.
Giải câu hỏi khởi động trang 72 SGK Toán 10 tập 1 - Cánh diều
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau: