Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc..

Giải bài 3.7 trang 37 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Cho góc bẹt xOy. Vẽ tia Oz sao cho

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat {xOz} = {60^0}\). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.

a)Tính số đo góc xOm.

b) Tính số đo góc yOn.

c) Tính số đo góc mOn.

Phương pháp giải - Xem chi tiết

a) Tia Om là tia phân giác của góc xOz

b) \(\widehat {yOz} + \widehat {zOx} = {180^0}\)

Tia On là tia phân giác của góc yOn

c) \(\widehat {xOm} + \widehat {mOy} = {180^0}\)

Tia On nằm giữa hai tia Oy và Om

Lời giải chi tiết

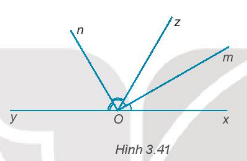
a) Vì tia Om là tia phân giác của góc xOz nên \(\widehat {xOm} = \widehat {mOz} = \dfrac{{\widehat {xOz}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\)

Vậy \(\widehat {xOm} = {30^0}\).

b) Ta có: \(\widehat {yOz} + \widehat {zOx} = {180^0}\) (hai góc kề bù)

\( \widehat {yOz} + {60^0} = {180^0}\)

nên \(\widehat {yOz} = {180^0} - {60^0} = {120^0}\)

Vì tia On là tia phân giác của góc yOn nên \(\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\)

c) Ta có: \(\widehat {xOm} + \widehat {mOy} = {180^0}\) (hai góc kề bù)

\( {30^0} + \widehat {mOy} = {180^0}\)

nên \(\widehat {mOy} = {180^0} - {30^0} = {150^0}\)

Tia On nằm giữa hai tia Oy và Om nên \(\widehat {yOn} + \widehat {nOm} = \widehat {yOm}\)

\({60^0} + \widehat {nOm} = {150^0}\)

suy ra \(\widehat {nOm} = {150^0} - {60^0} = {90^0}\)

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 22 phiếu

>> Xem thêm

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE