Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc..

Giải bài 3.3 trang 37 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho \(\widehat {xOm} = {120^\circ }\). Tính các góc mOy, yOn, xOn.

Phương pháp giải - Xem chi tiết

-Hai góc đối đỉnh thì bằng nhau

- Hai góc kề bù có tổng bằng 180 độ

Lời giải chi tiết

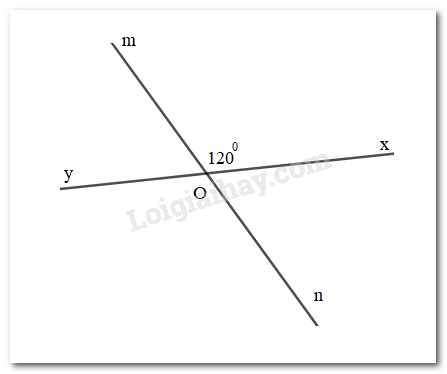
Ta có: \(\widehat {yOm} + \widehat {mOx} = {180^\circ}\) (hai góc kề bù)

\(\begin{array}{l} \widehat {yOm} + {120^\circ} = {180^\circ}\\ \text{suy ra }\widehat {yOm} = {180^\circ} - {120^\circ} = {60^\circ}\end{array}\)

Lại có: \(\widehat {mOy} + \widehat {yOn} = {180^\circ}\) (hai góc kề bù)

\(\begin{array}{l} {60^\circ} + \widehat {yOn} = {180^\circ}\\ \text{suy ra }\widehat {yOn} = {180^\circ} - {60^\circ} = {120^\circ}\end{array}\)

Mặt khác: \(\widehat {xOn} = \widehat {yOm} = {60^\circ}\) (hai góc đối đỉnh)

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 22 phiếu

>> Xem thêm

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE