-
GIẢI SGK TOÁN 8 CÁNH DIỀU - MỚI NHẤT
-
Toán 7 tập 1 - Cánh diều
-
Chương I. Số hữu tỉ
-
Chương II. Số thực
- Bài 1. Số vô tỉ. Căn bậc hai số học
- Bài 2. Tập hợp R các số thực
- Bài 3. Giá trị tuyệt đối của một số thực
- Bài 4. Làm tròn và ước lượng
- Bài 5. Tỉ lệ thức
- Bài 6. Dãy tỉ số bằng nhau
- Bài 7. Đại lượng tỉ lệ thuận
- Bài 8. Đại lượng tỉ lệ nghịch
- Bài tập cuối chương II
- Hoạt động thực hành và trải nghiệm. Chủ đề 1: Một số hình thức khuyến mãi trong kinh doanh
-
Chương III. Hình học trực quan
-
Chương IV. Góc. Đường thẳng song song
-
-
Toán 7 tập 2 - Cánh diều
-
Chương V. Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập, phân loại và biểu diễn dữ liệu
- Bài 2. Phân tích và xử lí dữ liệu
- Bài 3. Biểu đồ đoạn thẳng
- Bài 4. Biểu đồ hình quạt tròn
- Bài 5. Biến cố trong một số trò chơi đơn giản
- Bài 6. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài tập cuối chương V
- Hoạt động thực hành và trải nghiệm. Chủ đề 3. Dung tích phổi
-
Chương VI. Biểu thức đại số
-
Chương VII. Tam giác
- Bài 1. Tổng các góc của một tam giác
- Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
- Bài 3. Hai tam giác bằng nhau
- Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
- Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
- Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc
- Bài 7. Tam giác cân
- Bài 8. Đường vuông góc và đường xiên
- Bài 9. Đường trung trực của một đoạn thẳng
- Bài 10. Tính chất ba đường trung tuyến của tam giác
- Bài 11. Tính chất ba đường phân giác của tam giác
- Bài 12. Tính chất ba đường trung trực của tam giác
- Bài 13. Tính chất ba đường cao của tam giác
- Bài tập cuối chương VII
-
Giải bài 3 trang 79 SGK Toán 7 tập 2 - Cánh diều
Cho
Tổng hợp đề thi giữa kì 2 lớp 7 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN...
Đề bài
Cho \(\Delta ABC = \Delta MNP\) và \(\widehat A + \widehat N = 125^\circ \). Tính số đo góc P.
Phương pháp giải - Xem chi tiết
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.
Tổng ba góc trong một tam giác bằng 180°.
Lời giải chi tiết
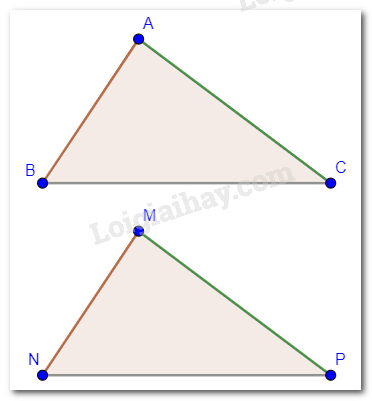
Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.
Bình luận
Chia sẻ
- Giải bài 4 trang 79 SGK Toán 7 tập 2 - Cánh diều
- Lý thuyết Hai tam giác bằng nhau SGK Toán 7 - Cánh diều
- Giải bài 2 trang 79 SGK Toán 7 tập 2 - Cánh diều
- Giải bài 1 trang 79 SGK Toán 7 tập 2 - Cánh diều
- Giải câu hỏi trang 78, 79 SGK Toán 7 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Tạo đồ dùng dạng hình lăng trụ đứng SGK Toán 7 Cánh diều tập 1
- Giải câu hỏi trang 39, 40 SGK Toán 7 Cánh diều tập 2
- Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều
- Tạo đồ dùng dạng hình lăng trụ đứng SGK Toán 7 Cánh diều tập 1
- Giải câu hỏi trang 39, 40 SGK Toán 7 Cánh diều tập 2
- Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều
Danh sách bình luận