-
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
-
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Giải bài 1 trang 100 sách bài tập toán 10 - Chân trời sáng tạo
Cho tam giác vuông cân ABC có AB = AC = a
Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Cho tam giác vuông cân ABC có \(AB = AC = a\).
Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} \)
Lời giải chi tiết
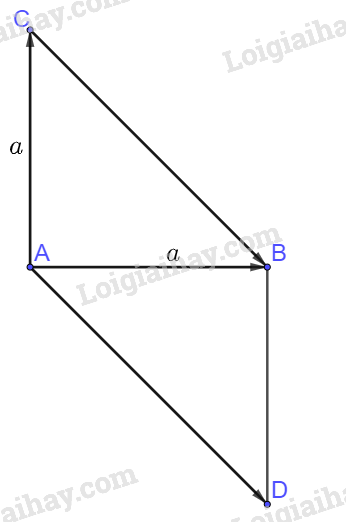
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right) = a.a.\cos 90^\circ = 0\)
Từ A kẻ \(\overrightarrow {AD} = \overrightarrow {CB} \Rightarrow \widehat {CAD} = 135^\circ ;AD = BC = a\sqrt 2 \), ta có:
\(\overrightarrow {AC} .\overrightarrow {CB} = \overrightarrow {AC} .\overrightarrow {AD} = AC.CB.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AD} } \right) = a.a\sqrt 2 .\cos 135^\circ = - {a^2}\)
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí
