Đề thi học kì 1 Toán 11 Kết nối tri thức - Đề số 3
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng
Đề bài
Xét góc lượng giác \(\left( {OA,OM} \right) = \alpha \), trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó, M thuộc góc phần tư nào để \(\sin \alpha \) và \(\cos \alpha \) trái dấu?
-
A.
Góc phần tư thứ (I) và (II).
-
B.
Góc phần tư thứ (I) và (III).
-
C.
Góc phần tư thứ (II) và (IV).
-
D.
Góc phần tư thứ (II) và (III).
Cho \({90^0} < \alpha < {180^0}\). Chọn khẳng định đúng:
-
A.
\(\sin \alpha > 0\).
-
B.
\(\cos \alpha > 0\).
-
C.
\(\tan \alpha > 0\).
-
D.
\(\cot \alpha > 0\).
Trong các giá trị sau, \(\sin \alpha \) không thể nhận giá trị nào?
-
A.
0,9.
-
B.
1,2.
-
C.
1.
-
D.
\( - 0,5\).
Chọn phát biểu đúng:
-
A.
Hàm số \(y = \cot x\) là hàm số chẵn.
-
B.
Hàm số \(y = \tan x\) là hàm số chẵn.
-
C.
Hàm số \(y = \sin x\) là hàm số chẵn.
-
D.
Hàm số \(y = \cos x\) là hàm số chẵn.
Tập xác định của hàm số \(y = 2\sin x\) là:
-
A.
\(\left[ { - 1;1} \right]\).
-
B.
\(\left( { - 1;1} \right)\).
-
C.
\(\mathbb{R}\).
-
D.
\(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Chọn khẳng định đúng:
-
A.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} - {u_n} < 0\) với mọi \(n \in \mathbb{N}*\).
-
B.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} - {u_n} > 0\) với mọi \(n \in \mathbb{N}*\).
-
C.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} + {u_n} < 0\) với mọi \(n \in \mathbb{N}*\).
-
D.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} + {u_n} > 0\) với mọi \(n \in \mathbb{N}*\)
Dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho 5. Số nào dưới đây thuộc dãy số \(\left( {{u_n}} \right)\)?
-
A.
1.
-
B.
3.
-
C.
5.
-
D.
7.
Cấp số cộng nào dưới đây có công sai bằng 3?
-
A.
1; 3; 5; 7; 9; 11; ...
-
B.
1; 3; 9; 27; …
-
C.
11; 8; 5; 2; …
-
D.
0; 3; 6; 9; …
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\). Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right)\)
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = 4\).
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = - 4\).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = 10\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = - 10\).
Phát biểu nào sau đây là sai?
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = c\) (c là hằng số).
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\left( {\left| q \right| > 1} \right)\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^k}}} = 0\left( {k > 1} \right)\).
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu:
-
A.
\(g\left( {{x_0}} \right) \ne 0\).
-
B.
\(f\left( {{x_0}} \right) \ne 0\).
-
C.
\(g\left( {{x_0}} \right) = 0\).
-
D.
\(f\left( {{x_0}} \right) = 0\).
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } {x^5}\) là:
-
A.
3.
-
B.
2.
-
C.
\( - 2\).
-
D.
\( + \infty \).
Một mặt phẳng được xác định nếu mặt phẳng đó chứa:
-
A.
Ba điểm phân biệt.
-
B.
Một đường thẳng và một điểm thuộc đường thẳng đó.
-
C.
Hai đường thẳng cắt nhau.
-
D.
Hai đường thẳng phân biệt.
Cho hình chóp S. ABCD với ABCD là hình bình hành. Hai điểm S và B cùng thuộc hai mặt phẳng:
-
A.
(SAC) và (SBD).
-
B.
(SAB) và (SBD).
-
C.
(SAB) và (SDC).
-
D.
A, B, C đều sai.
Trong các mệnh đề sau, mệnh đề nào đúng?
-
A.
Hai đường thẳng chéo nhau khi không có điểm chung.
-
B.
Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
-
C.
Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
-
D.
Hai đường thẳng song song khi và chỉ khi chúng ở trên cùng hai mặt phẳng.
Cho hình hộp ABCD. A’B’C’D’. Hình hộp đó có bao nhiêu mặt bên?
-
A.
6.
-
B.
5.
-
C.
4.
-
D.
3.
Khẳng định nào sau đây là sai?
-
A.
Hình lăng trụ có hai mặt đáy bằng nhau.
-
B.
Hình lăng trụ có các mặt bên là hình bình hành.
-
C.
Hình lăng trụ có các cạnh bên bằng nhau.
-
D.
Hình lăng trụ có các mặt bên bằng nhau.
Qua phép chiếu song song, tính chất nào không được bảo toàn?
-
A.
Đồng quy.
-
B.
Song song.
-
C.
Chéo nhau.
-
D.
Thẳng hàng.
Biết rằng \(\tan \alpha = 2\). Giá trị biểu thức \(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }}\) \(\left( {\cos \alpha \ne 0} \right)\)là:
-
A.
\(\frac{4}{5}\).
-
B.
1.
-
C.
\(\frac{3}{5}\).
-
D.
\(\frac{5}{3}\).
Cho tam giác ABC. Chọn đáp án đúng:
-
A.
\(\sin \frac{{A + B}}{2} = \cos \frac{C}{2}\).
-
B.
\(\sin \frac{{A + B}}{2} = - \sin \frac{C}{2}\).
-
C.
\(\sin \frac{{A + B}}{2} = - \cos \frac{C}{2}\).
-
D.
\(\sin \frac{{A + B}}{2} = \sin \frac{C}{2}\).
Tập xác định của hàm số \(y = \frac{{2\sin x}}{{\sin x - \cos x}}\) là:
-
A.
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
-
B.
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
-
C.
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
-
D.
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = \frac{{2n + 1}}{{n + 2}}\). Số \(\frac{{167}}{{84}}\) là số hạng thứ bao nhiêu của dãy số?
-
A.
240.
-
B.
250.
-
C.
260.
-
D.
270.
Cho \(\left( {{u_n}} \right)\) là cấp số cộng thỏa mãn \({u_2} = 8;{u_4} = 12\). Số hạng đầu của cấp số cộng bằng:
-
A.
6.
-
B.
4.
-
C.
2.
-
D.
Đáp án khác.
Tính tổng \(S = 1 + \frac{1}{2} + \frac{1}{4} + ... + \frac{1}{{{2^9}}}\)
-
A.
\(S = \frac{{1\;021}}{{511}}\).
-
B.
\(S = \frac{{1\;021}}{{512}}\).
-
C.
\(S = \frac{{1\;023}}{{511}}\).
-
D.
\(S = \frac{{1\;023}}{{512}}\).
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^4} - 2{x^2} - 1} \right)\) bằng:
-
A.
4.
-
B.
0.
-
C.
\( - \infty \).
-
D.
\( + \infty \).
Chọn đáp án đúng:
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \frac{1}{4}\).
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = 3\).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \frac{1}{3}\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \frac{1}{2}\).
Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{{{x^3} - x}}\). Kết luận nào sau đây là đúng?
-
A.
Hàm số liên tục tại \(x = - 1\).
-
B.
Hàm số liên tục tại \(x = 0\).
-
C.
Hàm số liên tục tại \(x = 1\).
-
D.
Hàm số liên tục tại \(x = \frac{1}{4}\).
Cho hình chóp tứ giác S. ABCD có BD và AC cắt nhau tại O. Trên SC lấy M không trùng với S và C, đường thẳng AM cắt SO tại K. Đường thẳng SD cắt đường thẳng nào?
-
A.
BC.
-
B.
BK.
-
C.
AC.
-
D.
AM.
Cho hình chóp S. ABCD có đáy là hình thang (AD// CB, \(BC < AD\)). Gọi M, N lần lượt là trung điểm của SA và SD. Khẳng định nào sau đây là đúng?
-
A.
MN//BC.
-
B.
MN\( \bot \)BC.
-
C.
MN cắt BC.
-
D.
Cả A, B, C đều sai.
Cho hình chóp S. ABCD có đáy ABCD là hình thang (AB//CD). Gọi O là giao điểm của AC và BD, I là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
-
A.
SI.
-
B.
SO.
-
C.
Đường thẳng qua S vuông góc với SI.
-
D.
Đường thẳng qua S song song với DC.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, G lần lượt là các điểm thuộc SB, SC sao cho \(\frac{{SM}}{{MB}} = \frac{{SG}}{{GC}} = 2\). Tứ giác MGDA là hình gì?
-
A.
Hình thoi.
-
B.
Hình bình hành.
-
C.
Hình thang.
-
D.
Hình chữ nhật.
Tứ phân vị \({Q_2}\) của mẫu số liệu ghép nhóm là:
-
A.
Trung vị của mẫu số liệu ghép nhóm.
-
B.
Trung bình của mẫu số liệu ghép nhóm.
-
C.
Mốt của mẫu số liệu ghép nhóm.
-
D.
Cả A, B, C đều sai.
Kết quả khảo sát cân nặng của 25 quả bơ ở một lô hàng cho trong bảng sau:

Nhóm \(\left[ {160;165} \right)\) có tần số là bao nhiêu?
-
A.
7.
-
B.
12.
-
C.
3.
-
D.
2.
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được cho ở trong bảng sau (đơn vị: Triệu đồng):

-
A.
7,7.
-
B.
8,7.
-
C.
7,5.
-
D.
8,5.
Mẫu số liệu ghép nhóm dưới đây là thời gian (phút) từ nhà đến nơi làm việc của các nhân viên một công ty như sau:

Tứ phân vị thứ nhất của mẫu số liệu này là:
-
A.
\(\frac{{1360}}{{37}}\) phút.
-
B.
\(\frac{{136}}{5}\) phút.
-
C.
\(\frac{{1365}}{{37}}\) phút.
-
D.
\(\frac{{137}}{5}\) phút.
Lời giải và đáp án
Xét góc lượng giác \(\left( {OA,OM} \right) = \alpha \), trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó, M thuộc góc phần tư nào để \(\sin \alpha \) và \(\cos \alpha \) trái dấu?
-
A.
Góc phần tư thứ (I) và (II).
-
B.
Góc phần tư thứ (I) và (III).
-
C.
Góc phần tư thứ (II) và (IV).
-
D.
Góc phần tư thứ (II) và (III).
Đáp án : C
Sử dụng kiến thức về dấu của các giá trị lượng giác.
Với \(\alpha \in \) góc phần tư thứ I thì: \(\sin \alpha > 0,\cos \alpha > 0\)
Với \(\alpha \in \) góc phần tư thứ II thì: \(\sin \alpha > 0,\cos \alpha < 0\)
Với \(\alpha \in \) góc phần tư thứ III thì: \(\sin \alpha < 0,\cos \alpha < 0\)
Với \(\alpha \in \) góc phần tư thứ IV thì: \(\sin \alpha < 0,\cos \alpha > 0\)
Ta có: Với \(\alpha \in \) góc phần tư thứ I thì: \(\sin \alpha > 0,\cos \alpha > 0\)
Với \(\alpha \in \) góc phần tư thứ II thì: \(\sin \alpha > 0,\cos \alpha < 0\)
Với \(\alpha \in \) góc phần tư thứ III thì: \(\sin \alpha < 0,\cos \alpha < 0\)
Với \(\alpha \in \) góc phần tư thứ IV thì: \(\sin \alpha < 0,\cos \alpha > 0\)
Do đó, M thuộc góc phần tư thứ (II) và (IV) thì \(\sin \alpha \) và \(\cos \alpha \) trái dấu.
Cho \({90^0} < \alpha < {180^0}\). Chọn khẳng định đúng:
-
A.
\(\sin \alpha > 0\).
-
B.
\(\cos \alpha > 0\).
-
C.
\(\tan \alpha > 0\).
-
D.
\(\cot \alpha > 0\).
Đáp án : A
Sử dụng kiến thức về dấu của giá trị lượng giác: Với \({90^0} < \alpha < {180^0}\) thì \(\sin \alpha > 0\), \(\cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0\).
Với \({90^0} < \alpha < {180^0}\) thì \(\sin \alpha > 0\), \(\cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0\).
Trong các giá trị sau, \(\sin \alpha \) không thể nhận giá trị nào?
-
A.
0,9.
-
B.
1,2.
-
C.
1.
-
D.
\( - 0,5\).
Đáp án : B
Sử dụng kiến thức về tập giá trị của hàm số \(y = \sin x\): \( - 1 \le \sin x \le 1\)
Vì \( - 1 \le \sin \alpha \le 1\) nên \(\sin \alpha \) không thể nhận giá trị 1,2.
Chọn phát biểu đúng:
-
A.
Hàm số \(y = \cot x\) là hàm số chẵn.
-
B.
Hàm số \(y = \tan x\) là hàm số chẵn.
-
C.
Hàm số \(y = \sin x\) là hàm số chẵn.
-
D.
Hàm số \(y = \cos x\) là hàm số chẵn.
Đáp án : D
Sử dụng kiến thức về hàm số chẵn: Hàm số \(y = f\left( x \right)\) với tập xác định D được gọi là hàm số chẵn nếu với mọi \(x \in D\) ta có \( - x \in D\) và \(f\left( { - x} \right) = f\left( x \right)\)
Vì \(\cos \left( { - x} \right) = \cos x\) nên hàm số \(y = \cos x\) là hàm số chẵn.
Tập xác định của hàm số \(y = 2\sin x\) là:
-
A.
\(\left[ { - 1;1} \right]\).
-
B.
\(\left( { - 1;1} \right)\).
-
C.
\(\mathbb{R}\).
-
D.
\(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Đáp án : C
Sử kiến thức về tập xác định của hàm số \(y = \sin x\): Hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\).
Hàm số \(y = 2\sin x\) có tập xác định là \(\mathbb{R}\).
Chọn khẳng định đúng:
-
A.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} - {u_n} < 0\) với mọi \(n \in \mathbb{N}*\).
-
B.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} - {u_n} > 0\) với mọi \(n \in \mathbb{N}*\).
-
C.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} + {u_n} < 0\) với mọi \(n \in \mathbb{N}*\).
-
D.
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} + {u_n} > 0\) với mọi \(n \in \mathbb{N}*\)
Đáp án : A
Sử dụng kiến thức về dãy số giảm: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} < {u_n}\) với mọi \(n \in \mathbb{N}*\)
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} < {u_n}\) với mọi \(n \in \mathbb{N}*\).
Tức là: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} - {u_n} < 0\) với mọi \(n \in \mathbb{N}*\).
Dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho 5. Số nào dưới đây thuộc dãy số \(\left( {{u_n}} \right)\)?
-
A.
1.
-
B.
3.
-
C.
5.
-
D.
7.
Đáp án : C
Sử dụng kiến thức về cách cho một dãy số bằng phương pháp mô tả.
Vì \(5 \vdots 5\) nên 5 thuộc dãy số \(\left( {{u_n}} \right)\).
Cấp số cộng nào dưới đây có công sai bằng 3?
-
A.
1; 3; 5; 7; 9; 11; ...
-
B.
1; 3; 9; 27; …
-
C.
11; 8; 5; 2; …
-
D.
0; 3; 6; 9; …
Đáp án : D
Sử dụng kiến thức về cấp số cộng: Cấp số cộng là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Xét dãy số: 0; 3; 6; 9; … ta thấy: Kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 3 nên dãy số 0; 3; 6; 9; … có công sai bằng 3.
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\). Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right)\)
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = 4\).
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = - 4\).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = 10\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = - 10\).
Đáp án : B
Sử dụng quy tắc về giới hạn dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) thì \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right) = a + b\).
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = 2 - 6 = - 4\)
Phát biểu nào sau đây là sai?
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = c\) (c là hằng số).
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\left( {\left| q \right| > 1} \right)\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^k}}} = 0\left( {k > 1} \right)\).
Đáp án : C
Sử dụng kiến thức giới hạn dãy số: \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\left( {\left| q \right| < 1} \right)\)
Vì \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\left( {\left| q \right| < 1} \right)\) nên C là câu sai.
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu:
-
A.
\(g\left( {{x_0}} \right) \ne 0\).
-
B.
\(f\left( {{x_0}} \right) \ne 0\).
-
C.
\(g\left( {{x_0}} \right) = 0\).
-
D.
\(f\left( {{x_0}} \right) = 0\).
Đáp án : A
Sử dụng kiến thức về tính chất cơ bản của hàm số liên tục: Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu \(g\left( {{x_0}} \right) \ne 0\).
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu \(g\left( {{x_0}} \right) \ne 0\).
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } {x^5}\) là:
-
A.
3.
-
B.
2.
-
C.
\( - 2\).
-
D.
\( + \infty \).
Đáp án : D
Sử dụng quy tắc tính giới hạn của hàm số: \(\mathop {\lim }\limits_{x \to + \infty } {x^k} = + \infty \) với k là số nguyên dương.
\(\mathop {\lim }\limits_{x \to + \infty } {x^5} = + \infty \)
Một mặt phẳng được xác định nếu mặt phẳng đó chứa:
-
A.
Ba điểm phân biệt.
-
B.
Một đường thẳng và một điểm thuộc đường thẳng đó.
-
C.
Hai đường thẳng cắt nhau.
-
D.
Hai đường thẳng phân biệt.
Đáp án : C
Sử dụng kiến thức về cách xác định một mặt phẳng: Một mặt phẳng hoàn toàn được xác định khi chứa hai đường thẳng cắt nhau.
Một mặt phẳng hoàn toàn được xác định khi chứa hai đường thẳng cắt nhau.
Cho hình chóp S. ABCD với ABCD là hình bình hành. Hai điểm S và B cùng thuộc hai mặt phẳng:
-
A.
(SAC) và (SBD).
-
B.
(SAB) và (SBD).
-
C.
(SAB) và (SDC).
-
D.
A, B, C đều sai.
Đáp án : B
Sử dụng kiến thức điểm thuộc mặt phẳng.
Hai điểm S và B cùng thuộc 2 mặt phẳng (SAB) và (SBD).
Trong các mệnh đề sau, mệnh đề nào đúng?
-
A.
Hai đường thẳng chéo nhau khi không có điểm chung.
-
B.
Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
-
C.
Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
-
D.
Hai đường thẳng song song khi và chỉ khi chúng ở trên cùng hai mặt phẳng.
Đáp án : C
Sử dụng kiến thức về vị trí hai đường thẳng song song.
Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
Cho hình hộp ABCD. A’B’C’D’. Hình hộp đó có bao nhiêu mặt bên?
-
A.
6.
-
B.
5.
-
C.
4.
-
D.
3.
Đáp án : C
Sử dụng kiến thức về hình hộp: Hình hộp ABCD. A’B’C’D’ có bốn mặt bên là ABB’A’, BCC’B’, CDD’C’, ADD’A’.
Hình hộp ABCD. A’B’C’D’ có bốn mặt bên là ABB’A’, BCC’B’, CDD’C’, ADD’A’.
Khẳng định nào sau đây là sai?
-
A.
Hình lăng trụ có hai mặt đáy bằng nhau.
-
B.
Hình lăng trụ có các mặt bên là hình bình hành.
-
C.
Hình lăng trụ có các cạnh bên bằng nhau.
-
D.
Hình lăng trụ có các mặt bên bằng nhau.
Đáp án : D
Sử dụng kiến thức về hình lăng trụ.
Trong hình lăng trụ, các mặt bên có thể không bằng nhau.
Ví dụ: Hình lăng trụ dưới đây có các mặt bên không bằng nhau
Qua phép chiếu song song, tính chất nào không được bảo toàn?
-
A.
Đồng quy.
-
B.
Song song.
-
C.
Chéo nhau.
-
D.
Thẳng hàng.
Đáp án : C
Sử dụng kiến thức về phép chiếu song song.
Qua phép chiếu song song, tính chất chéo nhau không được bảo toàn.
Biết rằng \(\tan \alpha = 2\). Giá trị biểu thức \(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }}\) \(\left( {\cos \alpha \ne 0} \right)\)là:
-
A.
\(\frac{4}{5}\).
-
B.
1.
-
C.
\(\frac{3}{5}\).
-
D.
\(\frac{5}{3}\).
Đáp án : A
Sử dụng công thức: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\).
\(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }} = \frac{{\frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{2\cos \alpha }}{{\cos \alpha }}}}{{\frac{{3\sin \alpha }}{{\cos \alpha }} - \frac{{\cos \alpha }}{{\cos \alpha }}}} = \frac{{\tan \alpha + 2}}{{3\tan \alpha - 1}} = \frac{{2 + 2}}{{3.2 - 1}} = \frac{4}{5}\)
Cho tam giác ABC. Chọn đáp án đúng:
-
A.
\(\sin \frac{{A + B}}{2} = \cos \frac{C}{2}\).
-
B.
\(\sin \frac{{A + B}}{2} = - \sin \frac{C}{2}\).
-
C.
\(\sin \frac{{A + B}}{2} = - \cos \frac{C}{2}\).
-
D.
\(\sin \frac{{A + B}}{2} = \sin \frac{C}{2}\).
Đáp án : A
Sử dụng công thức \(\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \)
Vì \(\widehat A + \widehat B + \widehat C = \pi \Rightarrow \frac{{\widehat A + \widehat B}}{2} = \frac{\pi }{2} - \frac{{\widehat C}}{2}\). Do đó: \(\sin \frac{{A + B}}{2} = \sin \left( {\frac{\pi }{2} - \frac{C}{2}} \right) = \cos \frac{C}{2}\)
Tập xác định của hàm số \(y = \frac{{2\sin x}}{{\sin x - \cos x}}\) là:
-
A.
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
-
B.
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
-
C.
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
-
D.
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Đáp án : C
Sử dụng kiến thức về tập xác định của hàm số: Hàm phân thức xác định khi mẫu thức khác 0.
Hàm số \(y = \frac{{2\sin x}}{{\sin x - \cos x}}\) xác định khi \(\sin x - \cos x \ne 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) \ne 0 \Leftrightarrow x \ne \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\)
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = \frac{{2n + 1}}{{n + 2}}\). Số \(\frac{{167}}{{84}}\) là số hạng thứ bao nhiêu của dãy số?
-
A.
240.
-
B.
250.
-
C.
260.
-
D.
270.
Đáp án : B
Thay \({u_n} = \frac{{167}}{{84}}\) vào số hạng tổng quát rồi tìm n.
Ta có: \(\frac{{167}}{{84}} = \frac{{2n + 1}}{{n + 2}} \Leftrightarrow 84\left( {2n + 1} \right) = 167\left( {n + 2} \right)\)
\(\Leftrightarrow 168n + 84 = 167n + 334 \Leftrightarrow n = 250\).
Do đó, số \(\frac{{167}}{{84}}\) là số hạng thứ 250 của dãy số.
Cho \(\left( {{u_n}} \right)\) là cấp số cộng thỏa mãn \({u_2} = 8;{u_4} = 12\). Số hạng đầu của cấp số cộng bằng:
-
A.
6.
-
B.
4.
-
C.
2.
-
D.
Đáp án khác.
Đáp án : A
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Theo đầu bài ta có hệ phương trình:
\(\left\{ \begin{array}{l}{u_2} = {u_1} + d\\{u_4} = {u_1} + 3d\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8 = {u_1} + d\\12 = {u_1} + 3d\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 6\\d = 2\end{array} \right.\)
Vậy số hạng đầu tiên của cấp số cộng là \({u_1} = 6\).
Tính tổng \(S = 1 + \frac{1}{2} + \frac{1}{4} + ... + \frac{1}{{{2^9}}}\)
-
A.
\(S = \frac{{1\;021}}{{511}}\).
-
B.
\(S = \frac{{1\;021}}{{512}}\).
-
C.
\(S = \frac{{1\;023}}{{511}}\).
-
D.
\(S = \frac{{1\;023}}{{512}}\).
Đáp án : D
Sử dụng kiến thức về công thức tổng của n số hạng đầu của cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q \ne 1\) thì \(S = {u_1} + {u_2} + ... + {u_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)
Cấp số nhân trên có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\). Do đó: \(S = \frac{{1.\left[ {1 - {{\left( {\frac{1}{2}} \right)}^{10}}} \right]}}{{1 - \frac{1}{2}}} = \frac{{1\;023}}{{512}}\)
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^4} - 2{x^2} - 1} \right)\) bằng:
-
A.
4.
-
B.
0.
-
C.
\( - \infty \).
-
D.
\( + \infty \).
Đáp án : D
Sử dụng kiến thức giới hạn hàm số: Nếu \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \), \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = L > 0\) thì \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right).g\left( x \right)} \right] = + \infty \).
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^4} - 2{x^2} - 1} \right) = \mathop {\lim }\limits_{x \to - \infty } {x^4}\left( {3 - \frac{2}{{{x^2}}} - \frac{1}{{{x^4}}}} \right)\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } {x^4} = + \infty \) và \(\mathop {\lim }\limits_{x \to - \infty } \left( {3 - \frac{2}{{{x^2}}} - \frac{1}{{{x^4}}}} \right) = 3 > 0\) nên \(\mathop {\lim }\limits_{x \to - \infty } {x^4}\left( {3 - \frac{2}{{{x^2}}} - \frac{1}{{{x^4}}}} \right) = + \infty \)
Chọn đáp án đúng:
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \frac{1}{4}\).
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = 3\).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \frac{1}{3}\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \frac{1}{2}\).
Đáp án : A
Sử dụng quy tắc về giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{1 - {{\left( {\frac{2}{3}} \right)}^n}}}{{4 + {{\left( {\frac{2}{3}} \right)}^n}}} = \frac{1}{4}\)
Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{{{x^3} - x}}\). Kết luận nào sau đây là đúng?
-
A.
Hàm số liên tục tại \(x = - 1\).
-
B.
Hàm số liên tục tại \(x = 0\).
-
C.
Hàm số liên tục tại \(x = 1\).
-
D.
Hàm số liên tục tại \(x = \frac{1}{4}\).
Đáp án : D
Sử dụng kiến thức về tính liên tục của hàm số sơ cấp cơ bản: Hàm phân thức hữu tỉ (thương là hai đa thức) liên tục trên tập xác định của chúng.
Hàm số f(x) xác định khi \({x^3} - x \ne 0 \Leftrightarrow x\left( {{x^2} - 1} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne \pm 1\end{array} \right.\)
Do đó, hàm số f(x) liên tục trên các khoảng \(\left( { - \infty ; - 1} \right),\left( { - 1;0} \right),\left( {0;1} \right),\left( {1; + \infty } \right)\)
Vậy hàm số liên tục tại \(x = \frac{1}{4}\)
Cho hình chóp tứ giác S. ABCD có BD và AC cắt nhau tại O. Trên SC lấy M không trùng với S và C, đường thẳng AM cắt SO tại K. Đường thẳng SD cắt đường thẳng nào?
-
A.
BC.
-
B.
BK.
-
C.
AC.
-
D.
AM.
Đáp án : B
Sử dụng kiến thức về hai đường thẳng cắt nhau.
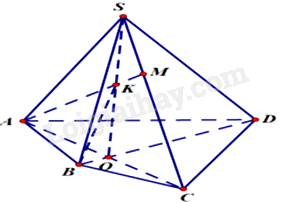
Vì hai đường thẳng SD và BK cùng nằm trong mặt phẳng (SBD) nên đường thẳng SD cắt đường thẳng BK.
Cho hình chóp S. ABCD có đáy là hình thang (AD// CB, \(BC < AD\)). Gọi M, N lần lượt là trung điểm của SA và SD. Khẳng định nào sau đây là đúng?
-
A.
MN//BC.
-
B.
MN\( \bot \)BC.
-
C.
MN cắt BC.
-
D.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng kiến thức về tính chất của hai đường thẳng song song: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
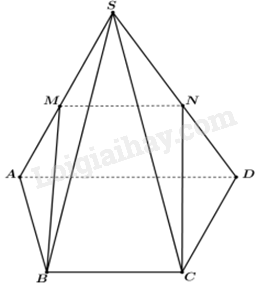
Vì M, N lần lượt là trung điểm của SA và SD nên MN là đường trung bình của tam giác SAD.
Do đó, MN//AD. Mà AD// CB nên MN//BC
Cho hình chóp S. ABCD có đáy ABCD là hình thang (AB//CD). Gọi O là giao điểm của AC và BD, I là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
-
A.
SI.
-
B.
SO.
-
C.
Đường thẳng qua S vuông góc với SI.
-
D.
Đường thẳng qua S song song với DC.
Đáp án : B
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là \(d = \left( P \right) \cap \left( Q \right)\).
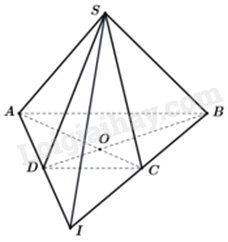
Ta có: S là điểm chung của hai mặt phẳng (SAC) và (SBD).
Vì O là giao điểm của AC và BD nên O là điểm chung của hai mặt phẳng (SAC) và (SBD).
Vậy giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, G lần lượt là các điểm thuộc SB, SC sao cho \(\frac{{SM}}{{MB}} = \frac{{SG}}{{GC}} = 2\). Tứ giác MGDA là hình gì?
-
A.
Hình thoi.
-
B.
Hình bình hành.
-
C.
Hình thang.
-
D.
Hình chữ nhật.
Đáp án : C
Sử dụng kiến thức về tính chất của hai đường thẳng song song: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
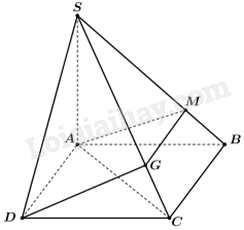
Tam giác SBC có: \(\frac{{SM}}{{MB}} = \frac{{SG}}{{GC}} = 2\) nên MG//BC (định lí Thalès đảo)
Mà BC// AD (Tứ giác ABCD là hình bình hành). Do đó, MG//AD. Suy ra, tứ giác MGDA là hình thang.
Tứ phân vị \({Q_2}\) của mẫu số liệu ghép nhóm là:
-
A.
Trung vị của mẫu số liệu ghép nhóm.
-
B.
Trung bình của mẫu số liệu ghép nhóm.
-
C.
Mốt của mẫu số liệu ghép nhóm.
-
D.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng kiến thức về tứ phân vị của mẫu số liệu ghép nhóm: Tứ phân vị \({Q_2}\) của mẫu số liệu ghép nhóm là trung vị của mẫu số liệu ghép nhóm.
Tứ phân vị \({Q_2}\) của mẫu số liệu ghép nhóm là trung vị của mẫu số liệu ghép nhóm.
Kết quả khảo sát cân nặng của 25 quả bơ ở một lô hàng cho trong bảng sau:

Nhóm \(\left[ {160;165} \right)\) có tần số là bao nhiêu?
-
A.
7.
-
B.
12.
-
C.
3.
-
D.
2.
Đáp án : B
Sử dụng kiến thức về tần số của mẫu số liệu ghép nhóm: Số giá trị của mẫu số liệu thuộc mỗi nhóm là tần số của nhóm đó.
Nhóm \(\left[ {160;165} \right)\) có tần số là 12.
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được cho ở trong bảng sau (đơn vị: Triệu đồng):

-
A.
7,7.
-
B.
8,7.
-
C.
7,5.
-
D.
8,5.
Đáp án : A
Sử dụng kiến thức số trung bình của mẫu số liệu ghép nhóm:
Cho mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu là: \(\frac{{4.3 + 6.6 + 8.4 + 10.5 + 12.2}}{{3 + 6 + 4 + 5 + 2}} = 7,7\)
Mẫu số liệu ghép nhóm dưới đây là thời gian (phút) từ nhà đến nơi làm việc của các nhân viên một công ty như sau:

Tứ phân vị thứ nhất của mẫu số liệu này là:
-
A.
\(\frac{{1360}}{{37}}\) phút.
-
B.
\(\frac{{136}}{5}\) phút.
-
C.
\(\frac{{1365}}{{37}}\) phút.
-
D.
\(\frac{{137}}{5}\) phút.
Đáp án : B
Sử dụng kiến thức về tìm tứ phân vị thứ nhất mẫu số liệu ghép nhóm:
Bước 1: Xác định nhóm chứa \({Q_1}\). Giả sử nhóm đó là nhóm thứ p: \(\left[ {{a_p};{a_{p + 1}}} \right)\)
Bước 2: Tứ phân vị thứ nhất là \({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}\left( {{a_{p + 1}} - {a_p}} \right)\)
Trong đó n là cỡ mẫu, \({m_p}\) là tần số của nhóm p. Với \(p = 1\), ta quy ước \({m_1} + ... + {m_{p - 1}} = 0\)
Cỡ mẫu: \(n = 128\)
Tứ phân vị thứ nhất là: \(\frac{{{x_{32}} + {x_{33}}}}{2}\). Do \({x_{32}},{x_{33}}\) đều thuộc nhóm \(\left[ {25;30} \right)\) nên nhóm này chứa \({Q_1}\).
Ta có: \(p = 3,{a_3} = 25;{m_3} = 25;{m_1} + {m_2} = 21,{a_4} - {a_3} = 5\)
Do đó, \({Q_1} = 25 + \frac{{\frac{{128}}{4} - 21}}{{25}}.5 = \frac{{136}}{5}\)
Sử dụng kiến thức về hàm số liên tục: Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này.
Tập xác định: \(D = \mathbb{R}\)
Khi \(x \in \left( { - \infty ;1} \right)\): Hàm số \(f\left( x \right) = mx + 3\) liên tục trên \(\left( { - \infty ;1} \right)\).
Khi \(x \in \left( {1; + \infty } \right)\): Hàm số \(f\left( x \right) = \frac{1}{{x - 1}} - \frac{3}{{{x^3} - 1}}\) liên tục trên \(\left( {1; + \infty } \right)\).
Tại \(x = 1\):
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\frac{1}{{x - 1}} - \frac{3}{{{x^3} - 1}}} \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} + x + 1 - 3}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} + x - 2}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\( = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 2}}{{{x^2} + x + 1}} = \frac{3}{3} = 1\)
\(\mathop {\lim }\limits_{x \to {1^ - }} \left( {mx + 3} \right) = m + 3\), \(f\left( 1 \right) = m + 3\)
Hàm số f(x) liên tục trên \(\mathbb{R}\) \( \Leftrightarrow \) hàm số f(x) liên tục tại \(x = 1\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right)\)
Tức là: \(m + 3 = 1 \Leftrightarrow m = - 2\)
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
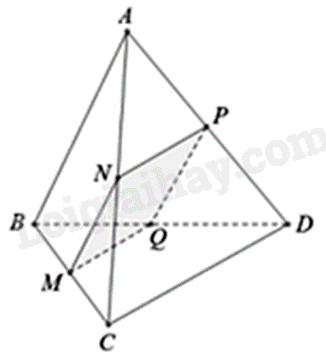
Vì (P) qua M và song song với AB nên \(\left( P \right) \cap \left( {ABC} \right) = MN\), với N là giao điểm của đường thẳng qua M song song với AB và cạnh AC.
Vì (P) qua N và song song với CD nên \(\left( P \right) \cap \left( {ACD} \right) = NP\), với P là giao điểm của đường thẳng qua N song song với CD và cạnh AD.
Vì (P) qua M và song song với CD nên \(\left( P \right) \cap \left( {BCD} \right) = MQ\), với Q là giao điểm của đường thẳng qua M song song với CD và cạnh BD.
Do đó, thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là tứ giác MNPQ.
Ta có: MN//PQ, \(MN = PQ = \frac{1}{2}AB\), MQ//PN, \(MQ = PN = \frac{1}{2}DC\), \(AB = CD\)
Do đó, \(MN = NP = PQ = QM\) nên tứ giác MNPQ là hình thoi.
Sử dụng kiến thức công thức: \({\cos ^2}x + {\sin ^2}x = 1\)
Ta có: \(y = 2{\cos ^2}x + 5\sin x + 1 = 2\left( {1 - {{\sin }^2}x} \right) + 5\sin x + 1 = - 2{\sin ^2}x + 5\sin x + 3\) (1)
Đặt \(\sin x = t\). Vì \(x \in \left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) nên \(t \in \left[ {\frac{1}{2};1} \right]\).
Thay \(\sin x = t\) vào (1) ta có: \(y = - 2{t^2} + 5t + 3\) với \(t \in \left[ {\frac{1}{2};1} \right]\)
Ta có bảng:
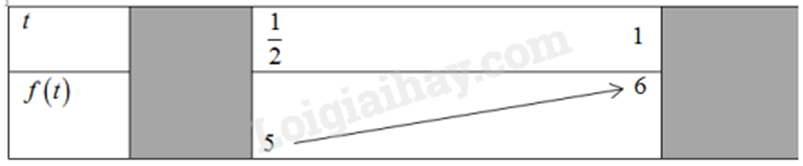
Từ bảng ta có:
Giá trị lớn nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) là 6 khi \(t = 1\) hay \(x = \frac{\pi }{2}\)
Giá trị nhỏ nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) là 5 khi \(t = \frac{1}{2}\) hay \(x = \frac{{5\pi }}{6}\)
Sử dụng kiến thức về công thức số hạng tổng quát của dãy số.
Ta có: \({u_{n + 1}} = \frac{1}{3}\left( {2{u_n} + \frac{{n - 1}}{{{n^2} + 3n + 2}}} \right) = \frac{1}{3}\left( {2{u_n} + \frac{3}{{n + 2}} - \frac{2}{{n + 1}}} \right) = \frac{2}{3}{u_n} + \frac{1}{{n + 2}} - \frac{2}{3}.\frac{1}{{n + 1}}\)
\( \Leftrightarrow {u_{n + 1}} - \frac{1}{{n + 2}} = \frac{2}{3}\left( {{u_n} - \frac{1}{{n + 1}}} \right)\) (1)
Đặt \({v_n} = {u_n} - \frac{1}{{n + 1}}\), từ (1) suy ra \({v_{n + 1}} = \frac{2}{3}{v_n}\)
Do đó, \(\left( {{v_n}} \right)\) là cấp số nhân với \({v_1} = {u_1} - \frac{1}{2} = \frac{1}{2}\), công bội \(q = \frac{2}{3}\)
Suy ra: \({v_n} = {v_1}.{q^{n - 1}} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{n - 1}} \Leftrightarrow {u_n} - \frac{1}{{n + 1}} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{n - 1}} \Leftrightarrow {u_n} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{n - 1}} + \frac{1}{{n + 1}}\)
Vậy \({u_{2020}} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{2019}} + \frac{1}{{2021}} = \frac{{{2^{2018}}}}{{{3^{2019}}}} + \frac{1}{{2021}}\)
Phần trắc nghiệm (7 điểm) Câu 1: Nghiệm của phương trình
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Đề thi học kì 1 Toán 11 - Đề số 9
Đề thi học kì 1 Toán 11 - Đề số 10
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (7 điểm) Câu 1: Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là
A. Nội dung ôn tập Hàm số lượng giác và phương trình lượng giác 1. Giá trị lượng giác của góc lượng giác 2. Công thức lượng giác 3. Hàm số lượng giác 4. Phương trình lượng giác cơ bản
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận