Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 2
Phần trắc nghiệm (7 điểm) Câu 1: Cho số thực dương a và số hữu tỉ $r=\frac{m}{n}$, trong đó $m,n\in \mathbb{Z},n>0$. Ta có:
Đề bài
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có:
-
A.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[{nm}]{a}\).
-
B.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[m]{{{a^n}}}\).
-
C.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
-
D.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{\sqrt[m]{a}}}\).
-
A.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\).
-
B.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{a}{{{b^\alpha }}}\).
-
C.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{b}\).
-
D.
Cả A, B, C đều sai.
Chọn đáp án đúng:
-
A.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[6]{5}\).
-
B.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[3]{{10}}\).
-
C.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt {{5^{^3}}} \).
-
D.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[3]{{{5^2}}}\).
Rút gọn biểu thức \({\left( {{a^{\sqrt 3 }}.{b^{\frac{{ - 6}}{{\sqrt 3 }}}}} \right)^{\frac{1}{{\sqrt 3 }}}}\) (với \(a,b > 0\)) được kết quả là:
-
A.
\({a^2}\).
-
B.
\(\frac{a}{{{b^2}}}\).
-
C.
\(\frac{b}{a}\).
-
D.
\(a{b^2}\).
Giá trị của biểu thức \({\left( {\sqrt 5 - 2} \right)^{2024}}.{\left( {\sqrt 5 + 2} \right)^{2025}}\)
-
A.
\(\sqrt 5 + 2\).
-
B.
\(\sqrt 5 - 2\).
-
C.
\( - \sqrt 5 + 2\).
-
D.
\( - \sqrt 5 - 2\).
-
A.
\({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\).
-
B.
\({\log _a}\left( {bc} \right) = {\log _a}b.{\log _a}c\).
-
C.
\({\log _a}\left( {bc} \right) = \frac{1}{2}{\log _a}b.{\log _a}c\).
-
D.
\({\log _a}\left( {bc} \right) = {\log _a}b - {\log _a}c\).
-
A.
\({\log _a}c = {\log _b}c.{\log _b}a\).
-
B.
\({\log _a}c = \frac{{{{\log }_b}c}}{{{{\log }_b}a}}\).
-
C.
\({\log _a}c = {\log _b}c + {\log _b}a\).
-
D.
\({\log _a}c = \frac{{{{\log }_a}c}}{{{{\log }_b}c}}\).
Khẳng định nào sau đây đúng?
-
A.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
-
B.
Lôgarit tự nhiên của số thực dương của a kí hiệu là \(\log a\).
-
C.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
-
D.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\ln a\).
Tính \({\log _8}1250\) theo a biết \(a = {\log _2}5\).
-
A.
\({\log _8}1250 = 4a + 3\).
-
B.
\({\log _8}1250 = \frac{4}{3}a + \frac{1}{3}\).
-
C.
\({\log _8}1250 = 2a + \frac{1}{3}\).
-
D.
\({\log _8}1250 = 2a - \frac{1}{3}\).
Chọn đáp án đúng:
-
A.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = \frac{5}{2}\).
-
B.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = 1\).
-
C.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = \frac{5}{4}\).
-
D.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = \frac{5}{3}\).
Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đi qua điểm:
-
A.
\(A\left( {1;0} \right)\).
-
B.
\(B\left( {0;1} \right)\).
-
C.
\(C\left( {0; - 1} \right)\).
-
D.
\(D\left( {a;0} \right)\).
Hàm số nào dưới đây là hàm số lôgarit cơ số 2?
-
A.
\(y = {2^x}\).
-
B.
\(y = {\log _x}2\).
-
C.
\(y = {\log _2}x\).
-
D.
\(y = \ln \left( {2x} \right)\).
Hàm số nào dưới đây nghịch biến trên \(\mathbb{R}\)?
-
A.
\(y = {2^x}\).
-
B.
\(y = {\left( {\frac{1}{2}} \right)^x}\).
-
C.
\(y = {e^x}\).
-
D.
\(y = {\pi ^x}\).
Tập giá trị của hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) là:
-
A.
\(T = \mathbb{R}\).
-
B.
\(T = \left( { - \infty ;0} \right)\).
-
C.
\(T = \left( {0; + \infty } \right)\).
-
D.
\(T = \left( { - 1;1} \right)\).
Tập xác định của hàm số \(y = {8^{\sqrt {{x^2} - 4} }}\) là:
-
A.
\(D = \left( { - 2;2} \right)\).
-
B.
\(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\).
-
C.
\(D = \left[ { - 2;2} \right]\).
-
D.
\(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right) = {\log _{\frac{1}{{\sqrt 3 }}}}x\). Biết rằng: \(\mathop {\max }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = M,\mathop {\min }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = m\). Khi đó:
-
A.
\(M.m = 2\).
-
B.
\(M.m = - 1\).
-
C.
\(M.m = 4\).
-
D.
\(M.m = 1\).
Với giá trị nào của b thì phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) vô nghiệm?
-
A.
\(b = {2^{ - 3}}\).
-
B.
\(b = 2\).
-
C.
\(b = 0\).
-
D.
\(b = \frac{1}{2}\).
Nghiệm của phương trình \({\left( {\sqrt 3 } \right)^x} = 3\) là:
-
A.
\(x = 0\).
-
B.
\(x = 2\).
-
C.
\(x = - 1\).
-
D.
\(x = 1\).
Phương trình \({\log _2}x = - 2\) có nghiệm là:
-
A.
\(x = - 4\).
-
B.
\(x = 4\).
-
C.
\(x = \frac{{ - 1}}{4}\).
-
D.
\(x = \frac{1}{4}\).
Nghiệm của phương trình \(0,{2^{x - 1}} = \frac{1}{{\sqrt {125} }}\) là:
-
A.
\(x = \frac{5}{2}\).
-
B.
\(x = \frac{5}{4}\).
-
C.
\(x = \frac{{ - 1}}{4}\).
-
D.
\(x = \frac{1}{2}\).
Tập nghiệm của phương trình \({\log _2}\left( {{{\log }_{16}}x} \right) = - 2\) là:
-
A.
\(S = \left\{ 3 \right\}\).
-
B.
\(S = \left\{ 2 \right\}\).
-
C.
\(S = \left\{ 4 \right\}\).
-
D.
\(S = \left\{ 5 \right\}\).
Bất phương trình \(2{\log _{\frac{1}{3}}}\left( {x + 1} \right) > {\log _{\frac{1}{3}}}\left( {3x + 7} \right)\) có nghiệm là:
-
A.
\( - 2 \le x \le 3\).
-
B.
\( - 2 < x < 3\).
-
C.
\( - 1 \le x < 3\).
-
D.
\( - 1 < x < 3\).
Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt 2 }}} \right)^{2x - 4}} \ge \frac{1}{4}\) là:
-
A.
\(S = \left[ {4; + \infty } \right)\).
-
B.
\(S = \left( {4; + \infty } \right)\).
-
C.
\(S = \left( { - \infty ;4} \right]\).
-
D.
\(S = \left( { - \infty ;4} \right)\).
Hai đường thẳng a, b được gọi là vuông góc với nhau nếu góc giữa chúng bằng:
-
A.
1800.
-
B.
1500.
-
C.
900.
-
D.
Cả A, B, C đều sai.
Trong không gian, khẳng định nào sau đây là đúng?
-
A.
Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng còn lại.
-
B.
Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì song song với đường thẳng còn lại.
-
C.
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
-
D.
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, \(SA = a\sqrt 3 \) và \(SA \bot BC\). Góc giữa SD và BC bằng:
-
A.
\({45^0}\).
-
B.
\({60^0}\).
-
C.
\({30^0}\).
-
D.
\({70^0}\).
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a. Gọi I, J lần lượt là trung điểm của SA và SC. Góc giữa IJ và BD bằng:
-
A.
\({60^0}\).
-
B.
\({90^0}\).
-
C.
\({80^0}\).
-
D.
\({70^0}\).
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (P) thì d vuông góc với bất kì đường thẳng nào nằm trong (P).
-
B.
Nếu đường thẳng d vuông góc với mặt phẳng (P) thì d vuông góc với hai đường thẳng nằm trong mặt phẳng (P).
-
C.
Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong mặt phẳng (P) thì d vuông góc với mặt phẳng (P).
-
D.
Nếu đường thẳng d vuông góc với mặt phẳng (P) thì nó vuông góc với bất kì đường thẳng nào trong mặt phẳng (P).
Tìm mệnh đề sai trong các mệnh đề sau:
-
A.
Cho hai đường thẳng chéo nhau và vuông góc nhau. Khi đó, có một và chỉ một mặt phẳng chứa hai đường thẳng này và vuông góc với đường thẳng kia.
-
B.
Qua một điểm O cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
-
C.
Qua một điểm O cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng cho trước.
-
D.
Qua một điểm O cho trước có duy nhất một đường thẳng vuông góc với một mặt phẳng cho trước.
Chọn đáp án đúng.
Trong không gian, cho đường thẳng d không nằm trong mặt phẳng (P), đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu d:
-
A.
Vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P).
-
B.
Vuông góc với đường thẳng a mà đường thẳng a song song mặt phẳng (P).
-
C.
Vuông góc với mọi đường thẳng nằm trong mặt phẳng (P).
-
D.
Vuông góc với đường thẳng a nằm trong mặt phẳng (P).
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b’ là hình chiếu vuông góc của b trên (P). Khi đó, a vuông góc với b khi và chỉ khi…
Cụm từ thích hợp điền vào… để được đáp án đúng là:
-
A.
a vuông góc với \(b'\).
-
B.
a song song với \(b'\).
-
C.
a cắt \(b'\).
-
D.
a và \(b'\) chéo nhau.
Cho hình chóp S. ABC có ABC là tam giác cân tại C, SA vuông góc với đáy. Gọi H, K lần lượt là trung điểm của AB và SB. Khẳng định nào dưới đây là sai?
-
A.
\(CH \bot AK\).
-
B.
\(CH \bot SB\).
-
C.
\(CH \bot SA\).
-
D.
\(SB \bot AK\).
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và tam giác ABC vuông tại B. Kẻ \(AH \bot SB\left( {H \in SB} \right)\). Khẳng định nào dưới đây là sai?
-
A.
\(BC \bot SA\).
-
B.
\(BC \bot AH\).
-
C.
\(AH \bot AC\).
-
D.
\(AH \bot SC\).
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O. Biết rằng \(SA = SC,SB = SD\). Khẳng định nào sau đây là đúng?
-
A.
\(AB \bot \left( {SAC} \right)\).
-
B.
\(CD \bot AC\).
-
C.
\(CD \bot \left( {SBD} \right)\).
-
D.
\(SO \bot \left( {ABCD} \right)\).
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Hình chiếu vuông góc của điểm D trên mặt phẳng (SAB) là điểm:
-
A.
S.
-
B.
A.
-
C.
B.
-
D.
E (với E là trung điểm của SB).
Lời giải và đáp án
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có:
-
A.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[{nm}]{a}\).
-
B.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[m]{{{a^n}}}\).
-
C.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
-
D.
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{\sqrt[m]{a}}}\).
Đáp án : C
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
-
A.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\).
-
B.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{a}{{{b^\alpha }}}\).
-
C.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{b}\).
-
D.
Cả A, B, C đều sai.
Đáp án : A
Cho a, b là những số thực dương, \(\alpha \) là số thực bất kì. Khi đó, \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\).
Cho a, b là những số thực dương, \(\alpha \) là số thực bất kì. Khi đó, \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\).
Đáp án A.
Chọn đáp án đúng:
-
A.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[6]{5}\).
-
B.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[3]{{10}}\).
-
C.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt {{5^{^3}}} \).
-
D.
\({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[3]{{{5^2}}}\).
Đáp án : D
\({\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\) (với các biểu thức đều có nghĩa).
Ta có: \({\left( {\sqrt[3]{5}} \right)^2} = \sqrt[3]{{{5^2}}}\).
Đáp án D.
Rút gọn biểu thức \({\left( {{a^{\sqrt 3 }}.{b^{\frac{{ - 6}}{{\sqrt 3 }}}}} \right)^{\frac{1}{{\sqrt 3 }}}}\) (với \(a,b > 0\)) được kết quả là:
-
A.
\({a^2}\).
-
B.
\(\frac{a}{{{b^2}}}\).
-
C.
\(\frac{b}{a}\).
-
D.
\(a{b^2}\).
Đáp án : B
\({\left( {{a^m}} \right)^n} = {a^{mn}},{a^{ - n}} = \frac{1}{{{a^n}}}\) (a khác 0).
\({\left( {{a^{\sqrt 3 }}.{b^{\frac{{ - 6}}{{\sqrt 3 }}}}} \right)^{\frac{1}{{\sqrt 3 }}}} = {\left( {{a^{\sqrt 3 }}} \right)^{\frac{1}{{\sqrt 3 }}}}.{\left( {{b^{\frac{{ - 6}}{{\sqrt 3 }}}}} \right)^{\frac{1}{{\sqrt 3 }}}} = a.{b^{\frac{{ - 6}}{3}}} = \frac{a}{{{b^2}}}\)
Đáp án B.
Giá trị của biểu thức \({\left( {\sqrt 5 - 2} \right)^{2024}}.{\left( {\sqrt 5 + 2} \right)^{2025}}\)
-
A.
\(\sqrt 5 + 2\).
-
B.
\(\sqrt 5 - 2\).
-
C.
\( - \sqrt 5 + 2\).
-
D.
\( - \sqrt 5 - 2\).
Đáp án : A
\({\left( {{a^m}} \right)^n} = {a^{mn}},{a^m}.{b^m} = {\left( {a.b} \right)^m},{a^m}.{a^n} = {a^{m + n}}\) (a khác 0).
\({\left( {\sqrt 5 - 2} \right)^{2024}}.{\left( {\sqrt 5 + 2} \right)^{2025}} = {\left( {\sqrt 5 - 2} \right)^{2024}}.{\left( {\sqrt 5 + 2} \right)^{2024}}.\left( {\sqrt 5 + 2} \right)\)
\( = {\left[ {\left( {\sqrt 5 - 2} \right)\left( {\sqrt 5 + 2} \right)} \right]^{2024}}.\left( {\sqrt 5 + 2} \right) = {\left( {5 - 4} \right)^{2024}}\left( {\sqrt 5 + 2} \right) = \sqrt 5 + 2\)
Đáp án A.
-
A.
\({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\).
-
B.
\({\log _a}\left( {bc} \right) = {\log _a}b.{\log _a}c\).
-
C.
\({\log _a}\left( {bc} \right) = \frac{1}{2}{\log _a}b.{\log _a}c\).
-
D.
\({\log _a}\left( {bc} \right) = {\log _a}b - {\log _a}c\).
Đáp án : A
Với \(0 < a \ne 1,b,c > 0\) thì \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\).
Với \(0 < a \ne 1,b,c > 0\) thì \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\).
Đáp án A.
-
A.
\({\log _a}c = {\log _b}c.{\log _b}a\).
-
B.
\({\log _a}c = \frac{{{{\log }_b}c}}{{{{\log }_b}a}}\).
-
C.
\({\log _a}c = {\log _b}c + {\log _b}a\).
-
D.
\({\log _a}c = \frac{{{{\log }_a}c}}{{{{\log }_b}c}}\).
Đáp án : B
Với a, b, c là các số dương và \(a \ne 1,b \ne 1\) thì \({\log _a}c = \frac{{{{\log }_b}c}}{{{{\log }_b}a}}\).
Với a, b, c là các số dương và \(a \ne 1,b \ne 1\) thì \({\log _a}c = \frac{{{{\log }_b}c}}{{{{\log }_b}a}}\).
Đáp án B.
Khẳng định nào sau đây đúng?
-
A.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
-
B.
Lôgarit tự nhiên của số thực dương của a kí hiệu là \(\log a\).
-
C.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
-
D.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\ln a\).
Đáp án : D
Lôgarit cơ số e của số thực dương b được gọi là lôgarit tự nhiên của b và kí hiệu ln b.
Lôgarit tự nhiên của số thực dương a kí hiệu là \(\ln a\).
Đáp án D.
Tính \({\log _8}1250\) theo a biết \(a = {\log _2}5\).
-
A.
\({\log _8}1250 = 4a + 3\).
-
B.
\({\log _8}1250 = \frac{4}{3}a + \frac{1}{3}\).
-
C.
\({\log _8}1250 = 2a + \frac{1}{3}\).
-
D.
\({\log _8}1250 = 2a - \frac{1}{3}\).
Đáp án : B
Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{b^\alpha } = \alpha {\log _a}b,\log {\,_a}a = 1\), \({\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b\)
Với a là số thực dương, \(a \ne 1\), \(M > 0,N > 0\) thì \({\log _a}MN = {\log _a}M + {\log _a}N\).
\({\log _8}1250 = {\log _{{2^3}}}\left( {{5^4}.2} \right) = \frac{1}{3}\left( {{{\log }_2}{5^4} + {{\log }_2}2} \right) = \frac{4}{3}{\log _2}5 + \frac{1}{3} = \frac{4}{3}a + \frac{1}{3}\)
Đáp án B.
Chọn đáp án đúng:
-
A.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = \frac{5}{2}\).
-
B.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = 1\).
-
C.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = \frac{5}{4}\).
-
D.
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = \frac{5}{3}\).
Đáp án : A
Với a, b là số thực dương và \(a \ne 1\) thì \(\log {\,_a}a = 1;{\log _a}{b^\alpha } = \alpha {\log _a}b,{\log _a}{a^\alpha } = \alpha \).
\({\log _a}\left( {{a^2}\sqrt[3]{{a\sqrt a }}} \right) = {\log _a}\left( {{a^2}{{\left( {a.{a^{\frac{1}{2}}}} \right)}^{\frac{1}{3}}}} \right) = {\log _a}\left( {{a^2}.{a^{\frac{1}{2}}}} \right) = {\log _a}{a^{\frac{5}{2}}} = \frac{5}{2}\)
Đáp án A.
Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đi qua điểm:
-
A.
\(A\left( {1;0} \right)\).
-
B.
\(B\left( {0;1} \right)\).
-
C.
\(C\left( {0; - 1} \right)\).
-
D.
\(D\left( {a;0} \right)\).
Đáp án : A
Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đi qua điểm \(\left( {1;0} \right)\) và điểm \(\left( {a;1} \right)\).
Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đi qua điểm \(\left( {1;0} \right)\).
Đáp án A.
Hàm số nào dưới đây là hàm số lôgarit cơ số 2?
-
A.
\(y = {2^x}\).
-
B.
\(y = {\log _x}2\).
-
C.
\(y = {\log _2}x\).
-
D.
\(y = \ln \left( {2x} \right)\).
Đáp án : C
Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số lôgarit cơ số a.
Hàm số \(y = {\log _2}x\) có cơ số là 2.
Đáp án C.
Hàm số nào dưới đây nghịch biến trên \(\mathbb{R}\)?
-
A.
\(y = {2^x}\).
-
B.
\(y = {\left( {\frac{1}{2}} \right)^x}\).
-
C.
\(y = {e^x}\).
-
D.
\(y = {\pi ^x}\).
Đáp án : B
Nếu \(0 < a < 1\) thì hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) nghịch biến trên \(\mathbb{R}\).
Vì \(0 < \frac{1}{2} < 1\) nên hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên \(\mathbb{R}\).
Đáp án B.
Tập giá trị của hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) là:
-
A.
\(T = \mathbb{R}\).
-
B.
\(T = \left( { - \infty ;0} \right)\).
-
C.
\(T = \left( {0; + \infty } \right)\).
-
D.
\(T = \left( { - 1;1} \right)\).
Đáp án : C
Tập giá trị của hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) là \(T = \left( {0; + \infty } \right)\).
Tập giá trị của hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) là \(T = \left( {0; + \infty } \right)\).
Đáp án C.
Tập xác định của hàm số \(y = {8^{\sqrt {{x^2} - 4} }}\) là:
-
A.
\(D = \left( { - 2;2} \right)\).
-
B.
\(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\).
-
C.
\(D = \left[ { - 2;2} \right]\).
-
D.
\(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Đáp án : B
Hàm số \(y = \sqrt {u\left( x \right)} \) xác định khi \(u\left( x \right) \ge 0\).
Hàm số \(y = {8^{\sqrt {{x^2} - 4} }}\) xác định khi \({x^2} - 4 \ge 0 \Leftrightarrow \left( {x - 2} \right)\left( {x + 2} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - 2\end{array} \right.\)
Vậy tập xác định của hàm số \(y = {8^{\sqrt {{x^2} - 4} }}\) là: \(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\)
Đáp án B.
Cho hàm số \(y = f\left( x \right) = {\log _{\frac{1}{{\sqrt 3 }}}}x\). Biết rằng: \(\mathop {\max }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = M,\mathop {\min }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = m\). Khi đó:
-
A.
\(M.m = 2\).
-
B.
\(M.m = - 1\).
-
C.
\(M.m = 4\).
-
D.
\(M.m = 1\).
Đáp án : B
Cho hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\):
+ Nếu \(a > 1\) thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\).
+ Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {\log _{\frac{1}{{\sqrt 3 }}}}x\) có \(0 < \frac{1}{{\sqrt 3 }} < 1\) nên nghịch biến trên \(\left( {0; + \infty } \right)\).
Do đó, \(\mathop {\max }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = f\left( {\frac{1}{3}} \right) = {\log _{\frac{1}{{\sqrt 3 }}}}\frac{1}{3} = 2,\mathop {\min }\limits_{x \in \left[ {\frac{1}{3};3} \right]} y = f\left( 3 \right) = {\log _{\frac{1}{{\sqrt 3 }}}}3 = - 2\)
Do đó, \(M.m = - 1\)
Đáp án B.
Với giá trị nào của b thì phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) vô nghiệm?
-
A.
\(b = {2^{ - 3}}\).
-
B.
\(b = 2\).
-
C.
\(b = 0\).
-
D.
\(b = \frac{1}{2}\).
Đáp án : C
Cho phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\): Nếu \(b \le 0\) thì phương trình vô nghiệm.
Phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) vô nghiệm khi \(b \le 0\).
Do đó, \(b = 0\) thì phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) vô nghiệm.
Đáp án C.
Nghiệm của phương trình \({\left( {\sqrt 3 } \right)^x} = 3\) là:
-
A.
\(x = 0\).
-
B.
\(x = 2\).
-
C.
\(x = - 1\).
-
D.
\(x = 1\).
Đáp án : B
\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
\({\left( {\sqrt 3 } \right)^x} = 3 \Leftrightarrow {\left( {\sqrt 3 } \right)^x} = {\left( {\sqrt 3 } \right)^2} \Leftrightarrow x = 2\)
Vậy phương trình đã cho có nghiệm \(x = 2\)
Đáp án B.
Phương trình \({\log _2}x = - 2\) có nghiệm là:
-
A.
\(x = - 4\).
-
B.
\(x = 4\).
-
C.
\(x = \frac{{ - 1}}{4}\).
-
D.
\(x = \frac{1}{4}\).
Đáp án : D
Phương trình \({\log _a}x = b\left( {a > 0,a \ne 1} \right)\) luôn có nghiệm duy nhất \(x = {a^b}\).
Điều kiện: \(x > 0\)
\({\log _2}x = - 2 \Leftrightarrow x = {2^{ - 2}} = \frac{1}{4}\) (thỏa mãn)
Vậy phương trình có nghiệm \(x = \frac{1}{4}\).
Đáp án D.
Nghiệm của phương trình \(0,{2^{x - 1}} = \frac{1}{{\sqrt {125} }}\) là:
-
A.
\(x = \frac{5}{2}\).
-
B.
\(x = \frac{5}{4}\).
-
C.
\(x = \frac{{ - 1}}{4}\).
-
D.
\(x = \frac{1}{2}\).
Đáp án : A
\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
\(0,{2^{x - 1}} = \frac{1}{{\sqrt {125} }} \Leftrightarrow {\left( {\frac{1}{{\sqrt 5 }}} \right)^{2\left( {x - 1} \right)}} = {\left( {\frac{1}{{\sqrt 5 }}} \right)^3} \Leftrightarrow 2x - 2 = 3 \Leftrightarrow x = \frac{5}{2}\)
Đáp án A.
Tập nghiệm của phương trình \({\log _2}\left( {{{\log }_{16}}x} \right) = - 2\) là:
-
A.
\(S = \left\{ 3 \right\}\).
-
B.
\(S = \left\{ 2 \right\}\).
-
C.
\(S = \left\{ 4 \right\}\).
-
D.
\(S = \left\{ 5 \right\}\).
Đáp án : B
Với \(a > 0,a \ne 1\) ta có: \({\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}\).
Điều kiện: \(x > 0\)
\({\log _2}\left( {{{\log }_{16}}x} \right) = - 2 \Leftrightarrow {\log _{16}}x = {2^{ - 2}} = \frac{1}{4} \Leftrightarrow x = {16^{\frac{1}{4}}} = 2\)
Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left\{ 2 \right\}\).
Đáp án B.
Bất phương trình \(2{\log _{\frac{1}{3}}}\left( {x + 1} \right) > {\log _{\frac{1}{3}}}\left( {3x + 7} \right)\) có nghiệm là:
-
A.
\( - 2 \le x \le 3\).
-
B.
\( - 2 < x < 3\).
-
C.
\( - 1 \le x < 3\).
-
D.
\( - 1 < x < 3\).
Đáp án : D
Nếu \(0 < a < 1\) thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\)).
Điều kiện: \(x > - 1\)
\(2{\log _{\frac{1}{3}}}\left( {x + 1} \right) > {\log _{\frac{1}{3}}}\left( {3x + 7} \right) \Leftrightarrow {\log _{\frac{1}{3}}}{\left( {x + 1} \right)^2} > {\log _{\frac{1}{3}}}\left( {3x + 7} \right) \Leftrightarrow {\left( {x + 1} \right)^2} < 3x + 7 \Leftrightarrow {x^2} - x - 6 < 0\)
\( \Leftrightarrow \left( {x - 3} \right)\left( {x + 2} \right) < 0 \Leftrightarrow - 2 < x < 3\)
Kết hợp với điều kiện ta có: \( - 1 < x < 3\).
Đáp án D.
Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt 2 }}} \right)^{2x - 4}} \ge \frac{1}{4}\) là:
-
A.
\(S = \left[ {4; + \infty } \right)\).
-
B.
\(S = \left( {4; + \infty } \right)\).
-
C.
\(S = \left( { - \infty ;4} \right]\).
-
D.
\(S = \left( { - \infty ;4} \right)\).
Đáp án : C
Với \(a > 1\) thì \({a^{u\left( x \right)}} \ge {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) \ge v\left( x \right)\).
\({\left( {\frac{1}{{\sqrt 2 }}} \right)^{2x - 4}} \ge \frac{1}{4} \Leftrightarrow {2^{\frac{{2x - 4}}{{ - 2}}}} \ge {2^{ - 2}} \Leftrightarrow - x + 2 \ge - 2 \Leftrightarrow x \le 4\)
Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left( { - \infty ;4} \right]\).
Đáp án C.
Hai đường thẳng a, b được gọi là vuông góc với nhau nếu góc giữa chúng bằng:
-
A.
1800.
-
B.
1500.
-
C.
900.
-
D.
Cả A, B, C đều sai.
Đáp án : C
Hai đường thẳng a, b được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
Hai đường thẳng a, b được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
Đáp án C.
Trong không gian, khẳng định nào sau đây là đúng?
-
A.
Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng còn lại.
-
B.
Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì song song với đường thẳng còn lại.
-
C.
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
-
D.
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Đáp án : A
Trong không gian, cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng còn lại.
Trong không gian, cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng còn lại.
Đáp án A.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, \(SA = a\sqrt 3 \) và \(SA \bot BC\). Góc giữa SD và BC bằng:
-
A.
\({45^0}\).
-
B.
\({60^0}\).
-
C.
\({30^0}\).
-
D.
\({70^0}\).
Đáp án : B
+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).
+ Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
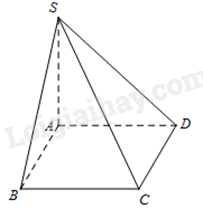
Vì ABCD là hình thoi nên BC//AD. Do đó, \(\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA}\)
Vì BC//AD, \(SA \bot BC\) nên \(SA \bot AD\). Do đó, tam giác SAD vuông tại A, suy ra:
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^0}\)
Đáp án B.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a. Gọi I, J lần lượt là trung điểm của SA và SC. Góc giữa IJ và BD bằng:
-
A.
\({60^0}\).
-
B.
\({90^0}\).
-
C.
\({80^0}\).
-
D.
\({70^0}\).
Đáp án : B
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
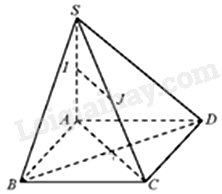
Vì I, J lần lượt là trung điểm của các cạnh SA và SC nên IJ là đường trung bình của tam giác SAC, do đó, IJ//AC.
Vì ABCD là hình thoi nên \(AC \bot BD\)
Vì \(AC \bot BD\), IJ//AC nên \(BD \bot IJ \Rightarrow \left( {BD,IJ} \right) = {90^0}\).
Đáp án B.
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (P) thì d vuông góc với bất kì đường thẳng nào nằm trong (P).
-
B.
Nếu đường thẳng d vuông góc với mặt phẳng (P) thì d vuông góc với hai đường thẳng nằm trong mặt phẳng (P).
-
C.
Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong mặt phẳng (P) thì d vuông góc với mặt phẳng (P).
-
D.
Nếu đường thẳng d vuông góc với mặt phẳng (P) thì nó vuông góc với bất kì đường thẳng nào trong mặt phẳng (P).
Đáp án : B
Nếu đường thẳng d vuông góc với hai đường thẳng phân biệt nằm trong mặt phẳng (P) thì d vuông góc với mặt phẳng (P).
Câu sai vì d phải vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (P) thì d vuông góc với (P).
Các đáp án còn lại đều đúng.
Đáp án B.
Tìm mệnh đề sai trong các mệnh đề sau:
-
A.
Cho hai đường thẳng chéo nhau và vuông góc nhau. Khi đó, có một và chỉ một mặt phẳng chứa hai đường thẳng này và vuông góc với đường thẳng kia.
-
B.
Qua một điểm O cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
-
C.
Qua một điểm O cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng cho trước.
-
D.
Qua một điểm O cho trước có duy nhất một đường thẳng vuông góc với một mặt phẳng cho trước.
Đáp án : B
Qua một điểm O cho trước có vô số đường thẳng vuông góc với đường thẳng cho trước cho trước.
Qua một điểm O cho trước có vô số đường thẳng vuông góc với đường thẳng cho trước cho trước nên đáp án B sai.
Hình minh họa:
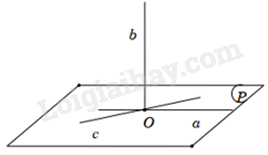
Các đáp án còn lại đều đúng.
Đáp án B.
Chọn đáp án đúng.
Trong không gian, cho đường thẳng d không nằm trong mặt phẳng (P), đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu d:
-
A.
Vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P).
-
B.
Vuông góc với đường thẳng a mà đường thẳng a song song mặt phẳng (P).
-
C.
Vuông góc với mọi đường thẳng nằm trong mặt phẳng (P).
-
D.
Vuông góc với đường thẳng a nằm trong mặt phẳng (P).
Đáp án : C
Trong không gian, cho đường thẳng d không nằm trong mặt phẳng (P), đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu d vuông góc với mọi đường thẳng nằm trong mặt phẳng (P).
Trong không gian, cho đường thẳng d không nằm trong mặt phẳng (P), đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu d vuông góc với mọi đường thẳng nằm trong mặt phẳng (P).
Đáp án C.
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b’ là hình chiếu vuông góc của b trên (P). Khi đó, a vuông góc với b khi và chỉ khi…
Cụm từ thích hợp điền vào… để được đáp án đúng là:
-
A.
a vuông góc với \(b'\).
-
B.
a song song với \(b'\).
-
C.
a cắt \(b'\).
-
D.
a và \(b'\) chéo nhau.
Đáp án : A
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b’ là hình chiếu vuông góc của b trên (P). Khi đó, a vuông góc với b khi và chỉ khi a vuông góc với \(b'\).
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b’ là hình chiếu vuông góc của b trên (P). Khi đó, a vuông góc với b khi và chỉ khi a vuông góc với \(b'\).
Đáp án A.
Cho hình chóp S. ABC có ABC là tam giác cân tại C, SA vuông góc với đáy. Gọi H, K lần lượt là trung điểm của AB và SB. Khẳng định nào dưới đây là sai?
-
A.
\(CH \bot AK\).
-
B.
\(CH \bot SB\).
-
C.
\(CH \bot SA\).
-
D.
\(SB \bot AK\).
Đáp án : D
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
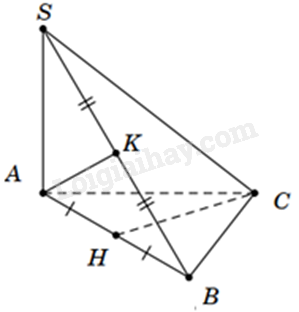
Vì H là trung điểm của AB, mà tam giác ABC cân tại C nên \(CH \bot AB\).
Ta có: \(SA \bot \left( {ABC} \right),CH \subset \left( {ABC} \right) \Rightarrow SA \bot CH\)
Ta có: \(CH \bot AB\), \(SA \bot CH\), SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên \(CH \bot \left( {SAB} \right)\). Mà \(AK,SB \subset \left( {SAB} \right) \Rightarrow AK \bot CH,SB \bot CH\)
Do đó, đáp án sai là D.
Đáp án D.
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và tam giác ABC vuông tại B. Kẻ \(AH \bot SB\left( {H \in SB} \right)\). Khẳng định nào dưới đây là sai?
-
A.
\(BC \bot SA\).
-
B.
\(BC \bot AH\).
-
C.
\(AH \bot AC\).
-
D.
\(AH \bot SC\).
Đáp án : C
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
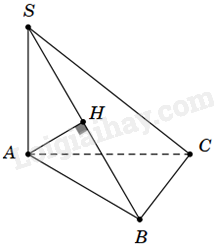
Vì \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\).
Tam giác ABC vuông tại B nên \(AB \bot BC\)
Ta có: \(SA \bot BC\), \(AB \bot BC\), SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên \(BC \bot \left( {SAB} \right)\). Mà \(AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH\)
Ta có: \(BC \bot AH,AH \bot SB\), SB và BC cắt nhau tại B và nằm trong mặt phẳng (SBC). Do đó, \(AH \bot \left( {SBC} \right)\), mà \(SC \subset \left( {SBC} \right) \Rightarrow SC \bot AH\)
Nếu \(AH \bot AC\), mà \(SA \bot AC \Rightarrow AC \bot \left( {SAH} \right) \Rightarrow AB \bot AC\) (vô lí)
Đáp án C.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O. Biết rằng \(SA = SC,SB = SD\). Khẳng định nào sau đây là đúng?
-
A.
\(AB \bot \left( {SAC} \right)\).
-
B.
\(CD \bot AC\).
-
C.
\(CD \bot \left( {SBD} \right)\).
-
D.
\(SO \bot \left( {ABCD} \right)\).
Đáp án : D
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
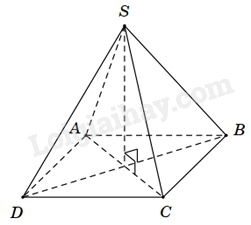
Vì \(SA = SC\) nên tam giác SAC cân tại S, mà SO là đường trung tuyến nên SO là đường cao của tam giác SAC. Do đó, \(SO \bot AC\) (1)
Vì \(SB = SD\) nên tam giác SBD cân tại S, mà SO là đường trung tuyến nên SO là đường cao của tam giác SBD. Do đó, \(SO \bot BD\) (2)
Lại có: BD và AC cắt nhau tại O và nằm trong mặt phẳng (ABCD) (3).
Từ (1), (2) và (3) ta có: \(SO \bot \left( {ABCD} \right)\).
Đáp án D.
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Hình chiếu vuông góc của điểm D trên mặt phẳng (SAB) là điểm:
-
A.
S.
-
B.
A.
-
C.
B.
-
D.
E (với E là trung điểm của SB).
Đáp án : B
Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
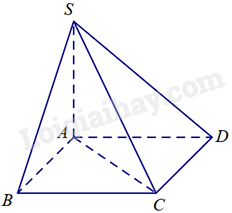
Vì \(SA \bot \left( {ABCD} \right),AD \subset \left( {ABCD} \right) \Rightarrow SA \bot AD\)
Vì ABCD là hình chữ nhật nên \(AB \bot AD\).
Mà SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB). Do đó, \(AD \bot \left( {SAB} \right)\).
Do đó, A là hình chiếu vuông góc của điểm D trên mặt phẳng (SAB).
Đáp án B.
Hàm số \(y = \ln u\left( x \right)\) xác định khi \(u\left( x \right) > 0\).
a) Với \(m = 1\) ta có: \(y = \ln \left( {{x^2} - 2x + 1} \right)\).
Hàm số \(y = \ln \left( {{x^2} - 2x + 1} \right)\) xác định khi \({x^2} - 2x + 1 > 0 \Leftrightarrow {\left( {x - 1} \right)^2} > 0 \Leftrightarrow x - 1 \ne 0 \Leftrightarrow x \ne 1\).
Vậy với \(m = 1\) thì tập xác định của hàm số là: \(D = \left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\).
b) Hàm số \(y = \ln \left[ {\left( {2 - m} \right){x^2} - 2x + 1} \right]\) xác định với mọi giá trị thực của x khi và chỉ khi \(f\left( x \right) = \left( {2 - m} \right){x^2} - 2x + 1 > 0\) với mọi \(x \in \mathbb{R}\)
Trường hợp 1: Với \(m = 2\) ta có: \(f\left( x \right) = - 2x + 1 > 0 \Leftrightarrow x < \frac{1}{2}\). Do đó, f(x) không xác định với mọi giá trị thực của x. Do đó, \(m = 2\) không thỏa mãn
Trường hợp 2: Với \(m \ne 2\). Hàm số \(f\left( x \right) = \left( {2 - m} \right){x^2} - 2x + 1 > 0\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}2 - m > 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 2\\{\left( { - 1} \right)^2} - \left( {2 - m} \right).1 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 2\\m > 1\end{array} \right. \Leftrightarrow 1 < m < 2\)
Vậy với \(1 < m < 2\) thì hàm số \(y = \ln \left[ {\left( {2 - m} \right){x^2} - 2x + 1} \right]\) có tập xác định với mọi giá trị thực của x.
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
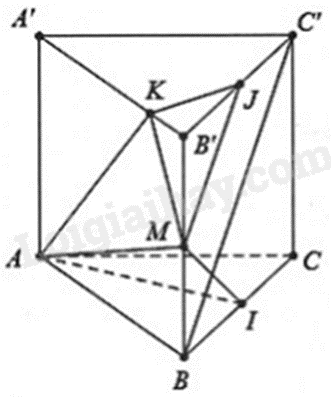
a) Vì tam giác ABC là tam giác đều và I là trung điểm của BC nên \(AI \bot BC\).
Mặt khác, \(AI \bot CC'\) (do \(CC' \bot \left( {ABC} \right)\)) và BC và CC’ cắt nhau tại C và nằm trong mặt phẳng (BCC’B’) nên \(AI \bot \left( {BCC'B'} \right) \Rightarrow AI \bot BC'\) (1)
Dễ dàng chứng minh được tứ giác BCC’B’ là hình vuông nên \(BC' \bot B'C\).
Vì M, I lần lượt là trung điểm của BB’, BC nên MI là đường trung bình của tam giác BB’C. Do đó, MI//B’C. Mà \(BC' \bot B'C\) nên \(MI \bot BC'\) (2)
Lại có: \(AI \bot BC'\) và MI và AI cắt nhau tại I và nằm trong mặt phẳng (AIM) (3)
Từ (1), (2) và (3) suy ra \(BC' \bot \left( {AIM} \right) \Rightarrow BC' \bot AM\).
b) Tam giác KMB’ vuông tại B’ nên \(\tan \widehat {KMB'} = \frac{{KB'}}{{MB'}} = \frac{1}{2}\).
Tam giác AMB vuông tại B nên \(\tan \widehat {AMB} = \frac{{AB}}{{BM}} = 2\).
Do đó, \(\tan \widehat {KMB'} = \cot \widehat {AMB} \Rightarrow \widehat {KMB'} + \widehat {AMB} = {90^o}\).
Suy ra, \(\widehat {AMK} = {90^o} \Rightarrow AM \bot MK\).
Ta có MJ là đường trung bình của tam giác B’BC’ nên MJ // BC’.
Mà \(BC' \bot \left( {AIM} \right)\) (cmt). Do đó \(MJ \bot \left( {AIM} \right) \Rightarrow MJ \bot AM\).
Mà \(AM \bot MK\). Do đó, \(AM \bot \left( {MKJ} \right) \Rightarrow AM \bot KJ\).
Nếu \(a > 0,a \ne 1\) thì \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\))
Điều kiện:
\({\log _2}\left( {{4^x} + 4} \right) = x - {\log _{0,5}}\left( {{2^{x + 1}} - 3} \right) \Leftrightarrow {\log _2}\left( {{4^x} + 4} \right) = x + {\log _2}\left( {{2^{x + 1}} - 3} \right) \Leftrightarrow x = {\log _2}\frac{{{{\left( {{2^x}} \right)}^2} + 4}}{{{{2.2}^x} - 3}}\)
\( \Leftrightarrow \frac{{{{\left( {{2^x}} \right)}^2} + 4}}{{{{2.2}^x} - 3}} = {2^x} \Rightarrow {2^x}\left( {{{2.2}^x} - 3} \right) = {\left( {{2^x}} \right)^2} + 4 \Rightarrow {\left( {{2^x}} \right)^2} - {3.2^x} - 4 = 0\) (*)
Đặt \({2^x} = t\left( {t > 0} \right)\) thì phương trình (*) trở thành: \({t^2} - 3t - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1\left( L \right)\\t = 4\left( {TM} \right)\end{array} \right.\)
Với \(t = 4\) thì \({2^x} = 4 \Leftrightarrow x = 2\) (thỏa mãn điều kiện)
Vậy phương trình có nghiệm là: \(x = 2\).
Phần trắc nghiệm (7 điểm) Câu 1: Cho $a>0,m,n\in \mathbb{R}$. Khẳng định nào sau đây là đúng?
Phần trắc nghiệm (7 điểm) Câu 1: Khẳng định nào sau đây là đúng?
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng. Với a là số thực khác 0 thì:
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Đề thi giữa kì 2 Toán 11 - Đề số 9
Đề thi giữa kì 2 Toán 11 - Đề số 10
Phần trắc nghiệm (7 điểm) Câu 1: Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận