Đề bài
Tìm mệnh đề sai trong các mệnh đề sau:
-
A.
Cho hai đường thẳng chéo nhau và vuông góc nhau. Khi đó, có một và chỉ một mặt phẳng chứa hai đường thẳng này và vuông góc với đường thẳng kia.
-
B.
Qua một điểm O cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
-
C.
Qua một điểm O cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng cho trước.
-
D.
Qua một điểm O cho trước có duy nhất một đường thẳng vuông góc với một mặt phẳng cho trước.
Phương pháp giải
Qua một điểm O cho trước có vô số đường thẳng vuông góc với đường thẳng cho trước cho trước.
Lời giải của GV Loigiaihay.com
Qua một điểm O cho trước có vô số đường thẳng vuông góc với đường thẳng cho trước cho trước nên đáp án B sai.
Hình minh họa:
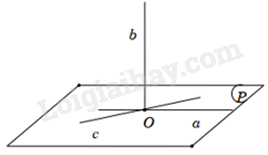
Các đáp án còn lại đều đúng.
Đáp án B.
Đáp án : B








Danh sách bình luận