Đề thi học kì 1 Toán 11 - Đề số 9
Đề thi học kì 1 Toán 11 - Đề số 9
Đề bài
Nghiệm của phương trình $\cos x = \cos\dfrac{\pi}{3}$ là:
-
A.
$x = \pm \dfrac{\pi}{4} + k2\pi,k \in {\mathbb{Z}}$.
-
B.
$x = \pm \dfrac{\pi}{6} + k2\pi,k \in {\mathbb{Z}}$.
-
C.
$x = \pm \dfrac{\pi}{2} + k2\pi,k \in {\mathbb{Z}}$.
-
D.
$x = \pm \dfrac{\pi}{3} + k2\pi,k \in {\mathbb{Z}}$.
-
A.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {\dfrac{\pi}{2};\dfrac{3\pi}{2}} \right)$.
-
B.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {\dfrac{- 3\pi}{2}; - \pi} \right)$.
-
C.
Hàm số $y = \text{sin}x$ nghịch biến trên$\left( {\dfrac{- \pi}{2};\dfrac{\pi}{2}} \right)$.
-
D.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {- \dfrac{\pi}{2};0} \right)$.
Cấp số cộng -5; -2; 1; 4;... có công sai là
-
A.
8.
-
B.
3.
-
C.
-3.
-
D.
-5.
Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng số các số hạng bằng 189. Tìm số hạng cuối \({u_6}\) của cấp số nhân đã cho.
-
A.
32
-
B.
104
-
C.
48
-
D.
96
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } \frac{{{2^n} + 1}}{{{3^n}}}\) bằng
-
A.
2
-
B.
1
-
C.
-1
-
D.
0
Cho hàm số $f(x)$ xác định trên ${\mathbb{R}},$ liên tục tại $x = 1$ và thỏa mãn $\lim\limits_{x\rightarrow 1}f(x) = 5.$ Khi đó $f(1)$ bằng bao nhiêu?
-
A.
$f(1) = - 5$.
-
B.
$f(1) = 1$.
-
C.
$f(1) = - 1$.
-
D.
$f(1) = 5$.
Khảo sát thời gian truy cập mạng internet trong ngày của một số học sinh lớp 11 thu được mẫu số liệu ghép nhóm sau:

Số học sinh truy cập mạng trong ngày ít hơn 90 phút trong mẫu số liệu ghép nhóm trên là
-
A.
38.
-
B.
20.
-
C.
7.
-
D.
18.
Cân nặng (kg) của 50 quả mít trong đợt thu hoạch của một trang trại được thống kê trong bảng dưới đây:

Khối lượng trung bình của 50 quả mít trên bằng
-
A.
8,72 kg
-
B.
9,12 kg
-
C.
8,82 kg
-
D.
8,52 kg
Nếu $\lim\limits_{x\rightarrow 3}f(x) = 2$ thì $\lim\limits_{x\rightarrow 3}\left\lbrack {4x - 3f(x)} \right\rbrack$ bằng
-
A.
$2$.
-
B.
$- 1$.
-
C.
$3$.
-
D.
$6$.
Cho hình chóp S.ACBD có đáy ABCD là hình thang có đáy lớn AB. Gọi M là trung điểm của SC. Giao điểm của BC với mặt phẳng (ADM) là:
-
A.
Giao điểm của BC và DM.
-
B.
Giao điểm của BC và AM.
-
C.
Giao điểm của BC và AD.
-
D.
Giao điểm của BC và SD.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA và SC. Đường thẳng MN song song với đường thẳng nào dưới đây?
-
A.
BC.
-
B.
BD.
-
C.
AB.
-
D.
AC.
Cho mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây là đúng?
-
A.
Qua A có đúng một mặt phẳng song song với (P).
-
B.
Qua A có vô số mặt phẳng song song với (P).
-
C.
Qua A không có mặt phẳng nào song song với (P).
-
D.
Qua A có đúng hai mặt phẳng song song với (P).
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} - 3x + 2}}{{x - 2}}}\\1\end{array}} \right.\) \(\begin{array}{*{20}{l}}{khi}\\{khi}\end{array}\) \(\begin{array}{*{20}{l}}{x \ne 2}\\{x = 2}\end{array}\).
a) Giá trị của \(f(2)\) bằng 1.
b) Giá trị của \(\mathop {\lim }\limits_{x \to 2} f(x)\) bằng -1.
c) Hàm số đã cho liên tục trên \(\mathbb{R}\).
d) Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}}\) bằng 1.
Cho hình chóp $S.ABCD$ có đáy là hình thang, $AB\,\text{//}\, CD$ và $AB = 2CD$, O là giao điểm của hai đường thẳng AC và BD. Gọi $M$, $N$ lần lượt là trung điểm $SA$ và $SB$.
a) $AB\,\text{//}\, MC$.
b) Tứ giác CDMN là hình thang cân.
c) E là trung điểm của SC, G là trọng tâm của tam giác SBC, khi đó OG song song với DE.
d) Giao tuyến của (CDE) và (SAC) là đường thẳng EO.
Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian (làm tròn kết quả đến hàng phần trăm)?
Một ruộng bậc thang có thửa thấp nhất (bậc thứ nhất) nằm ở độ cao 950 m so với mực nước biểu, độ chênh lệch giữa thửa trên và thửa dưới trung bình là 1,5 m. Hỏi thửa ruộng ở bậc thứ 12 có độ cao là bao nhiêu mét so với mực nước biển (kết quả làm tròn đến hàng đơn vị)?
Một cơ sở sản xuất bếp gas, tính chi phí sản xuất x (sản phẩm) xác định bởi hàm số: C(x) = 200 + 120x (ngàn đồng). Chi phí trung bình để sản xuất một sản phẩm bằng bao nhiêu ngàn đồng nếu sản xuất số lượng lớn (xem như $t \to +\infty$)?
Khảo sát số lần sử dụng Facebook của một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:

Tìm mốt của mẫu số liệu ghép nhóm trên?
Lời giải và đáp án
Nghiệm của phương trình $\cos x = \cos\dfrac{\pi}{3}$ là:
-
A.
$x = \pm \dfrac{\pi}{4} + k2\pi,k \in {\mathbb{Z}}$.
-
B.
$x = \pm \dfrac{\pi}{6} + k2\pi,k \in {\mathbb{Z}}$.
-
C.
$x = \pm \dfrac{\pi}{2} + k2\pi,k \in {\mathbb{Z}}$.
-
D.
$x = \pm \dfrac{\pi}{3} + k2\pi,k \in {\mathbb{Z}}$.
Đáp án : D
\(\cos x = m \Leftrightarrow \cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - a + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
\(\cos x = \cos \frac{\pi }{3} \Leftrightarrow x = \pm \frac{\pi }{3} + k2\pi \), \(k \in \mathbb{Z}\).
-
A.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {\dfrac{\pi}{2};\dfrac{3\pi}{2}} \right)$.
-
B.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {\dfrac{- 3\pi}{2}; - \pi} \right)$.
-
C.
Hàm số $y = \text{sin}x$ nghịch biến trên$\left( {\dfrac{- \pi}{2};\dfrac{\pi}{2}} \right)$.
-
D.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {- \dfrac{\pi}{2};0} \right)$.
Đáp án : D
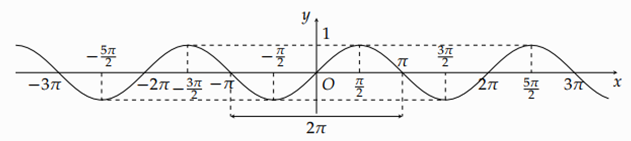
Hàm số đồng biến trên khoảng đồ thị đi lên từ trái sang.
Hàm số $y = \text{sin}x$ đồng biến trên$\left( {- \dfrac{\pi}{2};0} \right)$.
Cấp số cộng -5; -2; 1; 4;... có công sai là
-
A.
8.
-
B.
3.
-
C.
-3.
-
D.
-5.
Đáp án : B
Tính \(d = {u_{n + 1}} - {u_n}\).
Ta có d = 4 - 1 = 1 - (-2) = -2 - (-5) = 3. Vậy công sai bằng 3.
Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng số các số hạng bằng 189. Tìm số hạng cuối \({u_6}\) của cấp số nhân đã cho.
-
A.
32
-
B.
104
-
C.
48
-
D.
96
Đáp án : D
Cấp số nhân \(\left( {{u_n}} \right)\) công bội \(q \ne 1\).
Khi đó tổng \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\).
Công thức số hạng tổng quát của cấp số nhân: \(u_n = u_1 .q^{n-1}\).
\(\left\{ {\begin{array}{*{20}{l}}{q = 2}\\{{S_6} = 189 = {u_1}.\frac{{1 - {q^6}}}{{1 - q}}}\end{array}} \right. \Rightarrow \left\{ \begin{array}{l}q = 2\\{u_1} = 3\end{array} \right.\)
\({u_6} = {u_1}{q^5} = {3.2^5} = 96\).
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } \frac{{{2^n} + 1}}{{{3^n}}}\) bằng
-
A.
2
-
B.
1
-
C.
-1
-
D.
0
Đáp án : D
Chia cả tử và mẫu cho \({3^n}\).
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{{2^n} + 1}}{{{3^n}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{{\left( {\frac{2}{3}} \right)}^n} + {{\left( {\frac{1}{3}} \right)}^n}}}{1} = 0\).
Cho hàm số $f(x)$ xác định trên ${\mathbb{R}},$ liên tục tại $x = 1$ và thỏa mãn $\lim\limits_{x\rightarrow 1}f(x) = 5.$ Khi đó $f(1)$ bằng bao nhiêu?
-
A.
$f(1) = - 5$.
-
B.
$f(1) = 1$.
-
C.
$f(1) = - 1$.
-
D.
$f(1) = 5$.
Đáp án : D
Hàm số f(x) liên tục tại \({x_0}\) khi \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = a\) và \(f({x_0}) = a\).
Vì \(\mathop {\lim }\limits_{x \to 1} f(x) = 5\) và hàm số f(x) liên tục tại x = 1 nên f(1) = 5.
Khảo sát thời gian truy cập mạng internet trong ngày của một số học sinh lớp 11 thu được mẫu số liệu ghép nhóm sau:

Số học sinh truy cập mạng trong ngày ít hơn 90 phút trong mẫu số liệu ghép nhóm trên là
-
A.
38.
-
B.
20.
-
C.
7.
-
D.
18.
Đáp án : A
Đọc bảng số liệu.
Số học sinh truy cập mạng trong ngày ít hơn 90 phút trong mẫu số liệu ghép nhóm trên là:
5 + 13 + 20 = 38.
Cân nặng (kg) của 50 quả mít trong đợt thu hoạch của một trang trại được thống kê trong bảng dưới đây:

Khối lượng trung bình của 50 quả mít trên bằng
-
A.
8,72 kg
-
B.
9,12 kg
-
C.
8,82 kg
-
D.
8,52 kg
Đáp án : A
Tính trung bình của mẫu số liệu ghép nhóm.
Số trung bình của mẫu số liệu là:
\(\bar x = \frac{{6.5 + 12.7 + 19.9 + 9.11 + 4.13}}{{6 + 12 + 19 + 9 + 4}} = 8,72\).
Nếu $\lim\limits_{x\rightarrow 3}f(x) = 2$ thì $\lim\limits_{x\rightarrow 3}\left\lbrack {4x - 3f(x)} \right\rbrack$ bằng
-
A.
$2$.
-
B.
$- 1$.
-
C.
$3$.
-
D.
$6$.
Đáp án : D
Áp dụng các tính chất của giới hạn hàm số.
\(\mathop {\lim }\limits_{x \to 3} \left[ {4x - 3f(x)} \right] = \mathop {4\lim }\limits_{x \to 3} x - 3\mathop {\lim }\limits_{x \to 3} f(x) = 4.3 - 3.2 = 6\).
Cho hình chóp S.ACBD có đáy ABCD là hình thang có đáy lớn AB. Gọi M là trung điểm của SC. Giao điểm của BC với mặt phẳng (ADM) là:
-
A.
Giao điểm của BC và DM.
-
B.
Giao điểm của BC và AM.
-
C.
Giao điểm của BC và AD.
-
D.
Giao điểm của BC và SD.
Đáp án : C
Tìm điểm cùng thuộc đường thẳng và mặt phẳng.
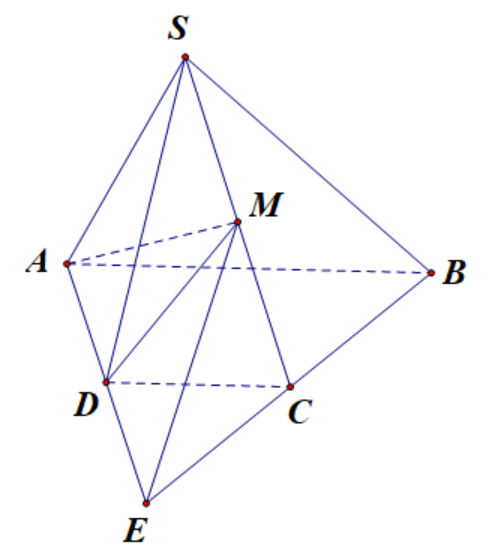
Gọi E là giao điểm của AD và BC.
Vì E thuộc AD nên E thuộc (AMD), mà E thuộc BC, do đó E là giao điểm của BC và (AMD).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA và SC. Đường thẳng MN song song với đường thẳng nào dưới đây?
-
A.
BC.
-
B.
BD.
-
C.
AB.
-
D.
AC.
Đáp án : D
Dựa vào tính chất đường trung bình trong tam giác.
Vì MN là đường trung bình của tam giác SAC nên MN // AC.
Cho mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây là đúng?
-
A.
Qua A có đúng một mặt phẳng song song với (P).
-
B.
Qua A có vô số mặt phẳng song song với (P).
-
C.
Qua A không có mặt phẳng nào song song với (P).
-
D.
Qua A có đúng hai mặt phẳng song song với (P).
Đáp án : A
Dựa vào lí thuyết hai mặt phẳng song song.
Qua một điểm nằm ngoài mặt phẳng, có duy nhất một mặt phẳng song song với mặt phẳng đó.
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} - 3x + 2}}{{x - 2}}}\\1\end{array}} \right.\) \(\begin{array}{*{20}{l}}{khi}\\{khi}\end{array}\) \(\begin{array}{*{20}{l}}{x \ne 2}\\{x = 2}\end{array}\).
a) Giá trị của \(f(2)\) bằng 1.
b) Giá trị của \(\mathop {\lim }\limits_{x \to 2} f(x)\) bằng -1.
c) Hàm số đã cho liên tục trên \(\mathbb{R}\).
d) Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}}\) bằng 1.
a) Giá trị của \(f(2)\) bằng 1.
b) Giá trị của \(\mathop {\lim }\limits_{x \to 2} f(x)\) bằng -1.
c) Hàm số đã cho liên tục trên \(\mathbb{R}\).
d) Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}}\) bằng 1.
Tính biểu thức \(f(x)\) tại \(x = 2\).
Tính \(\mathop {\lim }\limits_{x \to 2} f(x)\), xét tính liên tục của hàm số.
a) Đúng. Khi \(x = 2\) thì \(f(x) = 1\). Do đó \(f(2) = 1\).
b) Sai. Có \(\mathop {\lim }\limits_{x \to 2} f(x) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x + 2}}{{x - 2}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)(x - 1)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} (x - 1) = 2 - 1 = 1\).
c) Đúng. Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to 2} f(x) = 1}\\{f(2) = 1}\end{array}} \right.\) suy ra \(\mathop {\lim }\limits_{x \to 2} f(x) = f(2) = 1\).
Vậy hàm số liên tục trên \(\mathbb{R}\).
d) Sai. Khi \(x \ne 2\) thì \(f(x) = \frac{{{x^2} - 3x + 2}}{{x - 2}} = x - 1\) nên ta có:
\(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {x(x - 1) + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {{x^2} - x + 1} }}{{x + 1}}\)
\( = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {{x^2}\left( {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} \right)} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\left| x \right|\sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{ - x\sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x + 1}} = {\rm{\;}} - 1\).
Cho hình chóp $S.ABCD$ có đáy là hình thang, $AB\,\text{//}\, CD$ và $AB = 2CD$, O là giao điểm của hai đường thẳng AC và BD. Gọi $M$, $N$ lần lượt là trung điểm $SA$ và $SB$.
a) $AB\,\text{//}\, MC$.
b) Tứ giác CDMN là hình thang cân.
c) E là trung điểm của SC, G là trọng tâm của tam giác SBC, khi đó OG song song với DE.
d) Giao tuyến của (CDE) và (SAC) là đường thẳng EO.
a) $AB\,\text{//}\, MC$.
b) Tứ giác CDMN là hình thang cân.
c) E là trung điểm của SC, G là trọng tâm của tam giác SBC, khi đó OG song song với DE.
d) Giao tuyến của (CDE) và (SAC) là đường thẳng EO.
Áp dụng tính chất của hình thang, đường trung bình, định lí Thales để chứng minh hai đường thẳng song song.

a) Sai. AB không song song với MC.
b) Sai. MN // AB và \(MN = \frac{1}{2}AB\) theo tính chất đường trung bình trong tam giác.
Mà DC // AB và \(DC = \frac{1}{2}AB\) theo giả thiết.
Do đó MN // DC và MN = DC. Suy ra CDMN là hình bình hành.
c) Đúng. Vì G là trọng tâm tam giác SBC nên \(\frac{{BG}}{{GE}} = 2\).
Theo định lí Thales, vì DC // AB nên \(\frac{{BD}}{{OD}} = \frac{{AB}}{{DC}} = 2\).
Vì \(\frac{{BG}}{{GE}} = \frac{{BD}}{{OD}} = 2\) nên theo định lí Thales đảo, suy ra OG // DE.
d) Sai. Vì O không thuộc (CDE) nên EO không phải giao tuyến của (CDE) và (SAC).
Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian (làm tròn kết quả đến hàng phần trăm)?
Tìm số đo góc lượng giác quạt quay được trong 1 giây, từ đó tính số đo góc lượng giác quạt quay được trong 3 giây.
Tốc độ góc của quạt trần là: \(\frac{{45 \cdot 2\pi }}{{60}} = \frac{{3\pi }}{2}\) (rad/s).
Sau 3 giây, quạt quay được một góc có số đo là:
\(\frac{{3\pi }}{2} \cdot 3 = \frac{{9\pi }}{2} \approx 14,1\) (rad).
Một ruộng bậc thang có thửa thấp nhất (bậc thứ nhất) nằm ở độ cao 950 m so với mực nước biểu, độ chênh lệch giữa thửa trên và thửa dưới trung bình là 1,5 m. Hỏi thửa ruộng ở bậc thứ 12 có độ cao là bao nhiêu mét so với mực nước biển (kết quả làm tròn đến hàng đơn vị)?
Áp dụng công thức số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} + (n - 1)d\).
Kí hiệu $u_n$ là chiều cao so với mực nước biển của thửa ruộng ở bậc thứ n.
Khi đó, dãy số $(u_n)$ là một cấp số cộng với $u_1 = 950$ và d = 1,5.
Ta có: $u_{12} = u_1 + 11d = 950 + 11 . 1,5 = 966,5$.
Vậy thửa ruộng ở bậc thứ 12 có độ cao xấp xỉ 967 m so với mực nước biển.
Một cơ sở sản xuất bếp gas, tính chi phí sản xuất x (sản phẩm) xác định bởi hàm số: C(x) = 200 + 120x (ngàn đồng). Chi phí trung bình để sản xuất một sản phẩm bằng bao nhiêu ngàn đồng nếu sản xuất số lượng lớn (xem như $t \to +\infty$)?
Lập hàm chi phí trung bình $\overline{C}(x)$ và tính $\lim_{x \to +\infty} \overline{C}(x)$.
Gọi $\overline{C}(x)$ là chi phí trung bình để sản xuất một sản phẩm.
$\overline{C}(x) = \frac{C(x)}{x} = \frac{200 + 120x}{x} $.
$\lim_{x \to +\infty} \overline{C}(x) = \lim_{x \to +\infty} \frac{200 + 120x}{x} = 120$ (ngàn đồng).
Khảo sát số lần sử dụng Facebook của một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:

Tìm mốt của mẫu số liệu ghép nhóm trên?
Hiệu chỉnh mẫu số liệu và áp dụng công thức tính mốt của mẫu số liệu ghép nhóm:
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g\).
Do số lần sử dụng Facebook là số nguyên nên ta chỉnh lại như sau:

Nhóm chứa mốt là [8,5; 11,5) do đó:
$u_m = 8,5; n_{m-1} = 5; n_{m+1} = 8; u_{m+1} - u_m = 11,5 - 8,5 = 3$.
Mốt của mẫu số liệu ghép nhóm là:
$M_o = 8,5 + \frac{11 - 5}{(11 - 5) + (11 - 8)} . 3 = 10,5$.
Xác định số hạng đầu và công bội của cấp số nhân, áp dụng công thức ${{u}_{n}}={{u}_{1}}{{q}^{n-1}}$.
Áp dụng quy tắc tính giới hạn của hàm số.
a) Theo đề bài ta có, $h_n = \frac{1}{4} h_{n-1}$ nên $(h_n)$ là một cấp số nhân với $h_1 = \frac{1}{4} . 100 = 25$ và công bội $q = \frac{1}{4}$.
Suy ra số hạng tổng quát của dãy số $(h_n)$: $h_n = u_1 q^{n-1} = 25 . \left( \frac{1}{4} \right)^{n-1} = \frac{100}{4^n}$.
b) Ta có: $\lim h_n = \lim \frac{100}{4^n} = \lim \left( 100 . \frac{1}{4^n} \right) = \lim 100 . \lim \left( \frac{1}{4} \right)^n = 100 . 0 = 0$.
Từ giới hạn đó, ta rút ra được ý nghĩa: Khi $n$ càng dần tới vô cực thì độ cao của quả bóng đạt được sau khi nảy ngày càng nhỏ và độ cao đó dần tới 0.
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
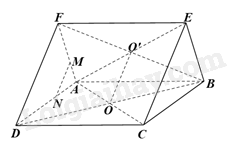
a) Vì O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.
Vì O là trung điểm của BD, O’ là trung điểm của BF nên OO’ là đường trung bình của tam giác BDF. Do đó, OO’//DF (1)
Vì O là trung điểm của AC, O’ là trung điểm của AE nên OO’ là đường trung bình của tam giác ACE. Do đó, OO’//CE (2)
Từ (1) và (2) ta có: OO’//DF//CE
Vì OO’//DF, OO’ không nằm trên mặt phẳng (ADF) và \(DF \subset \left( {ADF} \right)\) nên OO’//(ADF).
Vì OO’//CE, OO’ không nằm trên mặt phẳng (BCE) và \(CE \subset \left( {BCE} \right)\) nên OO’//(BCE).
b) Vì \(AM = \frac{1}{3}AF,AN = \frac{1}{3}AD \Rightarrow \frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\)
Tam giác ADF có: \(\frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\) nên MN//DF (định lí Thalès đảo)
Vì MN//DF, MN không nằm trên mặt phẳng (DCEF) và \(DF \subset \left( {DCEF} \right)\) nên MN//(DCEF).
Để tính tứ phân vị thứ nhất Q1 của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa Q1, giả sử đó là nhóm thứ \(p:\left[ {{a_p};{a_{p + 1}}} \right).\) Khi đó,
\({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right),\)
Trong đó, n là cỡ mẫu, mp là tần số nhóm p, với p = 1 ta quy ước m1 +…+ mp-1 = 0.
Dựa trên mẫu số liệu trên, chúng ta có thể tính tổng số hộ gia đình trong địa phương này là 8 + 17 + 35 + 56 + 27 + 15 = 158.
Nhóm chứa tứ phân vị thứ nhất là nhóm thứ ba \(\left( {8;11} \right],\) với \(j = 3.\) Ta có
\({a_3} = 8,{h_3} = 3,{m_3} = 35,m \le 8 + 17 = 25,r = 1.\)
Do đó, tứ phân vị thứ nhất là:
\({Q_1} = 8 + \frac{{\frac{{158}}{4} - 25}}{{35}}.3 \approx 9,24\)
Doanh nghiệp sẽ hỗ trợ các hộ gia đình có thu nhập dưới 9,24 triệu đồng.
Đề thi học kì 1 Toán 11 - Đề số 10
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
Phần trắc nghiệm (7 điểm) Câu 1: Nghiệm của phương trình
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (7 điểm) Câu 1: Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là
A. Nội dung ôn tập Hàm số lượng giác và phương trình lượng giác 1. Giá trị lượng giác của góc lượng giác 2. Công thức lượng giác 3. Hàm số lượng giác 4. Phương trình lượng giác cơ bản
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |











Danh sách bình luận