Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 6
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Đề bài
Mệnh đề nào sau đây đúng?
-
A.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\)
-
B.
Số đo của góc nhị diện nhận giá trị từ \({90^o}\) đến \({180^o}\)
-
C.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({90^o}\)
-
D.
Hai mặt phẳng cắt nhau tạo thành hai góc nhị diện
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mệnh đề nào sau đây đúng?
-
A.
(SB,CD) = (SB,AD)
-
B.
(SB,CD) = (SC,CD)
-
C.
(SB,CD) = (SD,CD)
-
D.
(SB,CD) = (SB,AB)
Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng (P). Mệnh đề nào sau đây
đúng?
-
A.
Nếu \(a \bot c\) và \(b \bot c\) thì a // b
-
B.
Nếu \(a \bot b\) và \(b \bot c\) thì \(a \bot c\)
-
C.
Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau
-
D.
Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P)
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai mặt phẳng (ABCD) và (A’B’C’D’) bằng
-
A.
\(a\sqrt 2 \)
-
B.
\(\frac{a}{3}\)
-
C.
\(a\)
-
D.
\(\frac{a}{2}\)
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là
-
A.
\(V = \frac{1}{3}\pi {B^2}h\)
-
B.
\(V = \frac{1}{3}Bh\)
-
C.
\(V = \frac{\pi }{3}Bh\)
-
D.
\(V = Bh\)
Với a là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
-
A.
\({a^{\frac{5}{2}}}\)
-
B.
\(a\)
-
C.
\({a^{\frac{3}{2}}}\)
-
D.
\({a^{\frac{1}{4}}}\)
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
-
A.
\(\frac{5}{{2a}}\)
-
B.
\(\frac{{5a}}{2}\)
-
C.
\(\frac{2}{{5a}}\)
-
D.
\(\frac{{2a}}{5}\)
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
-
A.
\(y = {\left( {\frac{1}{e}} \right)^x}\)
-
B.
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\)
-
C.
\(y = {\left( {\frac{1}{3}} \right)^x}\)
-
D.
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\)
Tập nghiệm S của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}}\) là
-
A.
\(S = \left( { - \infty ;1} \right)\)
-
B.
\(S = \left( { - \infty ;2} \right)\)
-
C.
\(S = \left( {2; + \infty } \right)\)
-
D.
\(S = \left( {1; + \infty } \right)\)
Tìm tập xác định D của hàm số \({\log _2}\left( {{x^2} - 2x - 3} \right)\).
-
A.
\(D = \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
-
B.
\(D = \left[ { - 1;3} \right]\)
-
C.
(D = \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
-
D.
\(D = \left( { - 1;3} \right)\)
Rút gọn biểu thức \(P = {x^2}.\sqrt[3]{x}\), x > 0.
-
A.
\(P = {x^{\frac{4}{3}}}\)
-
B.
\(P = {x^{\frac{5}{3}}}\)
-
C.
\(P = {x^{\frac{7}{3}}}\)
-
D.
\(P = {x^{\frac{8}{3}}}\)
-
A.
\(y = {\log _{\frac{1}{2}}}x\)
-
B.
\(y = {\log _2}x\)
-
C.
\(y = {2^x}\)
-
D.
\(y = {\left( {\frac{1}{2}} \right)^x}\)
Cho phương trình \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1\) (*).
a) Điều kiện: x > 1.
b) Gọi x = a là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
c) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}\): 2x – y – 8 = 0 với \({d_2}\): y = 0.
d) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và \(SA \bot (ABCD)\). Gọi M và N lần lượt là hình chiếu của điểm A trên các đường thẳng SB và SD.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
Năng lượng giải tỏa E của một trận động đất tại tâm địa chấn ở M độ Richte được xác định bởi
công thức log(E) = 11,4 + 1,5M. Vào năm 1995, Thành phố X xảy ra một trận động đất 8 độ Richte và năng lượng giải tỏa tại tâm địa chấn của nó gấp 14 lần trận động đất xảy ra tại thành phố Y vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố Y là bao nhiêu độ Richte (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Kim tự tháp có hình dạng là một khối chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 230 m, độ dài cạnh bên bằng 214 m. Tính khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp (kết quả làm tròn đến hàng đơn vị).
Đáp án:
Số lượng loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức \(s(t) = s(0){.2^t}\), trong đó s(0) là số lượng vi khuẩn A lúc ban đầu, s(t) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu kể từ lúc ban đầu, số lượng loại vi khuẩn A là 20 triệu con?
Đáp án:
Cho một chậu nước hình chóp cụt đều (hình vẽ) có chiều cao bằng 3 dm, đáy là lục giác đều, độ dài cạnh đáy lớn bằng 2 dm và độ dài cạnh đáy nhỏ bằng 1 dm. Tính thể tích của chậu nước (tính chính xác đến hàng phần mười của \(d{m^3}\)).

Đáp án:
Lời giải và đáp án
Mệnh đề nào sau đây đúng?
-
A.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\)
-
B.
Số đo của góc nhị diện nhận giá trị từ \({90^o}\) đến \({180^o}\)
-
C.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({90^o}\)
-
D.
Hai mặt phẳng cắt nhau tạo thành hai góc nhị diện
Đáp án : A
Dựa vào lý thuyết góc nhị diện.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mệnh đề nào sau đây đúng?
-
A.
(SB,CD) = (SB,AD)
-
B.
(SB,CD) = (SC,CD)
-
C.
(SB,CD) = (SD,CD)
-
D.
(SB,CD) = (SB,AB)
Đáp án : D
Nếu a // b thì (a,c) = (b,c).
Vì AB // CD nên (SB,CD) = (SB,AB).
Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng (P). Mệnh đề nào sau đây
đúng?
-
A.
Nếu \(a \bot c\) và \(b \bot c\) thì a // b
-
B.
Nếu \(a \bot b\) và \(b \bot c\) thì \(a \bot c\)
-
C.
Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau
-
D.
Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P)
Đáp án : C
Dựa vào quan hệ song song và vuông góc trong không gian.
Xét phương án A: Nếu \(a \bot c\) và \(b \bot c\) thì a, b có thể vuông góc, cắt nhau hoặc chéo nhau hoặc song song. Vậy A sai.
Xét phương án B: Nếu \(a \bot b\) và \(b \bot c\) thì a, b có thể vuông góc, cắt nhau hoặc chéo nhau hoặc song song. Vậy B sai.
Xét phương án C: Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau. Vậy C đúng.
Xét phương án D: Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P) hoặc \(a \subset (P)\). Vậy A sai.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai mặt phẳng (ABCD) và (A’B’C’D’) bằng
-
A.
\(a\sqrt 2 \)
-
B.
\(\frac{a}{3}\)
-
C.
\(a\)
-
D.
\(\frac{a}{2}\)
Đáp án : C
Đưa về tính khoảng cách từ một điểm đến một mặt phẳng.
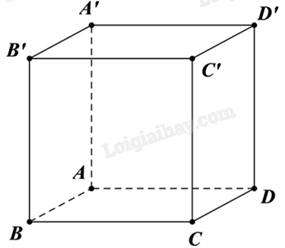
Vì (ABCD) // (A’B’C’D’) nên \(d\left( {(ABCD),(A'B'C'D')} \right) = d\left( {A,(A'B'C'D')} \right)\).
Mặt khác, A’ là hình chiếu vuông góc của A lên (A’B’C’D’) nên \(d\left( {A,(A'B'C'D')} \right) = AA'\).
Vậy \(d\left( {(ABCD),(A'B'C'D')} \right) = AA' = a\).
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là
-
A.
\(V = \frac{1}{3}\pi {B^2}h\)
-
B.
\(V = \frac{1}{3}Bh\)
-
C.
\(V = \frac{\pi }{3}Bh\)
-
D.
\(V = Bh\)
Đáp án : B
Áp dụng công thức tính thể tích khối chóp.
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là \(V = \frac{1}{3}Bh\).
Với a là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
-
A.
\({a^{\frac{5}{2}}}\)
-
B.
\(a\)
-
C.
\({a^{\frac{3}{2}}}\)
-
D.
\({a^{\frac{1}{4}}}\)
Đáp án : A
Áp dụng tính chất của lũy thừa \({a^m}.{a^n} = {a^{m + n}}\).
\({a^2}.{a^{\frac{1}{2}}} = {a^{2 + \frac{1}{2}}} = {a^{\frac{5}{2}}}\).
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
-
A.
\(\frac{5}{{2a}}\)
-
B.
\(\frac{{5a}}{2}\)
-
C.
\(\frac{2}{{5a}}\)
-
D.
\(\frac{{2a}}{5}\)
Đáp án : A
Áp dụng công thức \({\log _{{a^m}}}b = \frac{1}{m}{\log _a}b\) và \({\log _a}{b^m} = m{\log _a}b\).
\({\log _{25}}32 = {\log _{{5^2}}}{2^5} = \frac{5}{2}{\log _5}2 = \frac{5}{{2{{\log }_2}5}} = \frac{5}{{2a}}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
-
A.
\(y = {\left( {\frac{1}{e}} \right)^x}\)
-
B.
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\)
-
C.
\(y = {\left( {\frac{1}{3}} \right)^x}\)
-
D.
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\)
Đáp án : D
Hàm số \(y = {a^x}\) đồng biến khi a > 1.
Vì \(\sqrt[{2024}]{\pi } > 1\) nên \(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\) đồng biến trên tập xác định.
Tập nghiệm S của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}}\) là
-
A.
\(S = \left( { - \infty ;1} \right)\)
-
B.
\(S = \left( { - \infty ;2} \right)\)
-
C.
\(S = \left( {2; + \infty } \right)\)
-
D.
\(S = \left( {1; + \infty } \right)\)
Đáp án : D
Đưa hai vế của bất phương trình về cùng cơ số.
\({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}} \Leftrightarrow {5^{x + 2}} < {\left( {{5^{ - 3}}} \right)^{ - x}} \Leftrightarrow {5^{x + 2}} < {5^{3x}} \Leftrightarrow x + 2 < 3x \Leftrightarrow x > 1\).
Tìm tập xác định D của hàm số \({\log _2}\left( {{x^2} - 2x - 3} \right)\).
-
A.
\(D = \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
-
B.
\(D = \left[ { - 1;3} \right]\)
-
C.
(D = \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
-
D.
\(D = \left( { - 1;3} \right)\)
Đáp án : C
Điều kiện xác định của hàm \({\log _a}x\) là x > 0.
ĐKXĐ: \({x^2} - 2x - 3 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 3\\x < - 1\end{array} \right.\). Vậy \(D = \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\).
Rút gọn biểu thức \(P = {x^2}.\sqrt[3]{x}\), x > 0.
-
A.
\(P = {x^{\frac{4}{3}}}\)
-
B.
\(P = {x^{\frac{5}{3}}}\)
-
C.
\(P = {x^{\frac{7}{3}}}\)
-
D.
\(P = {x^{\frac{8}{3}}}\)
Đáp án : C
Áp dụng công thức \({x^m}.{x^n} = {x^{m + n}}\), \(\sqrt[b]{{{x^a}}} = {x^{\frac{a}{b}}}\).
\(P = {x^2}.\sqrt[3]{x} = {x^2}.{x^{\frac{1}{3}}} = {x^{2 + \frac{1}{3}}} = {x^{\frac{7}{3}}}\).
-
A.
\(y = {\log _{\frac{1}{2}}}x\)
-
B.
\(y = {\log _2}x\)
-
C.
\(y = {2^x}\)
-
D.
\(y = {\left( {\frac{1}{2}} \right)^x}\)
Đáp án : B
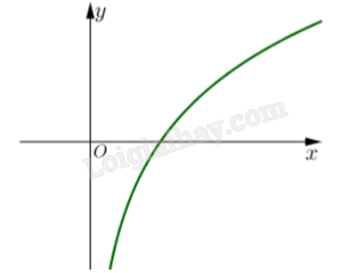
Dựa vào điểm đồ thị đi qua và xét sự đồng biến, nghịch biến.
Vì đồ thị hàm số đi qua điểm có tọa độ (1;0) và x > 0 nên đây là hàm số logarit có dạng \(y = {\log _a}x\).
Đồ thị đi lên từ trái sang nên hàm số đồng biến trên \((0; + \infty )\). Do đó, a > 1.
Cho phương trình \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1\) (*).
a) Điều kiện: x > 1.
b) Gọi x = a là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
c) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}\): 2x – y – 8 = 0 với \({d_2}\): y = 0.
d) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
a) Điều kiện: x > 1.
b) Gọi x = a là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
c) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}\): 2x – y – 8 = 0 với \({d_2}\): y = 0.
d) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
Giải các phương trình rồi so sánh tập nghiệm.
a) Đúng. Điều kiện: \(\left\{ \begin{array}{l}x + 6 > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 6\\x > 1\end{array} \right. \Leftrightarrow x > 1\).
b) Sai. \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1 \Leftrightarrow {\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + {\log _3}3\)
\( \Leftrightarrow {\log _3}\left( {x + 6} \right) = {\log _3}3\left( {x - 1} \right) \Leftrightarrow x + 6 = 3\left( {x - 1} \right) \Leftrightarrow x = \frac{9}{2}\) (TMĐK).
Ta có \(\mathop {\lim }\limits_{x \to \frac{9}{2}} \left( {x - 3} \right) = \frac{9}{2} - 3 = \frac{3}{2}\).
c) Sai. Hoành độ giao điểm của \({d_1}\) và \({d_2}\) là nghiệm của phương trình \(2x - 8 = 0 \Leftrightarrow x = 4\).
Vậy hoành độ giao điểm của \({d_1}\) và \({d_2}\) không là nghiệm của (*).
d) Sai. \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0 \Leftrightarrow {x^2} - 11x + 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11 + \sqrt {85} }}{2}\\x = \frac{{11 - \sqrt {85} }}{2}\end{array} \right.\).
Vậy phương trình (*) không có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và \(SA \bot (ABCD)\). Gọi M và N lần lượt là hình chiếu của điểm A trên các đường thẳng SB và SD.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
Áp dụng điều kiện để đường thẳng vuông góc với mặt phẳng; quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
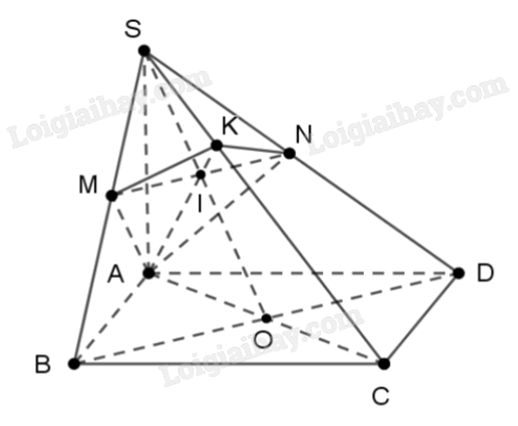
a) Đúng. Vì \(SA \bot (ABCD)\), mà \(AO \subset (ABCD)\) nên \(SA \bot AO\).
b) Sai. Giả sử \(AC \bot (SBD)\), khi đó \(AC \bot SO\). Điều đó vô lí vì \(AC \bot SA\).
c) Sai. Vì \(SA \bot (ABCD)\) nên \(SA \bot BC\). Mặt khác, vì ABCD là hình vuông nên \(AB \bot BC\).
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AM\).
Lại có \(\left\{ \begin{array}{l}BC \bot AM\\SB \bot AM\end{array} \right. \Rightarrow AM \bot (SBC)\).
d) Đúng. Hai tam giác vuông SAB và SAD bằng nhau có các đường cao tương ứng là AM và AN nên BM = DN.
Mặt khác tam giác SBD cân tại đỉnh S nên MN // BD.
Do ABCD là hình vuông nên \(AC \bot BD\), mà \(SA \bot BD\) nên \(BD \bot (SAC)\).
Vì MN // BD nên \(MN \bot (SAC) \Rightarrow MN \bot AK\).
Năng lượng giải tỏa E của một trận động đất tại tâm địa chấn ở M độ Richte được xác định bởi
công thức log(E) = 11,4 + 1,5M. Vào năm 1995, Thành phố X xảy ra một trận động đất 8 độ Richte và năng lượng giải tỏa tại tâm địa chấn của nó gấp 14 lần trận động đất xảy ra tại thành phố Y vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố Y là bao nhiêu độ Richte (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Thay các giá trị từ đề bài vào công thức đã cho. Áp dụng quy tắc biến đổi phương trình logarit.
Năng lượng giải tỏa của trận động đất ở thành phố X là \({E_X} = {10^{11,4 + 1,5.8}} = {10^{23,4}}\).
Theo đề bài, ta có năng lượng giải tỏa của trận động đất ở thành phố Y là \({E_Y} = \frac{{{E_1}}}{{14}} = \frac{{{{10}^{23,4}}}}{{14}}\).
Độ lớn của trận động đất ở thành phố Y là:
\(\log ({E_Y}) = 11,4 + 1,5{M_Y} \Rightarrow M = \frac{{\log ({E_Y}) - 11,4}}{{1,5}} = \frac{{\log \left( {\frac{{{{10}^{23,4}}}}{{14}}} \right) - 11,4}}{{1,5}} \approx 7,2\) độ Richte.
Kim tự tháp có hình dạng là một khối chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 230 m, độ dài cạnh bên bằng 214 m. Tính khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp (kết quả làm tròn đến hàng đơn vị).
Đáp án:
Đáp án:
Khoảng cách từ một điểm đến một mặt phẳng là khoảng cách từ hình chiếu vuông góc của điểm lên mặt phẳng tới điểm đó.
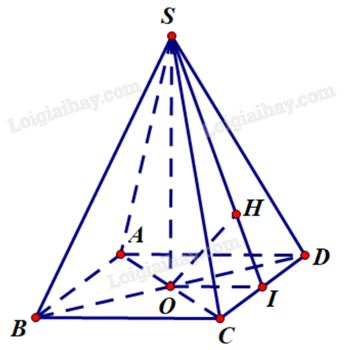
S.ABCD là chóp tứ giác đều nên ABCD là hình vuông.
Giả sử O là tâm hình vuông ABCD, khi đó \(SO \bot (ABCD) \Rightarrow SO \bot CD\).
Gọi I là trung điểm của CD. Khi đó OI // AD (tính chất đường trung bình) và \(CD \bot OI\).
Lấy H thuộc SI sao cho \(OH \bot SI\).
Ta có \(\left\{ \begin{array}{l}CD \bot OI\\CD \bot SO\end{array} \right. \Rightarrow CD \bot (SOI) \Rightarrow CD \bot OH\).
Mặt khác \(\left\{ \begin{array}{l}OH \bot SI\\OH \bot CD\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O,(SCD)} \right) = OH\) (do H thuộc (SCD).
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {S{A^2} - {{\left( {\frac{{AC}}{2}} \right)}^2}} = \sqrt {{{214}^2} - {{\left( {\frac{{230\sqrt 2 }}{2}} \right)}^2}} = \sqrt {19346} \) (m).
\(OH = \frac{1}{{\sqrt {\frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{19346}} + \frac{1}{{{{\left( {\frac{{230}}{2}} \right)}^2}}}} }} \approx 89\) (m).
Vậy khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp xấp xỉ 89 mét.
Số lượng loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức \(s(t) = s(0){.2^t}\), trong đó s(0) là số lượng vi khuẩn A lúc ban đầu, s(t) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu kể từ lúc ban đầu, số lượng loại vi khuẩn A là 20 triệu con?
Đáp án:
Đáp án:
Thay các giá trị từ đề bài vào công thức đã cho. Áp dụng quy tắc biến đổi phương trình mũ.
\(s(3) = s(0){.2^3} \Leftrightarrow 625000 = s(0){.2^3} \Leftrightarrow s(0) = 78125\).
\(20000000 = {78125.2^t} \Leftrightarrow {2^t} = 256 \Leftrightarrow t = 8\).
Cho một chậu nước hình chóp cụt đều (hình vẽ) có chiều cao bằng 3 dm, đáy là lục giác đều, độ dài cạnh đáy lớn bằng 2 dm và độ dài cạnh đáy nhỏ bằng 1 dm. Tính thể tích của chậu nước (tính chính xác đến hàng phần mười của \(d{m^3}\)).

Đáp án:
Đáp án:
Các đáy lục giác đều cạnh a được tạo thành từ 6 tam giác đều cạnh a. Từ đó, tính diện tích hai đáy của khối chóp và áp dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}\pi \left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)\).
\({S_1} = \frac{{{1^2}.\sqrt 3 }}{4}.6 = \frac{{3\sqrt 3 }}{2}\); \({S_2} = \frac{{{2^2}.\sqrt 3 }}{4}.6 = 6\sqrt 3 \); \({S_1}{S_2} = \frac{{3\sqrt 3 }}{2}.6\sqrt 3 = 27\).
\(V = \frac{1}{3}h\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right) = \frac{1}{3}.3\left( {\frac{{3\sqrt 3 }}{2} + 3\sqrt 3 + 6\sqrt 3 } \right) = \frac{{21\sqrt 3 }}{2} \approx 18,2\) \((d{m^3})\).
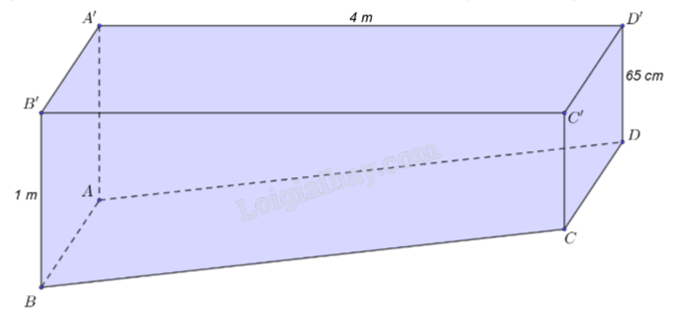
Dựng mặt phẳng (P) theo yêu cầu đề bài. Tính góc giữa (P) và (ABCD) bằng cách đưa về tính góc giữa hai đường thẳng thuộc hai mặt phẳng và vuông góc với giao tuyến của của hai mặt phẳng đó.
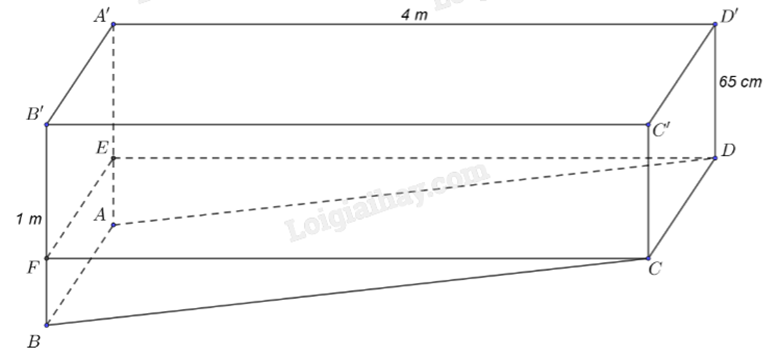
Dựng mặt phẳng hình chữ nhật (CDEF) song song với mặt phẳng (A’B’C’D’) với E thuộc AA’, F thuộc BB’.
Xét hai mặt phẳng (CDEF) và (ABCD) có giao tuyến là CD. Vì CF và CB cùng vuông góc với CD nên \(\left( {CDEF,ABCD} \right) = \left( {CF,CB} \right) = \widehat {FCB}\).
Ta có BB’ = 1 m = 100 cm; B’F = 65 cm; BF = BB’ – B’F = 100 – 65 = 35 cm; CF = 4 m = 400 cm.
Xét tam giác BCF vuông tại F, ta có \(\tan \widehat {FCB} = \frac{{FB}}{{FC}} = \frac{{35}}{{400}} = \frac{7}{{80}} \Rightarrow \widehat {FCB} \approx {5^o}\).
Vậy, bác Minh cần đặt mép BC của khối gỗ tạo với lưỡi cắt của máy cắt một góc xấp xỉ \({5^o}\).
Áp dụng công thức tính lãi kép: \(P = A{\left( {1 + r} \right)^n}\).
Gọi A là số tiền ban đầu gửi tiết kiệm theo thể thức lãi suất kép với lãi suất 8,4%/năm.
Khi đó sau n năm số tiền thu được là \(P = A{\left( {1 + 8,4\% } \right)^n}\).
Để thu được số tiền gấp đôi số tiền ban đầu thì \(2A = A{\left( {1 + 8,4\% } \right)^n} \Leftrightarrow {\left( {1 + 8,4\% } \right)^n} = 2 \Leftrightarrow n = {\log _{1 + 8,4\% }}2 \approx 8,59\) (năm).
Vậy sau ít nhất 9 năm người đó thu được số tiền gấp đôi số tiền ban đầu.
Áp dụng các công thức biến đổi logarit, tính a theo b rồi thay vào biểu thức \({\log _{\frac{a}{{{b^2}}}}}x\) và rút gọn.
\({\log _b}x = 8 \Leftrightarrow x = {b^8}\), mà \(x = {a^2}\) suy ra \({a^2} = {b^8} \Leftrightarrow a = {b^4}\) (vì a > 1).
\({\log _{\frac{a}{{{b^2}}}}}x = {\log _{\frac{{{b^4}}}{{{b^2}}}}}x = {\log _{{b^2}}}x = \frac{1}{2}{\log _b}x = \frac{1}{2}.8 = 4\).
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng. Với a là số thực khác 0 thì:
Phần trắc nghiệm (7 điểm) Câu 1: Khẳng định nào sau đây là đúng?
Phần trắc nghiệm (7 điểm) Câu 1: Cho $a>0,m,n\in \mathbb{R}$. Khẳng định nào sau đây là đúng?
Phần trắc nghiệm (7 điểm) Câu 1: Cho số thực dương a và số hữu tỉ $r=\frac{m}{n}$, trong đó $m,n\in \mathbb{Z},n>0$. Ta có:
Phần trắc nghiệm (7 điểm) Câu 1: Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận