Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, G lần lượt là các điểm thuộc SB, SC sao cho \(\frac{{SM}}{{MB}} = \frac{{SG}}{{GC}} = 2\). Tứ giác MGDA là hình gì?
-
A.
Hình thoi.
-
B.
Hình bình hành.
-
C.
Hình thang.
-
D.
Hình chữ nhật.
Phương pháp giải
Sử dụng kiến thức về tính chất của hai đường thẳng song song: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Lời giải của GV Loigiaihay.com
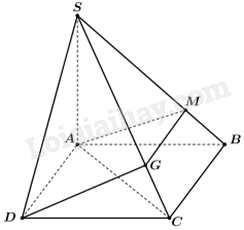
Tam giác SBC có: \(\frac{{SM}}{{MB}} = \frac{{SG}}{{GC}} = 2\) nên MG//BC (định lí Thalès đảo)
Mà BC// AD (Tứ giác ABCD là hình bình hành). Do đó, MG//AD. Suy ra, tứ giác MGDA là hình thang.
Đáp án : C








Danh sách bình luận