Đề kiểm tra giữa học kì 1 Toán 8 - Đề số 3

Làm đề thi

Đề bài

Câu 1 :

Cho hình thang có đáy lớn gấp đôi đáy nhỏ, đáy nhỏ lớn hơn chiều cao $2$ đơn vị. Biểu thức tính diện tích hình thang là:

A.

$S = {3x^2} -6x$
B.

$S = \dfrac{{{3x^2} -6x}}{2}$
C.

$S = \dfrac{{{x^2} + 2x + 4}}{2}$
D.

$S = \dfrac{{{x^2} - 2x - 4}}{2}$

Câu 2 :

Khai triển ${\left( {3x - 4y} \right)^2}$ ta được

A.

$9{x^2} - 24xy + 16{y^2}$
B.

$9{x^2} - 12xy + 16{y^2}$
C.

$9{x^2} - 24xy + 4{y^2}$
D.

$9{x^2} - 6xy + 16{y^2}$

Câu 3 :

Rút gọn biểu thức $B = \left( {2a - 3} \right)\left( {a + 1} \right) - {\left( {a - 4} \right)^2} - a\left( {a + 7} \right)$ ta được

A.

$0$
B.

$1$
C.

$19$
D.

$ - 19$

Câu 4 :

Chọn câu sai.

A.

${A^3} + {B^3} $$ = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)$
B.

${A^3} - {B^3} $$ = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)$
C.

${\left( {A + B} \right)^3} $$= {\left( {B + A} \right)^3}$
D.

${\left( {A - B} \right)^3} = {\left( {B - A} \right)^3}$

Câu 5 :

Viết biểu thức ${x^3} + 12{x^2} + 48x + 64$ dưới dạng lập phương của một tổng

A.

${\left( {x + 4} \right)^3}$.
B.

${\left( {x - 4} \right)^3}$.
C.

${\left( {x - 8} \right)^3}$.
D.

${\left( {x + 8} \right)^3}$.

Câu 6 :

Cho $x$ thỏa mãn $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) - x\left( {{x^2} - 2} \right) = 14.$ Chọn câu đúng.

A.

$x = - 3$.
B.

$x = 11$.
C.

$x = 3$.
D.

$x = 4$.

Câu 7 :

Đẳng thức nào sau đây là đúng.

A.

${y^5} - {y^4} = {y^4}\left( {y - 1} \right)$.
B.

${y^5} - {y^4} = {y^3}\left( {{y^2} - 1} \right)$.
C.

${y^5} - {y^4} = {y^5}\left( {1 - y} \right)$.
D.

${y^5} - {y^4} = {y^4}\left( {y + 1} \right)$.

Câu 8 :

Chọn câu đúng.

A.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = - 8\left( {3x + 1} \right)\left( {x + 2} \right)$.
B.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = \left( {3x - 1} \right)\left( {x + 2} \right)$.
C.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = - 8\left( {3x - 1} \right)\left( {x - 2} \right)$.
D.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = - 8\left( {3x - 1} \right)\left( {x + 2} \right)$.

Câu 9 :

Chọn câu đúng.

A.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 2} \right)\left( {x + 2} \right).$
B.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 4} \right).$
C.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 9} \right)\left( {x - 2} \right)\left( {x + 2} \right).$
D.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 2} \right)$.

Câu 10 :

Chia đơn thức ${\left( { - 3x} \right)^5}$ cho đơn thức ${\left( { - 3x} \right)^2}$ ta được kết quả là

A.

$ - 9{x^3}$.
B.

$9{x^3}$.
C.

$27{x^3}$.
D.

$ - 27{x^3}$.

Câu 11 :

Cho $A = {\left( {3{a^2}b} \right)^3}{\left( {a{b^3}} \right)^2}$ ; $B = {\left( {{a^2}b} \right)^4}$ . Khi đó $A:B$ bằng

A.

$27a{b^5}$.
B.

$ - 27{b^5}$.
C.

$27{b^5}$.
D.

$9{b^5}$.

Câu 12 :

Biết phần dư của phép chia đa thức $\left( {{x^5} + {x^3} + {x^2} + 2} \right)$ cho đa thức $\left( {{x^3} + 1} \right)$ là số tự nhiên $a$ . Chọn câu đúng.

A.

$a < 2$.
B.

$a > 1$.
C.

$a < 0$.
D.

$a \vdots 2$.

Câu 13 :

Tìm $a$ và $b$ để đa thức $f\left( x \right) = {x^4} - 9{x^3} + 21{x^2} + ax + b$ chia hết cho đa thức $g\left( x \right) = {x^2} - x - 2$

A.

$a = - 1;\,b = 30$.
B.

$a = 1;\,b = 30$.
C.

$a = - 1;\,b = - 30$.
D.

$a = 1;\,b = - 30$.

Câu 14 :

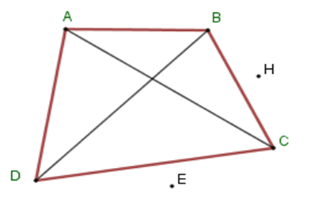
Cho hình vẽ sau. Chọn câu sai.

A.

Hai cạnh kề nhau: $AB,BC$.
B.

Hai cạnh đối nhau: $BC,AD$.
C.

Hai góc đối nhau: $\widehat A$ và $\widehat B$
D.

Các điểm nằm ngoài: $H,E$.

Câu 15 :

Cho hình thang cân $ABCD$ đáy nhỏ $AB = 4cm$ , đáy lớn $CD = 10cm$ , cạnh bên $BC = 5cm$ thì đường cao $AH$ bằng:

A.

$4,5cm\;$
B.

$4cm$
C.

$3,5cm$
D.

$3cm$

Câu 16 :

Hãy chọn câu sai

A.

Độ dài đường trung bình của hình thang bằng nửa tổng hai đáy.
B.

Độ dài đường trung bình của hình thang bằng nửa hiệu hai đáy.
C.

Đường trung bình của hình thang thì song song với hai đáy.
D.

Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.

Câu 17 :

Cho tam giác $ABC$ cân tại $B$ , các đường trung tuyến $AA',BB',CC'$ . Trục đối xứng của tam giác $ABC$ là:

A.

$AA'$
B.

$BB'$
C.

$AA'$ và $CC'$
D.

$CC'$

Câu 18 :

Hãy chọn câu sai:

A.

Điểm đối xứng với điểm $M$ qua $M$ cũng chính là điểm $M$.
B.

Hai điểm $A$ và $B$ gọi là đối xứng với nhau qua điểm $O$ khi $O$ là trung điểm của đoạn thẳng $AB$.
C.

Hình bình hành có một tâm đối xứng.
D.

Đoạn thẳng có hai tâm đối xứng.

Câu 19 :

Tam giác $ABC$ đối xứng với tam giác $A'B'C'$ qua $O$. Biết chu vi của tam giác $A'B'C'$là $32\,cm$. Chu vi của tam giác $ABC$ là :

A.

$32\,dm$.
B.

$64\,cm$.
C.

$16\,cm$.
D.

$32\,cm$.

Câu 20 :

Rút gọn đa thức $16{x^2} - 4x + \dfrac{1}{4}$ ta được kết quả nào sau đây?

A.

${\left( {4x - \dfrac{1}{2}} \right)^2}$
B.

${\left( {x - \dfrac{1}{2}} \right)^2}$
C.

${\left( {4x + \dfrac{1}{2}} \right)^2}$
D.

${\left( {x + \dfrac{1}{2}} \right)^2}$

Câu 21 :

Chọn câu sai.

A.

Giá trị của biểu thức $ax\left( {ax + y} \right)$ tại $x = 1,y = 0$ là ${a^2}$.
B.

Giá trị của biểu thức $a{y^2}(ax + y)$ tại $x = 0,y = 1$ là ${(1 + a)^2}$.
C.

Giá trị của biểu thức $ - xy(x - y)$ tại $x = - 5,y = - 5$ bằng $0$.
D.

Giá trị của biểu thức $xy( - x - y)$ tại $x = 5,y = - 5$ bằng $0$.

Câu 22 :

Phân tích đa thức $mx + my + m$ thành nhân tử ta được

A.

$m\left( {x + y + 1} \right)$.
B.

$m\left( {x + y + m} \right)$.
C.

$m\left( {x + y} \right)$.
D.

$m\left( {x + y - 1} \right)$

Câu 23 :

Chọn câu sai.

A.

${\left( {x - 2} \right)^2} - {\left( {2 - x} \right)^3} = {\left( {x - 2} \right)^2}\left( {x - 1} \right)$.
B.

${\left( {x - 2} \right)^2} - \left( {2 - x} \right) = \left( {x - 2} \right)\left( {x - 1} \right)$.
C.

${\left( {x - 2} \right)^3} - {\left( {2 - x} \right)^2} = {\left( {x - 2} \right)^2}\left( {3 - x} \right)$.
D.

${\left( {x - 2} \right)^2} + x - 2 = \left( {x - 2} \right)\left( {x - 1} \right)$.

Câu 24 :

Tìm một số khác 0 biết rằng bình phương của nó bằng năm lần lập phương của số ấy.

A.

$5$
B.

$\dfrac{1}{5}$
C.

$\dfrac{1}{{25}}$
D.

$ - \dfrac{1}{5}$

Câu 25 :

Cho biết ${x^3} = 2p + 1$ trong đó $x$ là số tự nhiên, $p$ là số nguyên tố. Tìm $x.$

A.

$x = 9$
B.

$x = 7$
C.

$x = 5$
D.

$x = 3$

Câu 26 :

Cho $2x\left( {3x - 1} \right) - 3x\left( {2x - 3} \right) = 11$ .Kết quả $x$ bằng:

A.

$ - \dfrac{{11}}{7}$
B.

$\dfrac{7}{{11}}$
C.

$1$
D.

$\dfrac{{11}}{7}$

Câu 27 :

Rút gọn biểu thức $N = 2{x^n}\left( {3{x^{n + 2}} - 1} \right) - 3{x^{n + 2}}\left( {2{x^n} - 1} \right)$ ta được

A.

$N = 2{x^n} + 3{x^{n + 2}}$
B.

$N = - 2{x^n} - 3{x^{n + 2}}$
C.

$N = - 2{x^n} + 3{x^{n + 2}}$
D.

$N = - 2{x^n} + {x^{n + 2}}$

Câu 28 :

Xác định hệ số $a,b,c$ biết rằng với mọi giá trị của $x$ thì $\left( {ax + 4} \right)\left( {{x^2} + bx - 1} \right) = 9{x^3} + 58{x^2} + 15x + c$

A.

$a = 9,b = - 4,c = 6.$
B.

$a = 9,b = 6,c = - 4.$
C.

$a = 9,b = 6,c = 4.$
D.

$a = - 9,b = - 6,c = - 4.$

Câu 29 :

Rút gọn biểu thức $H = \left( {x + 5} \right)\left( {{x^2} - 5x + 25} \right) - {\left( {2x + 1} \right)^3} + 7{\left( {x - 1} \right)^3} - 3x\left( { - 11x + 5} \right)$ ta được giá trị của $H$ là

A.

Một số lẻ
B.

Một số chẵn
C.

Một số chính phương
D.

Một số chia hết cho $12$

Câu 30 :

Cho ${\left( {a + b + c} \right)^2} + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + bc + ca} \right)$. Khi đó

A.

$a = b = 2c$
B.

$a = b = c$
C.

$a = 2b = c$
D.

$a = b = c = 2$

Câu 31 :

Phân tích đa thức $8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}$ thành nhân tử ta được

A.

${\left( {x + 2y} \right)^3}$.
B.

${\left( {2x + y} \right)^3}$.
C.

${\left( {2x - y} \right)^3}$.
D.

${\left( {8x + y} \right)^3}$.

Câu 32 :

Cho $M = \left( {{x^4}{y^{n + 1}} - \dfrac{1}{2}{x^3}{y^{n + 2}}} \right):\left( {\dfrac{1}{2}{x^3}{y^n}} \right) - 20{x^4}y:5{x^2}y\,\,\,\left( {n \in \mathbb{N};x;y \ne 0} \right)$ . Chọn câu đúng.

A.

Giá trị của $M$ luôn là số âm
B.

Giá trị của $M$ luôn là số dương
C.

Giá trị của $M$ luôn bằng $0$
D.

Giá trị của $M$ luôn bằng $1$

Câu 33 :

Điền vào chỗ trống: $\left( {{x^3} + {x^2} - 12} \right):\left( {x - 2} \right) = .....$

A.

$x + 3$
B.

$x - 3$
C.

${x^2} + 3x + 6$
D.

${x^2} - 3x + 6$

Câu 34 :

$P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}$. Tìm $n \in Z$ để $P \in Z$.

A.

$n \in \left\{ {0,2} \right\}$
B.

$n \in \left\{ { - 1,1} \right\}$
C.

$n \in \left\{ { - 1;2} \right\}$
D.

$n \in \left\{ { - 2,0} \right\}$

Câu 35 :

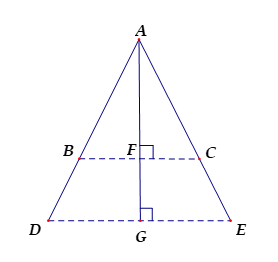
Cho hình vẽ, với $AD = AE,AG$ là trung trực của $DE$. Có bao nhiêu cặp đoạn thẳng đối xứng nhau qua trục $AG$ (các đoạn thẳng thuộc đường thẳng $AD, AE$)? Chọn câu đúng.

A.

$1$
B.

$2$
C.

$3$
D.

$4$

Câu 36 :

Hãy chọn câu đúng?

Cho tam giác $ABC$ có chu vi là $80$. Gọi $E,F,P$ là trung điểm của các cạnh $AB,BC,CA$. Chu vi của tam giác $EFP$ là:

A.

$40\,cm$
B.

$20\,cm$
C.

$45\,cm$
D.

$50\,cm$

Câu 37 :

Cho tam giác $ABC$, đường trung tuyến $AM$. Gọi $D$ là trung điểm của $AM,E$ là giao điểm của $BD$ và $AC,F$ là trung điểm của $EC$. Tính $AE$ biết $AC = 9cm$.

A.

$AE = 4,5\,cm$
B.

$AE = 3\,cm$
C.

$AE = 2\,cm$
D.

$AE = 6\,cm$

Câu 38 :

Tỉ số độ dài hai cạnh của hình bình hành là $3:5$. Còn chu vi của nó bằng $48cm$. Độ dài hai cạnh kề của hình bình hành là:

A.

$12cm$ và $20cm$
B.

$6cm$ và $10cm$
C.

$3cm$ và $5cm$
D.

$9cm$ và $15cm$

Câu 39 :

Cho tam giác $ABC$ có $BC = 6cm.$ Trên cạnh $AB$ lấy các điểm $D$ và $E$ sao cho $AD = BE.$ Qua $D,E$ lần lượt vẽ các đường thẳng song song với $BC,$ cắt $AC$ theo thứ tự ở $G$ và $H$. Tính tổng $DG + EH.$

A.

$10\,cm$
B.

$4\,cm$
C.

$6\,cm$
D.

$8\,cm$

Câu 40 :

Cho tam giác $ABC$ vuông cân tại $A$, $AC = 8\,cm$, điểm $M$ thuộc cạnh $BC$. Gọi $D,E$ theo thứ tự là các chân đường vuông góc kẻ từ $M$ đến $AB,AC$. Chu vi của tứ giác $ADME$ bằng:

A.

$16\,cm$
B.

$38\,cm$
C.

$18\,cm$
D.

$12\,cm$

Lời giải và đáp án

Câu 1 :

Cho hình thang có đáy lớn gấp đôi đáy nhỏ, đáy nhỏ lớn hơn chiều cao $2$ đơn vị. Biểu thức tính diện tích hình thang là:

A.

$S = {3x^2} -6x$
B.

$S = \dfrac{{{3x^2} -6x}}{2}$
C.

$S = \dfrac{{{x^2} + 2x + 4}}{2}$
D.

$S = \dfrac{{{x^2} - 2x - 4}}{2}$

Đáp án : B

Phương pháp giải :

- Gọi $x\,\left( {x > 2} \right)$ là độ dài đáy nhỏ của hình thang

- Biểu diễn chiều cao và đáy lớn hình thang theo $x$

- Sử dụng công thức tính diện tích hình thang: $S = \dfrac{{\left( {a + b} \right).h}}{2}$

Lời giải chi tiết :

Gọi $x\,\left( {x > 2} \right)$ là độ dài đáy nhỏ của hình thang .

Theo giả thiết ta có độ dài đáy lớn là $2x$ , chiều cao của hình thang là $x - 2$

Diện tích hình thang là $S = \dfrac{{\left( {x + 2x} \right)\left( {x - 2} \right)}}{2} = \dfrac{3x(x-2)}{2} = \dfrac{{{3x^2} -6x }}{2}$ (đvdt)

Chú ý

Một số em có thể nhầm công thức diện tích hình thang $S = \left( {a + b} \right)h$ dẫn đến chọn A sai.

Câu 2 :

Khai triển ${\left( {3x - 4y} \right)^2}$ ta được

A.

$9{x^2} - 24xy + 16{y^2}$
B.

$9{x^2} - 12xy + 16{y^2}$
C.

$9{x^2} - 24xy + 4{y^2}$
D.

$9{x^2} - 6xy + 16{y^2}$

Đáp án : A

Phương pháp giải :

Sử dụng công thức bình phương của một hiệu ${\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}$

Lời giải chi tiết :

Ta có ${\left( {3x - 4y} \right)^2} $$= {\left( {3x} \right)^2} - 2.3x.4y + {\left( {4y} \right)^2} $$= 9{x^2} - 24xy + 16{y^2}$

Chú ý

Một số em có thể nhớ nhầm hằng đẳng thức thành ${\left( {A - B} \right)^2} = {A^2} - AB + {B^2}$ từ đó ra đáp án B sai.

Hoặc thực hiện phép bình phương sai ${\left( {4y} \right)^2} = 4{y^2}$ dẫn đến chọn C sai.

Câu 3 :

Rút gọn biểu thức $B = \left( {2a - 3} \right)\left( {a + 1} \right) - {\left( {a - 4} \right)^2} - a\left( {a + 7} \right)$ ta được

A.

$0$
B.

$1$
C.

$19$
D.

$ - 19$

Đáp án : D

Phương pháp giải :

Sử dụng công thức bình phương của một hiệu ${\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}$ và phép nhân đa thức để khai triển và rút gọn.

Lời giải chi tiết :

Ta có $B = \left( {2a - 3} \right)\left( {a + 1} \right) - {\left( {a - 4} \right)^2} - a\left( {a + 7} \right)$$ = 2{a^2} + 2a - 3a - 3 - \left( {{a^2} - 8a + 16} \right) - \left( {{a^2} + 7a} \right)$

$ = 2{a^2} + 2a - 3a - 3 - {a^2} + 8a - 16 - {a^2} - 7a$ $ = - 19$

Chú ý

Một số em có thể nhầm dấu dẫn đến chọn C sai.

Câu 4 :

Chọn câu sai.

A.

${A^3} + {B^3} $$ = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)$
B.

${A^3} - {B^3} $$ = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)$
C.

${\left( {A + B} \right)^3} $$= {\left( {B + A} \right)^3}$
D.

${\left( {A - B} \right)^3} = {\left( {B - A} \right)^3}$

Đáp án : D

Phương pháp giải :

Sử dụng công thức tổng hai lập phương và hiệu hai lập phương

${A^3} + {B^3} $$ = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)$

${A^3} - {B^3}$$ = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)$

Lời giải chi tiết :

Ta có ${A^3} + {B^3} $$ = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)$ và ${A^3} - {B^3}$$ = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)$ nên A, B đúng.

Vì $A + B = B + A $

$ \Rightarrow {\left( {A + B} \right)^3} $$ = {\left( {B + A} \right)^3}$ nên C đúng.

Vì $A - B = - \left( {B - A} \right)$

$ \Rightarrow {\left( {A - B} \right)^3} $$ = - {\left( {B - A} \right)^3}$ nên D sai.

Câu 5 :

Viết biểu thức ${x^3} + 12{x^2} + 48x + 64$ dưới dạng lập phương của một tổng

A.

${\left( {x + 4} \right)^3}$.
B.

${\left( {x - 4} \right)^3}$.
C.

${\left( {x - 8} \right)^3}$.
D.

${\left( {x + 8} \right)^3}$.

Đáp án : A

Phương pháp giải :

Sử dụng công thức lập phương của một tổng ${A^3} + 3{A^2}B + 3A{B^2} + {B^3} = {\left( {A + B} \right)^3}$

Lời giải chi tiết :

Ta có ${x^3} + 12{x^2} + 48x + 64 $$= {x^3} + 3{x^2}.4 + 3.x{.4^2} + {4^3} $$= {\left( {x + 4} \right)^3}$

Chú ý

Một số em có thể sai ở bước phân tích cuối $64 = {8^3}$ dẫn đến chọn đáp án sai.

Câu 6 :

Cho $x$ thỏa mãn $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) - x\left( {{x^2} - 2} \right) = 14.$ Chọn câu đúng.

A.

$x = - 3$.
B.

$x = 11$.
C.

$x = 3$.
D.

$x = 4$.

Đáp án : C

Phương pháp giải :

Sử dụng hằng đẳng thức tổng hai lập phương và phép nhân đa thức để biến đổi về dạng tìm $x$ thường gặp.

Lời giải chi tiết :

Ta có $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) - x\left( {{x^2} - 2} \right) = 15$$ \Leftrightarrow {x^3} + {2^3} - \left( {{x^3} - 2x} \right) = 14 $$\Leftrightarrow {x^3} + 8 - {x^3} + 2x = 14$

$ \Leftrightarrow 2x = 6 \Leftrightarrow x = 3$.

Vậy $x = 3$ .

Chú ý

Một số em có thể sai ở hằng đẳng thức đầu $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) = {x^3} - 8$ nên dẫn đến ra kết quả sai $x = 11$ . Hoặc quên đổi dấu khi phá ngoặc cũng dẫn đến kết quả sai.

Câu 7 :

Đẳng thức nào sau đây là đúng.

A.

${y^5} - {y^4} = {y^4}\left( {y - 1} \right)$.
B.

${y^5} - {y^4} = {y^3}\left( {{y^2} - 1} \right)$.
C.

${y^5} - {y^4} = {y^5}\left( {1 - y} \right)$.
D.

${y^5} - {y^4} = {y^4}\left( {y + 1} \right)$.

Đáp án : A

Lời giải chi tiết :

Ta có ${y^5} - {y^4} = {y^4}.y - {y^4}.1 = {y^4}\left( {y - 1} \right)$

Chú ý

Một số em có thể đặt ${y^5}$ làm nhân tử chung dẫn đến chọn sai đáp án.

Câu 8 :

Chọn câu đúng.

A.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = - 8\left( {3x + 1} \right)\left( {x + 2} \right)$.
B.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = \left( {3x - 1} \right)\left( {x + 2} \right)$.
C.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = - 8\left( {3x - 1} \right)\left( {x - 2} \right)$.
D.

${(5{\rm{x}} - 4)^2} - 49{{\rm{x}}^2} = - 8\left( {3x - 1} \right)\left( {x + 2} \right)$.

Đáp án : D

Phương pháp giải :

Sử dụng hằng đẳng thức ${A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)$ để phân tích đa thức thành nhân tử.

Lời giải chi tiết :

Ta có ${(5x - 4)^2} - 49{x^2} $$= {\left( {5x - 4} \right)^2} - {\left( {7x} \right)^2} $$= \left( {5x - 4 + 7x} \right)\left( {5x - 4 - 7x} \right)$$ = \left( {12x - 4} \right)\left( { - 2x - 4} \right) $$= 4.\left( {3x - 1} \right).\left( { - 2} \right)\left( {x + 2} \right) $$= - 8\left( {3x - 1} \right)\left( {x + 2} \right)$

Chú ý

Một số em có thể sai khi phân tích $\left( { - 2x - 4} \right) = - 2.\left( {x - 2} \right)$ dẫn đến chọn đáp án C sai.

Câu 9 :

Chọn câu đúng.

A.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 2} \right)\left( {x + 2} \right).$
B.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 4} \right).$
C.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 9} \right)\left( {x - 2} \right)\left( {x + 2} \right).$
D.

${x^3} - 4{x^2} - 9x + 36 = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 2} \right)$.

Đáp án : B

Lời giải chi tiết :

Ta có ${x^3} - 4{x^2} - 9x + 36$$ = \left( {{x^3} - 4{x^2}} \right) - \left( {9x - 36} \right) $$ = {x^2}\left( {x - 4} \right) - 9\left( {x - 4} \right) $$ = \left( {{x^2} - 9} \right)\left( {x - 4} \right)$$ = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 4} \right)$

Chú ý

Một số em có thể nhầm dấu khi đưa $36$ vào ngoặc $ - 9x + 36$$ = - \left( {9x + 36} \right)$ dẫn đến không ra được đáp án.

Các em có thể nhóm cách khác ${x^3} - 4{x^2} - 9x + 36 $$ = \left( {{x^3} - 9x} \right) - \left( {4{x^2} - 36} \right) $$ = x\left( {{x^2} - 9} \right) - 4\left( {{x^2} - 9} \right)$

$ = \left( {x - 4} \right)\left( {{x^2} - 9} \right) $$ = \left( {x - 4} \right)\left( {x - 3} \right)\left( {x + 3} \right)$

Câu 10 :

Chia đơn thức ${\left( { - 3x} \right)^5}$ cho đơn thức ${\left( { - 3x} \right)^2}$ ta được kết quả là

A.

$ - 9{x^3}$.
B.

$9{x^3}$.
C.

$27{x^3}$.
D.

$ - 27{x^3}$.

Đáp án : D

Phương pháp giải :

* Sử dụng quy tắc chia đơn thức cho đơn thức.

Muốn chia đơn thức $A$ cho đơn thức $B$ (trong trường hợp $A$ chia hết cho $B$ ) ta làm như sau:

+ Chia hệ số của đơn thức $A$ cho hệ số của đơn thức $B$

+ Chia lũy thừa của từng biến trong $A$ cho lũy thừa của cùng biến đó trong $B$ .

+ Nhân các kết quả vừa tìm được với nhau.

* Sử dụng công thức chia hai lũy thừa cùng cơ số

Lời giải chi tiết :

Ta có ${\left( { - 3x} \right)^5}:{\left( { - 3x} \right)^2} $$= {\left( { - 3x} \right)^3} $$= {\left( { - 3} \right)^3}.{x^3} = - 27{x^3}$.

Chú ý

Một số em có thể nhầm dấu ${\left( { - 3} \right)^3} = 27$ dẫn đến chọn sai đáp án.

Câu 11 :

Cho $A = {\left( {3{a^2}b} \right)^3}{\left( {a{b^3}} \right)^2}$ ; $B = {\left( {{a^2}b} \right)^4}$ . Khi đó $A:B$ bằng

A.

$27a{b^5}$.
B.

$ - 27{b^5}$.
C.

$27{b^5}$.
D.

$9{b^5}$.

Đáp án : C

Phương pháp giải :

+ Rút gọn $A$ . Chú ý công thức ${\left( {{x^m}} \right)^n} = {x^{m.n}}$ .

+ Sử dụng quy tắc chia đơn thức cho đơn thức

Lời giải chi tiết :

Ta có $A = {\left( {3{a^2}b} \right)^3}{\left( {a{b^3}} \right)^2} $$= {3^3}.{\left( {{a^2}} \right)^3}.{b^3}.{a^2}.{\left( {{b^3}} \right)^2} $$= 27{a^6}.{b^3}.{a^2}.{b^6} $$= 27{a^8}{b^9};$ $B = {\left( {{a^2}b} \right)^4} $$= {\left( {{a^2}} \right)^4}.{b^4} $$= {a^8}{b^4}$

Khi đó $A:B = 27{a^8}{b^9}:{a^8}{b^4} $$= 27{b^5}$

Chú ý

Một số em có thể rút gọn nhầm $A$ do tính sai chẳng hạn ${\left( {{a^2}} \right)^3} = {a^5}$ hoặc ${3^3} = 9$ dẫn đến chọn sai đáp án.

Câu 12 :

Biết phần dư của phép chia đa thức $\left( {{x^5} + {x^3} + {x^2} + 2} \right)$ cho đa thức $\left( {{x^3} + 1} \right)$ là số tự nhiên $a$ . Chọn câu đúng.

A.

$a < 2$.
B.

$a > 1$.
C.

$a < 0$.
D.

$a \vdots 2$.

Đáp án : A

Lời giải chi tiết :

Phần dư của phép chia là $a = 1 < 2$

Chú ý

Một số em sai ở phép trừ cuối $\left( {{x^3} + 2} \right) - \left( {{x^3} + 1} \right) = {x^3} + 2 - {x^3} + 1 = 3$ do không đổi dấu khi phá ngoặc nên dẫn đến chọn sai đáp án.

Câu 13 :

Tìm $a$ và $b$ để đa thức $f\left( x \right) = {x^4} - 9{x^3} + 21{x^2} + ax + b$ chia hết cho đa thức $g\left( x \right) = {x^2} - x - 2$

A.

$a = - 1;\,b = 30$.
B.

$a = 1;\,b = 30$.
C.

$a = - 1;\,b = - 30$.
D.

$a = 1;\,b = - 30$.

Đáp án : D

Phương pháp giải :

+ Sử dụng cách chia đa thức một biến đã sắp xếp.

+ Sử dụng nhận xét: Nếu phép chia có phần dư $R = 0$ thì phép chia đó là phép chia hết.

Chú ý: $Ax + B = 0$ với $\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.$ .

Lời giải chi tiết :

Ta có

Phần dư của phép chia $f\left( x \right)$ cho $g\left( x \right)$ là $R = \left( {a - 1} \right)x + b + 30$

Để phép chia trên là phép chia hết thì $R = 0$ với $\forall x$ $ \Leftrightarrow \left( {a - 1} \right)x + b + 30 = 0$ với $\forall x$

$ \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b + 30 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 30\end{array} \right.$ . Vậy $a = 1;\,b = - 30$.

Chú ý

Một số em tính sai ở bước cuối khi thực hiện phép chia dẫn đến phần dư là $R = \left( {a - 1} \right)x + b - 30$ do đó ra sai đáp án.

Câu 14 :

Cho hình vẽ sau. Chọn câu sai.

A.

Hai cạnh kề nhau: $AB,BC$.
B.

Hai cạnh đối nhau: $BC,AD$.
C.

Hai góc đối nhau: $\widehat A$ và $\widehat B$
D.

Các điểm nằm ngoài: $H,E$.

Đáp án : C

Phương pháp giải :

Ta sử dụng kiến thức về các yếu tố góc, đỉnh, cạnh của tứ giác $ABCD$.

Lời giải chi tiết :

Tứ giác $ABCD$ có các cặp góc đối nhau là $\widehat A;\,\widehat C$ và $\widehat B;\,\widehat D$ còn $\widehat A;\,\widehat B$ là hai góc kề nhau nên C sai.

Câu 15 :

Cho hình thang cân $ABCD$ đáy nhỏ $AB = 4cm$ , đáy lớn $CD = 10cm$ , cạnh bên $BC = 5cm$ thì đường cao $AH$ bằng:

A.

$4,5cm\;$
B.

$4cm$
C.

$3,5cm$
D.

$3cm$

Đáp án : B

Phương pháp giải :

Ta sử dụng tính chất hình thang cân và định lý Pytago.

Lời giải chi tiết :

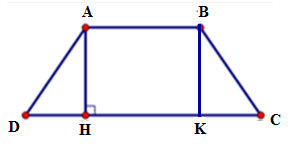
Kẻ $ BK \bot DC$ tại $K.$

Vì $ABCD$ là hình thang cân nên ta có $\widehat D = \widehat C;AD = BC \Rightarrow \Delta AHD = \Delta BKC\left( {ch - gn} \right) \Rightarrow DH = CK$

Suy ra $DH = \dfrac{1}{2}\left( {CD - AB} \right)$

Suy ra $DH = \dfrac{1}{2}\left( {CD - AB} \right) = \dfrac{1}{2}\left( {10 - 4} \right) = 3\,\,cm$

Do $ABCD$ là hình thang cân nên $AD = BC = 5cm$

Áp dụng định lý Py– ta – go vào tam giác $ADH$ vuông tại $H$ ta có $A{D^2} = A{H^2} + D{H^2}$

$ \Rightarrow A{H^2} = A{D^2} - D{H^2} = {5^2} - {3^2} \Rightarrow AH = 4$

Vậy $AH = 4cm$ .

Chú ý

Một số em sử dụng sai định lý Pytago dẫn đến sai đáp án.

Câu 16 :

Hãy chọn câu sai

A.

Độ dài đường trung bình của hình thang bằng nửa tổng hai đáy.
B.

Độ dài đường trung bình của hình thang bằng nửa hiệu hai đáy.
C.

Đường trung bình của hình thang thì song song với hai đáy.
D.

Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.

Đáp án : B

Phương pháp giải :

Ta sử dụng định lý đường trung bình và hình thang

Lời giải chi tiết :

+ Độ dài đường trung bình hình thang bằng nửa tổng hai đáy nên đáp án B sai.

Câu 17 :

Cho tam giác $ABC$ cân tại $B$ , các đường trung tuyến $AA',BB',CC'$ . Trục đối xứng của tam giác $ABC$ là:

A.

$AA'$
B.

$BB'$
C.

$AA'$ và $CC'$
D.

$CC'$

Đáp án : B

Phương pháp giải :

Áp dụng định nghĩa hai điểm đối xứng nhau qua trục: hai điểm $A,A'$ được gọi là đối xứng nhau qua $d$ nếu $d$ là đường trung trực của $AA'$ .

Lời giải chi tiết :

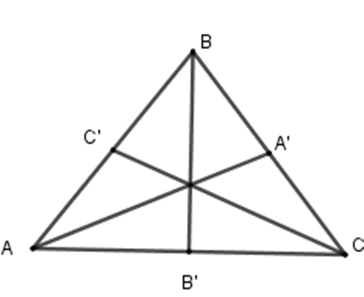
Do tam giác $ABC$ cân tại $B$ , nên đường trung tuyến $BB'$ đồng thời là đường trung trực.

Do đó $BB'$ là trục đối xứng của tam giác $ABC$.

Câu 18 :

Hãy chọn câu sai:

A.

Điểm đối xứng với điểm $M$ qua $M$ cũng chính là điểm $M$.
B.

Hai điểm $A$ và $B$ gọi là đối xứng với nhau qua điểm $O$ khi $O$ là trung điểm của đoạn thẳng $AB$.
C.

Hình bình hành có một tâm đối xứng.
D.

Đoạn thẳng có hai tâm đối xứng.

Đáp án : D

Lời giải chi tiết :

+ Theo định nghĩa hai điểm đối xứng qua một điểm: Hai điểm $A$ , $B$ gọi là đối xứng với nhau qua điểm $O$ nếu $O$ là trung điểm của đoạn thẳng nối hai điểm đó nên B đúng.

+ Trung điểm của đoạn thẳng là tâm đối xứng duy nhất của đoạn thẳng đó nên D sai.

+ Hình bình hành có một tâm đối xứng là giao hai đường chéo, nên C đúng.

+ Điểm đối xứng của một điểm $M$ qua $M$ chính là $M$ nên A đúng.

Câu 19 :

Tam giác $ABC$ đối xứng với tam giác $A'B'C'$ qua $O$. Biết chu vi của tam giác $A'B'C'$là $32\,cm$. Chu vi của tam giác $ABC$ là :

A.

$32\,dm$.
B.

$64\,cm$.
C.

$16\,cm$.
D.

$32\,cm$.

Đáp án : D

Phương pháp giải :

Sử dụng chú ý về hai hình đối xứng với nhau qua một điểm.

“Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.”

Lời giải chi tiết :

Vì tam giác $ABC$ đối xứng với tam giác $A'B'C'$ qua $O$ nên $\Delta ABC = \Delta A'B'C'$ $ \Rightarrow AB = A'B';\,AC = A'C';\,BC = B'C'$

Nên $AB + AC + BC = A'B' + A'C' + B'C'$ $ \Rightarrow {P_{ABC}} = {P_{A'B'C'}}$

Do đó chu vi tam giác $ABC$ là ${P_{ABC}} = 32\,cm$ .

Câu 20 :

Rút gọn đa thức $16{x^2} - 4x + \dfrac{1}{4}$ ta được kết quả nào sau đây?

A.

${\left( {4x - \dfrac{1}{2}} \right)^2}$
B.

${\left( {x - \dfrac{1}{2}} \right)^2}$
C.

${\left( {4x + \dfrac{1}{2}} \right)^2}$
D.

${\left( {x + \dfrac{1}{2}} \right)^2}$

Đáp án : A

Phương pháp giải :

Sử dụng hằng đẳng thức ${\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}$

Lời giải chi tiết :

$16{x^2} - 4x + \dfrac{1}{4} = {\left( {4x} \right)^2} - 2.4x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {\left( {4x - \dfrac{1}{2}} \right)^2}$

Câu 21 :

Chọn câu sai.

A.

Giá trị của biểu thức $ax\left( {ax + y} \right)$ tại $x = 1,y = 0$ là ${a^2}$.
B.

Giá trị của biểu thức $a{y^2}(ax + y)$ tại $x = 0,y = 1$ là ${(1 + a)^2}$.
C.

Giá trị của biểu thức $ - xy(x - y)$ tại $x = - 5,y = - 5$ bằng $0$.
D.

Giá trị của biểu thức $xy( - x - y)$ tại $x = 5,y = - 5$ bằng $0$.

Đáp án : B

Phương pháp giải :

Thay ${x_0};{y_0}$ biểu thức đã cho rồi thực hiện phép tính.

Lời giải chi tiết :

+) Thay $x = 1;\,y = 0$ vào biểu thức $ax\left( {ax + y} \right)$ ta được $a.1\left( {a.1 + 0} \right) = a.a = {a^2}$ nên phương án A đúng

+) Thay $x = 0,y = 1$ vào biểu thức $a{y^2}(ax + y)$ ta được $a{.1^2}\left( {a.0 + 1} \right) = a.1 = a$ nên phương án B sai.

+) Thay $x = - 5,y = - 5$ vào biểu thức $ - xy(x - y)$ ta được $ - \left( { - 5} \right)\left( { - 5} \right)\left[ { - 5 - \left( { - 5} \right)} \right] $$= - 25.0 = 0$ nên phương án C đúng

+) Thay $x = 5,y = - 5$ vào biểu thức $xy( - x - y)$ ta được $5.\left( { - 5} \right)\left[ { - 5 - \left( { - 5} \right)} \right] = - 25.0 = 0$ nên phương án D đúng.

Chú ý

Một số em có thể nhầm dấu khi thay $x,\,y$ vào các biểu thức dẫn đến chọn sai đáp án.

Câu 22 :

Phân tích đa thức $mx + my + m$ thành nhân tử ta được

A.

$m\left( {x + y + 1} \right)$.
B.

$m\left( {x + y + m} \right)$.
C.

$m\left( {x + y} \right)$.
D.

$m\left( {x + y - 1} \right)$

Đáp án : A

Lời giải chi tiết :

Ta có $mx + my + m$$ = m\left( {x + y + 1} \right)$

Câu 23 :

Chọn câu sai.

A.

${\left( {x - 2} \right)^2} - {\left( {2 - x} \right)^3} = {\left( {x - 2} \right)^2}\left( {x - 1} \right)$.
B.

${\left( {x - 2} \right)^2} - \left( {2 - x} \right) = \left( {x - 2} \right)\left( {x - 1} \right)$.
C.

${\left( {x - 2} \right)^3} - {\left( {2 - x} \right)^2} = {\left( {x - 2} \right)^2}\left( {3 - x} \right)$.
D.

${\left( {x - 2} \right)^2} + x - 2 = \left( {x - 2} \right)\left( {x - 1} \right)$.

Đáp án : C

Lời giải chi tiết :

+) Đáp án A: ${\left( {x - 2} \right)^2} - {\left( {2 - x} \right)^3} = {\left( {x - 2} \right)^2} + {\left( {x - 2} \right)^3} = {\left( {x - 2} \right)^2}.\left( {1 + x - 2} \right)$$ = {\left( {x - 2} \right)^2}\left( {x - 1} \right)$ nên A đúng.

+) Đáp án B: ${\left( {x - 2} \right)^2} - \left( {2 - x} \right) = {\left( {x - 2} \right)^2} + \left( {x - 2} \right) = \left( {x - 2} \right)\left( {x - 2 + 1} \right) = \left( {x - 2} \right)\left( {x - 1} \right)$ nên B đúng.

+) Đáp án C: ${\left( {x - 2} \right)^3} - {\left( {2 - x} \right)^2} = {\left( {x - 2} \right)^3} - {\left( {x - 2} \right)^2}$$ = {\left( {x - 2} \right)^2}\left( {x - 2 - 1} \right) = {\left( {x - 2} \right)^2}\left( {x - 3} \right)$ nên C sai.

+) Đáp án D: ${\left( {x - 2} \right)^2} + x - 2 = \left( {x - 2} \right)\left( {x - 2} \right) + \left( {x - 2} \right) = \left( {x - 2} \right)\left( {x - 2 + 1} \right) = \left( {x - 2} \right)\left( {x - 1} \right)$ nên D đúng.

Câu 24 :

Tìm một số khác 0 biết rằng bình phương của nó bằng năm lần lập phương của số ấy.

A.

$5$
B.

$\dfrac{1}{5}$
C.

$\dfrac{1}{{25}}$
D.

$ - \dfrac{1}{5}$

Đáp án : B

Phương pháp giải :

+ Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.

+ Đưa về dạng $A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.$

Lời giải chi tiết :

Gọi số cần tìm là $x\left( {x \ne 0} \right)$. Theo đề bài ta có ${x^2} = 5{x^3} \Leftrightarrow 5{x^3} - {x^2} = 0$$ \Leftrightarrow {x^2}.5x - {x^2} = 0 \Leftrightarrow {x^2}\left( {5x - 1} \right) = 0$

$ \Leftrightarrow \left[ \begin{array}{l}{x^2} = 0\\5x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\left( {loại} \right)\\5x = 1\end{array} \right. \Rightarrow x = \dfrac{1}{5}\left( {tm} \right)$

Vậy số cần tìm là $\dfrac{1}{5}.$

Câu 25 :

Cho biết ${x^3} = 2p + 1$ trong đó $x$ là số tự nhiên, $p$ là số nguyên tố. Tìm $x.$

A.

$x = 9$
B.

$x = 7$
C.

$x = 5$
D.

$x = 3$

Đáp án : D

Phương pháp giải :

+ Chỉ ra $x$ là số lẻ

+ Gọi $x = 2k + 1\,\,\left( {k \in \mathbb{N}} \right)$ sau đó biển đổi để tìm $k$. Từ đó tìm ra $x$

Chú ý rằng: Số nguyên tố là số chỉ có 2 ước là 1 và chính nó.

Lời giải chi tiết :

Vì $p$ là số nguyên tố nên $2p + 1$ là số lẻ. Mà ${x^3} = 2p + 1$ nên ${x^3}$ cũng là một số lẻ, suy ra $x$ là số lẻ

Gọi $x = 2k + 1\,\,\left( {k \in N} \right)$. Ta có ${x^3} = 2p + 1 \Leftrightarrow {\left( {2k + 1} \right)^3} = 2p + 1$

$ \Leftrightarrow 8{k^3} + 12{k^2} + 6k + 1 = 2p + 1 \Leftrightarrow 2p = 8{k^3} + 12{k^2} + 6k$

$ \Leftrightarrow p = 4{k^3} + 6{k^2} + 3k = k\left( {4{k^2} + 6k + 3} \right)$

Mà $p$ là số nguyên tố nên $k = 1 \Rightarrow x = 3$

Vậy số cần tìm là $x = 3.$

Câu 26 :

Cho $2x\left( {3x - 1} \right) - 3x\left( {2x - 3} \right) = 11$ .Kết quả $x$ bằng:

A.

$ - \dfrac{{11}}{7}$
B.

$\dfrac{7}{{11}}$
C.

$1$
D.

$\dfrac{{11}}{7}$

Đáp án : D

Phương pháp giải :

Thực hiện các phép tính: phá ngoặc, chuyển vế .. để biến đổi về dạng tìm $x$ thường gặp

Lời giải chi tiết :

Ta có:

$2x\left( {3x - 1} \right) - 3x\left( {2x - 3} \right) = 11$

$2x.3x - 2x.1 - 3x.2x - 3x.\left( { - 3} \right) = 11$

$6{x^2} - 2x - 6{x^2} + 9x = 11$

$7x = 11$

$x = \dfrac{{11}}{7}$

Vậy $x = \dfrac{{11}}{7}$ .

Câu 27 :

Rút gọn biểu thức $N = 2{x^n}\left( {3{x^{n + 2}} - 1} \right) - 3{x^{n + 2}}\left( {2{x^n} - 1} \right)$ ta được

A.

$N = 2{x^n} + 3{x^{n + 2}}$
B.

$N = - 2{x^n} - 3{x^{n + 2}}$
C.

$N = - 2{x^n} + 3{x^{n + 2}}$
D.

$N = - 2{x^n} + {x^{n + 2}}$

Đáp án : C

Phương pháp giải :

Sử dụng các quy tắc nhân đơn thức với đa thức và sử dụng công thức ${x^m}.{x^n} = {x^{m + n}}$ rồi rút gọn $A$

Lời giải chi tiết :

Ta có $N = 2{x^n}\left( {3{x^{n + 2}} - 1} \right) - 3{x^{n + 2}}\left( {2{x^n} - 1} \right)$

$\begin{array}{l}N = 2{x^n}\left( {3{x^{n + 2}} - 1} \right) - 3{x^{n + 2}}\left( {2{x^n} - 1} \right)\\ = 2{x^n}.3{x^{n + 2}} - 2{x^n}.1 - 3{x^{n + 2}}.2{x^n} - 3{x^{n + 2}}.\left( { - 1} \right)\\ = 6{x^{n + n + 2}} - 2{x^n} - 6.{x^{n + 2 + n}} + 3{x^{n + 2}}\\ = 6{x^{2n + 2}} - 6{x^{2n + 2}} - 2{x^n} + 3{x^{n + 2}}\\ = - 2{x^n} + 3.{x^{n + 2}}\end{array}$

Vậy $N = - 2{x^n} + 3{x^{n + 2}}$

Chú ý

Một số em có thể nhầm dấu của phép tính $ - 3{x^{n + 2}}.\left( { - 1} \right)$ dẫn đến chọn B sai.

Câu 28 :

Xác định hệ số $a,b,c$ biết rằng với mọi giá trị của $x$ thì $\left( {ax + 4} \right)\left( {{x^2} + bx - 1} \right) = 9{x^3} + 58{x^2} + 15x + c$

A.

$a = 9,b = - 4,c = 6.$
B.

$a = 9,b = 6,c = - 4.$
C.

$a = 9,b = 6,c = 4.$
D.

$a = - 9,b = - 6,c = - 4.$

Đáp án : B

Phương pháp giải :

Bước 1: Thực hiện phép nhân đa thức với đa thức

Bước 2: Cho các hệ số của các lũy thừa tương ứng ở hai vế bằng nhau ta tìm được các hệ số $a,b,c.$

Lời giải chi tiết :

Ta có $VT = \left( {ax + 4} \right)\left( {{x^2} + bx - 1} \right)$$ = ax.{x^2} + ax.bx + ax.\left( { - 1} \right) + 4.{x^2} + 4.bx + 4.\left( { - 1} \right)$

$ = a{x^3} + ab{x^2} - ax + 4{x^2} + 4bx - 4$

$ = a{x^3} + \left( {ab{x^2} + 4{x^2}} \right) + \left( {4bx - ax} \right) - 4$

$ = a{x^3} + \left( {ab + 4} \right){x^2} + \left( {4b - a} \right)x - 4$

Theo bài ra ta có $\left( {ax + 4} \right)\left( {{x^2} + bx - 1} \right) = 9{x^3} + 58{x^2} + 15x + c$ đúng với mọi $x$

$ \Leftrightarrow a{x^3} + \left( {ab + 4} \right){x^2} + \left( {4b - a} \right)x - 4 = 9{x^3} + 58{x^2} + 15x + c$ đúng với mọi $x.$

$ \Leftrightarrow \left\{ \begin{array}{l}a = 9\\ab + 4 = 58\\4b - a = 15\\ - 4 = c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 9\\9.b = 54\\4b - 9 = 15\\c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 9\\b = 6\\c = - 4\end{array} \right.$

Vậy $a = 9,b = 6,c = - 4.$

Câu 29 :

A.

Một số lẻ
B.

Một số chẵn
C.

Một số chính phương
D.

Một số chia hết cho $12$

Đáp án : A

Phương pháp giải :

Sử dụng hằng đẳng thức $\left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right) = {A^3} + {B^3}$ , ${\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3},$${\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}$ để phân tích và rút gọn $H$

Lời giải chi tiết :

Ta có $H = \left( {x + 5} \right)\left( {{x^2} - 5x + 25} \right) - {\left( {2x + 1} \right)^3} + 7{\left( {x - 1} \right)^3} - 3x\left( { - 11x + 5} \right)$

$ = {x^3} + {5^3} - \left( {8{x^3} + 3.{{\left( {2x} \right)}^2}.1 + 3.2x{{.1}^2} + 1} \right) + 7\left( {{x^3} - 3{x^2} + 3x - 1} \right) + 33{x^2} - 15x$

$ = {x^3} +125 - 8{x^3} - 12{x^2} - 6x - 1 + 7{x^3} - 21{x^2} + 21x - 7 + 33{x^2} - 15x$

$ = \left( {{x^3} - 8{x^3} + 7{x^3}} \right) + \left( { - 12{x^2} - 21{x^2} + 33{x^2}} \right) + \left( { - 6x + 21x - 15x} \right) +125- 1 - 7$

$ = 117$

Vậy giá trị của $M$ là một số lẻ.

Câu 30 :

Cho ${\left( {a + b + c} \right)^2} + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + bc + ca} \right)$. Khi đó

A.

$a = b = 2c$
B.

$a = b = c$
C.

$a = 2b = c$
D.

$a = b = c = 2$

Đáp án : D

Phương pháp giải :

Biến đổi giả thiết bằng cách sử dụng hằng đẳng thức ${\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)$

${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$

Từ đó đưa về dạng ${A^2} + {B^2} + {C^2} = 0 \Leftrightarrow A = B = C = 0$

Lời giải chi tiết :

Ta có ${\left( {a + b + c} \right)^2} + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + bc + ca} \right)$

$ \Leftrightarrow {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right) + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + ac + bc} \right)$

$ \Leftrightarrow {a^2} + {b^2} + {c^2} - 4a - 4b - 4c + 12 = 0$

$ \Leftrightarrow \left( {{a^2} - 4a + 4} \right) + \left( {{b^2} - 4b + 4} \right) + \left( {{c^2} - 4c + 4} \right) = 0$

$ \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 2} \right)^2} = 0$

Mà ${\left( {a - 2} \right)^2} \ge 0;\,{\left( {b - 2} \right)^2} \ge 0;{\left( {c - 2} \right)^2} \ge 0$ với mọi $a,b,c.$

Nên ${\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 2} \right)^2} \ge 0$ với mọi $a,b,c$

Dấu “=” xảy ra khi $\left\{ \begin{array}{l}a - 2 = 0\\b - 2 = 0\\c - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 2\\c = 2\end{array} \right. \Leftrightarrow a = b = c = 2$

Câu 31 :

Phân tích đa thức $8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}$ thành nhân tử ta được

A.

${\left( {x + 2y} \right)^3}$.
B.

${\left( {2x + y} \right)^3}$.
C.

${\left( {2x - y} \right)^3}$.
D.

${\left( {8x + y} \right)^3}$.

Đáp án : B

Phương pháp giải :

Sử dụng hằng đẳng thức ${\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}$ để phân tích đa thức thành nhân tử.

Lời giải chi tiết :

Ta có $8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}$$ = {\left( {2x} \right)^3} + 3.{\left( {2x} \right)^2}y + 3.2x.{y^2} + {y^3} = {\left( {2x + y} \right)^3}$

Chú ý

Một số em có thể không đưa $8{x^3} = {\left( {2x} \right)^3}$ dẫn đến $8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}$$ = {\left( {8x + y} \right)^3}$và chọn D sai.

Câu 32 :

A.

Giá trị của $M$ luôn là số âm
B.

Giá trị của $M$ luôn là số dương
C.

Giá trị của $M$ luôn bằng $0$
D.

Giá trị của $M$ luôn bằng $1$

Đáp án : A

Phương pháp giải :

+ Sử dụng chia đa thức cho đơn thức $\left( {A + B} \right):C = A:C + B + C$

+ Sử dụng công thức ${a^m}:{a^n} = {a^{m - n}}\,\,\left( {a \ne 0;m \ge n} \right)$

+ Sử dụng đánh giá $ - {A^2} < 0;\,\forall A \ne 0$

Lời giải chi tiết :

Ta có $M = \left( {{x^4}{y^{n + 1}} - \dfrac{1}{2}{x^3}{y^{n + 2}}} \right):\left( {\dfrac{1}{2}{x^3}{y^n}} \right) - 20{x^4}y:\left( {5{x^2}y} \right)\,\,$

$ = \left( {{x^4}{y^{n + 1}}} \right):\left( {\dfrac{1}{2}{x^3}{y^n}} \right) - \left( {\dfrac{1}{2}{x^3}{y^{n + 2}}} \right):\left( {\dfrac{1}{2}{x^3}{y^n}} \right) - 4{x^2}$

$ = 2{x^{4 - 1}}{y^{n + 1 - n}} - {x^{3 - 3}}{y^{n + 2 - n}} - 4{x^2}$

$ = 2xy - {y^2} - 4{x^2}$$ = - \left( {{y^2} - 2xy + {x^2} + 3{x^2}} \right) = - \left[ {{{\left( {x - y} \right)}^2} + 3{x^2}} \right]$

Vì với $x,y \ne 0$ thì ${\left( {x - y} \right)^2} + 3{x^2} > 0$ nên $ - \left[ {{{\left( {x - y} \right)}^2} + 3{x^2}} \right] < 0;\,\forall x;y \ne 0$

Hay giá trị của $M$ luôn là số âm.

Câu 33 :

Điền vào chỗ trống: $\left( {{x^3} + {x^2} - 12} \right):\left( {x - 2} \right) = .....$

A.

$x + 3$
B.

$x - 3$
C.

${x^2} + 3x + 6$
D.

${x^2} - 3x + 6$

Đáp án : C

Phương pháp giải :

- Đặt phép chia.

- Chia hạng tử bậc cao nhất của đa thức bị chia cho hạng tử bậc cao nhất của đa thức chia.

- Nhân kết quả tìm được với đa thức chia, rồi lấy đa thức bị chia trừ đi tích nhận được, hiệu tìm được gọi là dư thứ nhất.

- Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức chia, được kết quả lại thực hiện tương tự như trên, cho đến khi dư cuối cùng không thể chia được nữa.

- Ta thu được thương cần tìm trong ô trống.

Lời giải chi tiết :

Vậy đa thức cần điền vào chỗ trống là ${x^2} + 3x + 6$.

Câu 34 :

$P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}$. Tìm $n \in Z$ để $P \in Z$.

A.

$n \in \left\{ {0,2} \right\}$
B.

$n \in \left\{ { - 1,1} \right\}$
C.

$n \in \left\{ { - 1;2} \right\}$
D.

$n \in \left\{ { - 2,0} \right\}$

Đáp án : A

Phương pháp giải :

- Đặt phép chia.

- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia. Suy ra, số chia là ước của số dư cuối cùng.

- Lập bảng thử chọn để chọn ra giá trị của $n$thỏa mãn.

Lời giải chi tiết :

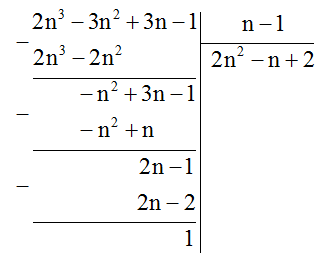
$2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1$

Để $2{n^3} - 3{n^2} + 3n - 1$ chia hết cho $n - 1$ thì $1$ chia hết cho $n - 1$.

$ \Rightarrow \left( {n - 1} \right) \in \left\{ {1, - 1} \right\}$

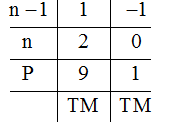
Vậy $n \in \left\{ {0,2} \right\}$ để $P \in Z$.

Câu 35 :

A.

$1$
B.

$2$
C.

$3$
D.

$4$

Đáp án : C

Phương pháp giải :

Bước 1: Ta sử dụng định nghĩa: “Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó” để tìm các cặp điểm đối xứng nhau qua đường thẳng $m$.

Bước 2: Từ đó suy ra các đoạn thẳng đối xứng nhau qua đường thẳng $m$.

Lời giải chi tiết :

Từ giả thiết ta thấy $\Delta ADE$ cân tại $A$ có $AG$ là đường cao nên $AG$ cũng là đường trung trực của $DE.$

Nên điểm $D$ và $E$ đối xứng với nhau qua $AG$.

Lại có $BC//DE$ (cùng vuông với $AG$) nên suy ra $\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}}$ (định lý Ta-lét)

Mà $AD = AE\left( {gt} \right) \Rightarrow AB = AC$. Do đó $\Delta ABC$ cân tại $A$ có $AF$ là đường cao nên $AF$ cũng là đường trung trực của $BC$.

Từ đó điểm $B,C$ đối xứng nhau qua $AG$.

Như vậy:

+ Hai đoạn thẳng $BD,CE$ đối xứng nhau qua $AG$

+ Hai đoạn thẳng $AB,AC$ đối xứng nhau qua $AG$

+ Hai đoạn thẳng $AD,AE$ đối xứng nhau qua $AG$

Chú ý

Các em có thể suy trực tiếp ra các đoạn thẳng đối xứng mà không cần thông qua điểm.

Câu 36 :

Hãy chọn câu đúng?

Cho tam giác $ABC$ có chu vi là $80$. Gọi $E,F,P$ là trung điểm của các cạnh $AB,BC,CA$. Chu vi của tam giác $EFP$ là:

A.

$40\,cm$
B.

$20\,cm$
C.

$45\,cm$
D.

$50\,cm$

Đáp án : A

Phương pháp giải :

Ta sử dụng định lý đường trung bình của tam giác để tìm mối liên hệ giữa chu vi tam giác $ABC$ và chu vi tam giác $EFP$.

Lời giải chi tiết :

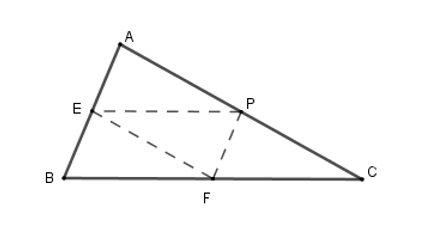
Vì $E,F,P$ là trung điểm của các cạnh $AB,BC,CA$ nên $EF;EP;FP$ là các đường trung bình của tam giác $ABC$.

Suy ra $EF = \dfrac{1}{2}AC;\,FP = \dfrac{1}{2}AB;\,EP = \dfrac{1}{2}BC$ $ \Rightarrow EF + FP + EP = \dfrac{1}{2}AC + \dfrac{1}{2}AB + \dfrac{1}{2}BC$

$ \Leftrightarrow EF + FP + EP = \dfrac{1}{2}\left( {AB + AC + BC} \right)$ hay chu vi tam giác $EFP = \dfrac{1}{2}$ chu vi tam giác $ABC$.

Do đó chu vi tam giác $EFP$ là $80:2 = 40$.

Câu 37 :

A.

$AE = 4,5\,cm$
B.

$AE = 3\,cm$
C.

$AE = 2\,cm$
D.

$AE = 6\,cm$

Đáp án : B

Phương pháp giải :

Bước 1: Sử dụng các dấu hiệu nhận biết đường trung bình để chứng minh các đoạn thẳng là đường trung bình của tam giác.

Bước 2: Từ đó rút ra các mối liện hệ giữa các đoạn thẳng.

Lời giải chi tiết :

Xét tam giác $BEM$ có $BM = MC,EF = FC$ nên $MF$ là đường trung bình của tam giác $BEC$. Do đó $MF{\rm{//}}BE$.

Xét tam giác $AMF$ có $AD = DM,DE//MF$ nên $DE$ là đường trung bình của tam giác $AMF$. Do đó $AE = EF$.

Do đó $AE = EF = FC$ nên $AE = \dfrac{1}{3}AC = \dfrac{1}{3}. 9 = 3cm$.

Câu 38 :

Tỉ số độ dài hai cạnh của hình bình hành là $3:5$. Còn chu vi của nó bằng $48cm$. Độ dài hai cạnh kề của hình bình hành là:

A.

$12cm$ và $20cm$
B.

$6cm$ và $10cm$
C.

$3cm$ và $5cm$
D.

$9cm$ và $15cm$

Đáp án : D

Phương pháp giải :

Gọi độ dài hai cạnh của hình bình hành là $a$ và $b$ rồi áp dụng tính chất dãy tỉ số bằng nhau để tìm $a,b$.

Lưu ý: Tổng của $a,b$ là nửa chu vi hình bình hành.

Lời giải chi tiết :

Gọi độ dài hai cạnh của hình bình hành là $a$ và $b$ với $a,b > 0.$

Theo bài ra ta có: $\dfrac{a}{3} = \dfrac{b}{5}$.

Nửa chu vi của hình bình hành là: $48:2 = 24cm$.

Suy ra: $a+b=24cm.$ Theo tính chất của dãy tỉ số bằng nhau ta có:

$\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{{a + b}}{{3 + 5}} = \dfrac{{24}}{8} = 3\\ \Rightarrow a = 3. 3 = 9\\b = 3. 5 = 15\end{array}$.

Vậy hai cạnh của hình bình hành là $9cm$ và $15cm$.

Câu 39 :

A.

$10\,cm$
B.

$4\,cm$
C.

$6\,cm$
D.

$8\,cm$

Đáp án : C

Phương pháp giải :

+ Kẻ $HM//AB\,\,\left( {M \in BC} \right)$.

+ Chứng minh $DG = MC$ từ hai tam giác bằng nhau từ đó tính tổng $DG + EH$.

Lời giải chi tiết :

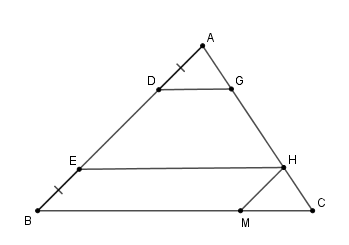
Kẻ $HM//AB\,\,\left( {M \in BC} \right)$.

Xét tứ giác $EHMB$ có $MH//EB;EH//BM$ nên $EHMB$ là hình bình hành.

Suy ra $EH = BM;\,EB = HM$ (tính chất hình bình hành) mà $AD = BE \Rightarrow AD = MH$.

Lại có: $DG//BC \Rightarrow \widehat {ADG} = \widehat {ABC}$ (hai góc ở vị trí đồng vị) (1)

Và $HM//AB \Rightarrow \widehat {HMC} = \widehat {ABC}$ và $\widehat {CHM} = \widehat {CAB}$ (hai góc ở vị trí đồng vị) (2)

Từ (1) và (2) suy ra: $\widehat {HMC} = \widehat {ADG}\left( { = \widehat {ABC}} \right)$.

Xét $\Delta ADG$ và $\Delta HMC$ có: $\left\{ \begin{array}{l}\widehat {MHC} = \widehat {DAG}\left( {cmt} \right)\\AD = HM\,\left( {cmt} \right)\\\widehat {HMC} = \widehat {ADG}\left( {cmt} \right)\end{array} \right.$ nên $\Delta ADG = \Delta HMC\left( {g - c - g} \right) \Rightarrow DG = MC$.

Ta có: $DG + EH = MC + BM = BC = 6cm$.

Câu 40 :

A.

$16\,cm$
B.

$38\,cm$
C.

$18\,cm$
D.

$12\,cm$

Đáp án : A

Phương pháp giải :

Bước 1: Trước hết ta chứng minh $ADME$ là hình chữ nhật dựa vào dấu hiệu tứ giác có $3$ góc vuông là hình chữ nhật.

Bước 2: Chứng minh tam giác $BDM$ vuông cân tại $D$ để suy ra $BD = DM$.

Bước 3: Tính chu vi $ADME$ thông độ dài cạnh tam giác vuông cân.

Lời giải chi tiết :

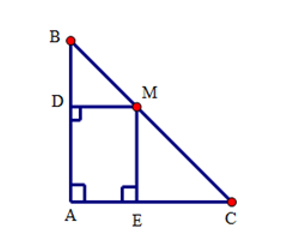
+ Xét tứ giác $ADME$ có $\widehat A = \widehat E = \widehat D = {90^ \circ }$ nên $ADME$ là hình chữ nhật.

+ Xét tam giác $DMB$ có $\widehat B = {45^ \circ }$(do tam giác $ABC$ vuông cân) nên tam giác $BDM$ vuông cân tại $D$. Do đó $DM = BD$.

+ Do $ADME$ là hình chữ nhật nên chu vi $ADME$ là:

$\left( {AD + DM} \right). 2 = \left( {AD + BD} \right). 2 = 8. 2 = 16\left( {cm} \right)$.

Vậy chu vi $ADME$ là $16\,cm$.

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link

Các bài khác cùng chuyên mục

Bài giải mới nhất

Đề kiểm tra giữa học kì 1 Toán 8 - Đề số 3

Báo lỗi góp ý