Bài tập trắc nghiệm Toán 4 - chân trời sáng tạo có đáp án Bài tập trắc nghiệm Chủ đề 4 Phân số

Trắc nghiệm Bài 78: Ôn tập hình học và đo lường Toán 4 Chân trời sáng tạo

Đề bài

Câu 1 :

\(6\) tấn \( = \,...\,kg\).

Số thích hợp điền vào chỗ chấm là:

A. \(60000\)

B. \(6000\)

C. \(600\)

D. \(60\)

Câu 2 :

Điền số thích hợp vào ô trống: 

\(15\) thế kỉ \( = \) 

năm.

Câu 3 :

\(3\) phút \(15\) giây = … giây.

Số thích hợp điền vào chỗ chấm là:

A. \(315\)

B. \(215\)

C. \(195\)

D. \(45\)

Câu 4 :

Điền số thích hợp vào ô trống:

\(900c{m^2} = \) 

\(d{m^2}\).

Câu 5 :

\(7{m^2}\,\,86c{m^2}\, = \,...\,c{m^2}\).

Số thích hợp điền vào chỗ chấm là:

A. \(786\)

B. \(7086\)

C. \(78600\)

D. \(70086\)

Câu 6 :


Chọn dấu thích hợp để điền vào chỗ chấm:

\(\dfrac{2}{5}{m^2}\,\,\,...\,\,\,2250c{m^2}\)

A. \( > \)

B. \( < \)

C. \( = \)

Câu 7 :

Một cuộc thi chạy \(400m\) có ba bạn tham gia là Hà, Nam và Bình. Hà chạy mất \(\dfrac{1}{{10}}\) giờ, Nam chạy mất \(315\) giây, Bình chạy hết \(5\) phút \(5\) giây. Hỏi bạn nào chạy nhanh nhất?

A. Bạn Hà

B. Bạn Nam

C. Bạn Bình   

Câu 8 :

Một khu rừng hình chữ nhật có chiều dài \(6km\), chiều rộng là \(3500m\). Hỏi diện tích khu vườn đó bằng bao nhiêu ki-lô-mét vuông?

A. \(21k{m^2}\)

B. \(210k{m^2}\)

C. \(2100k{m^2}\)

D. \(21\,\,000k{m^2}\)

Câu 9 :

Điền số thích hợp vào ô trống:

Một mảnh vườn hình chữ nhật có chiều rộng 9m, chiều dài gấp ba lần chiều rộng. Người ta trồng rau trên mảnh vườn đó, cứ \(1{m^2}\) thu được \(5kg\) rau.


Vậy trên mảnh vườn đó người ta thu hoạch được

kg rau

Câu 10 :

Một xe tải bé chở \(18\) bao gạo, mỗi bao nặng \(50kg\). Một xe tải lớn chở \(40\) bao gạo, mỗi bao nặng \(75kg\). Hỏi xe tải lớn chở nhiều hơn xe tải xe bao nhiêu tạ gạo?

A. \(2100\) tạ  

B. \(3900\) tạ

C. \(21\) tạ

D. \(39\) tạ

Câu 11 :


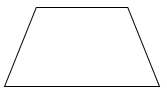
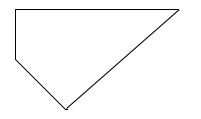
Trong các hình sau, hình nào là hình bình hành?

A.

         

B.

          

C.

          

D.

          

Câu 12 :

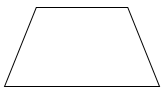
Trong các hình sau, hình nào là hình thoi?

A.

          

B.

          

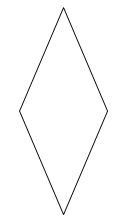
C.

           

D.

          

Câu 13 :

Điền số thích hợp vào ô trống:

Hình chữ nhật MNPQ có 

cặp cạnh vuông góc với nhau.

Câu 14 :

Để lát nền một phòng học hình chữ nhật người ta dùng loại gạch men hình vuông có cạnh \(30cm\). Hỏi cần bao nhiêu viên gạch để lát kín nền phòng học đó, biết rằng nền phòng học có chiều rộng \(6m\) và chiều dài \(12m\) và phần mạch vữa không đáng kể?

A. \(750\) viên gạch   

B. \(800\) viên gạch

C. \(900\) viên gạch

D. \(1000\) viên gạch

Câu 15 :

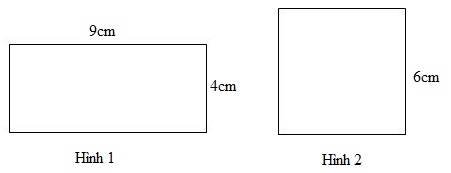
Cho hình chữ nhật và hình vuông có kích thước như hình vẽ:

a) Chu vi hình \(1\) bằng chu vi hình \(2\).

Đúng
Sai

b) Diện tích hình \(1\) bằng diện tích hình \(2\).

Đúng
Sai

c) Diện tích hình \(2\) lớn hơn diện tích hình \(1\).

Đúng
Sai

d) Chu vi hình \(1\) lớn hơn chu vi hình \(2\).

Đúng
Sai
Câu 16 :

Tính diện tích mảnh đất có kích thước như hình vẽ như bên dưới:

A. \(280{m^2}\)

B. \(336{m^2}\)

C. \(448{m^2}\)

D. \(560{m^2}\)

Lời giải và đáp án

Câu 1 :

\(6\) tấn \( = \,...\,kg\).

Số thích hợp điền vào chỗ chấm là:

A. \(60000\)

B. \(6000\)

C. \(600\)

D. \(60\)

Đáp án

B. \(6000\)

Phương pháp giải :

Dựa vào bảng đơn vị đo khối lượng : $1$ tấn $ = {\rm{ }}1000kg$.

Lời giải chi tiết :

Ta có: $1$ tấn $ = {\rm{ }}1000kg$ nên \(6\) tấn $ = 1000kg\,\times \,6\, = \,6000kg$.

Vậy số thích hợp điền vào chỗ chấm là \(6000\).

Câu 2 :

Điền số thích hợp vào ô trống: 

\(15\) thế kỉ \( = \) 

năm.

Đáp án

\(15\) thế kỉ \( = \) 

năm.

Phương pháp giải :

Ta có \(1\) thế kỉ \( = \,\,100\) năm, do đó để đổi đổi một số từ đơn vị thế kỉ sang đơn vị năm ta lấy số đó nhân với \(100\).

Lời giải chi tiết :

Ta có \(1\) thế kỉ \( = \,\,100\) năm, do đó \(15\) thế kỉ \( = 100\) năm \( \times \,\,15\,\, = \,\,1500\) năm.

Vậy đáp án đúng điền vào ô trống là \(1500\).

Câu 3 :

\(3\) phút \(15\) giây = … giây.

Số thích hợp điền vào chỗ chấm là:

A. \(315\)

B. \(215\)

C. \(195\)

D. \(45\)

Đáp án

C. \(195\)

Phương pháp giải :

 Sử dụng cách đổi \(1\) phút \( = \,60\) giây để đổi \(3\) phút sang đơn vị đo là giây rồi cộng thêm với \(15\) giây.

Lời giải chi tiết :

Ta có \(1\) phút \( = \,60\) giây nên \(3\) phút \( = \,\,180\) giây.

\(3\) phút \(15\) giây \(=\,3\) phút \(+\,15\) giây \( = \,180\) giây \(+\,15\) giây \( = \,195\) giây.

Vậy số thích hợp điền vào chỗ chấm là \(195\).

Câu 4 :

Điền số thích hợp vào ô trống:

\(900c{m^2} = \) 

\(d{m^2}\).

Đáp án

\(900c{m^2} = \) 

\(d{m^2}\).

Phương pháp giải :

Áp dụng cách đổi:  \(1d{m^2} = 100c{m^2}\).

Lời giải chi tiết :

Ta có: \(1d{m^2} = 100c{m^2}\)

Nhẩm: \(900:100 = 9\).

Do đó ta có: \(900c{m^2} = 9\,\,d{m^2}\)

Vậy đáp án đúng điền vào ô trống là \(9\).

Câu 5 :

\(7{m^2}\,\,86c{m^2}\, = \,...\,c{m^2}\).

Số thích hợp điền vào chỗ chấm là:

A. \(786\)

B. \(7086\)

C. \(78600\)

D. \(70086\)

Đáp án

D. \(70086\)

Phương pháp giải :

Áp dụng tính chất: \(1{m^2} = 10000c{m^2}\) để đổi đổi \(7{m^2}\) sang đơn vị \(c{m^2}\), sau đó cộng thêm với \(86c{m^2}\).

Lời giải chi tiết :

Ta có \(1{m^2} = 10000c{m^2}\) nên \(7{m^2} = 70000c{m^2}\)

\(7{m^2}\,\,86c{m^2} = \,7{m^2} + 86c{m^2} = 70000c{m^2} + 86c{m^2} = 70086c{m^2}\)

Vậy \(7{m^2}\,\,86c{m^2}\, = \,70086\,c{m^2}\).

Câu 6 :


Chọn dấu thích hợp để điền vào chỗ chấm:

\(\dfrac{2}{5}{m^2}\,\,\,...\,\,\,2250c{m^2}\)

A. \( > \)

B. \( < \)

C. \( = \)

Đáp án

A. \( > \)

Phương pháp giải :

- Đổi $1{m^2}$ sang đơn vị $c{m^2}$.

  Muốn tìm \(\dfrac{2}{5}\) của một số ta lấy số đó chia cho \(5\) rồi nhân với \(2\) hoặc lấy số đó nhân với \(\dfrac{2}{5}.\)

- So sánh kết quả ở hai vế rồi rút ra kết luận.

Lời giải chi tiết :

Ta có: \(1{m^2} = 10000c{m^2}\)

Nên \(\dfrac{2}{5}{m^2}\,= \,10000c{m^2} \times \dfrac{2}{5} = 4000c{m^2}\)

Mà \(4000c{m^2} > 2250c{m^2}\).

Do đó \(\dfrac{2}{5}{m^2}\,> \,2250c{m^2}\).

Vậy dấu thích hợp điền vào chỗ chấm là \(>\).

Câu 7 :

Một cuộc thi chạy \(400m\) có ba bạn tham gia là Hà, Nam và Bình. Hà chạy mất \(\dfrac{1}{{10}}\) giờ, Nam chạy mất \(315\) giây, Bình chạy hết \(5\) phút \(5\) giây. Hỏi bạn nào chạy nhanh nhất?

A. Bạn Hà

B. Bạn Nam

C. Bạn Bình   

Đáp án

C. Bạn Bình   

Phương pháp giải :

- Đổi các đơn vị thời gian về cùng một đơn vị đo là giây, lưu ý \(1\) phút \(=\,60\) giây.

- So sánh thời gian các bạn đã chạy, thời gian của ai ít nhất thì người đó chạy nhanh nhất.

Lời giải chi tiết :

Ta có:

\(\dfrac{1}{{10}}\) giờ  $ = 60$ phút \(:\,1\,0\, = \,6\) phút \( = 360\) giây

\(5\) phút \(5\) giây \( = 5\,\) phút \( + \,\,5\) giây \( = 300\) giây \( + \,\,5\) giây \( = 305\) giây

Ta thấy:  \(305\) giây  $ < {\rm{ 315}}$ giây  $ < {\rm{ 360}}$ giây

Hay \(5\) phút \(5\) giây \( < \,315\) giây \( < \,\dfrac{1}{{10}}\) giờ

Vậy bạn Bình chạy nhanh nhất.

Câu 8 :

Một khu rừng hình chữ nhật có chiều dài \(6km\), chiều rộng là \(3500m\). Hỏi diện tích khu vườn đó bằng bao nhiêu ki-lô-mét vuông?

A. \(21k{m^2}\)

B. \(210k{m^2}\)

C. \(2100k{m^2}\)

D. \(21\,\,000k{m^2}\)

Đáp án

A. \(21k{m^2}\)

Phương pháp giải :

- Đổi \(6km\) sang đơn vị đo là \(m\).

- Tính diện tích hình chữ nhật theo công thức:

            Diện tích = chiều dài × chiều rộng

- Đổi số đo diện tích vừa tìm được sang đơn vị đo là ki-lô-mét vuông.

Lời giải chi tiết :

Đổi $6km = 6000m$

Diện tích khu rừng hình chữ nhật đó là:

            \(\begin{array}{l}6000 \times 3500 = 21\,\,000\,\,000\,({m^2})\\21\,\,000\,\,000\,{m^2}\,\, = \,\,21k{m^2}\end{array}\)

                                                Đáp số: \(21k{m^2}\).

Câu 9 :

Điền số thích hợp vào ô trống:

Một mảnh vườn hình chữ nhật có chiều rộng 9m, chiều dài gấp ba lần chiều rộng. Người ta trồng rau trên mảnh vườn đó, cứ \(1{m^2}\) thu được \(5kg\) rau.


Vậy trên mảnh vườn đó người ta thu hoạch được

kg rau

Đáp án

Một mảnh vườn hình chữ nhật có chiều rộng 9m, chiều dài gấp ba lần chiều rộng. Người ta trồng rau trên mảnh vườn đó, cứ \(1{m^2}\) thu được \(5kg\) rau.


Vậy trên mảnh vườn đó người ta thu hoạch được

kg rau

Phương pháp giải :

- Tính chiều dài ta lấy chiều rộng nhân với \(3\).

- Tính diện tích mảnh vườn ta lấy chiều dài nhân với chiều rộng.

- Tính số kg rau thu được trên cả mảnh vườn ta lấy số kg rau thu được trên \(1{m^2}\) đất nhân với diện tích mảnh vườn.

- Đổi số đo vừa tìm được sang đơn vị tạ.

Lời giải chi tiết :

Chiều dài mảnh vườn đó là:

         9 x 3 = 27 (m)  

Diện tích mảnh vườn đó là:

         27 x 9 = 243 (m2)

Trên mảnh vườn đó người ta thu hoạch được số kg rau là:

       243 x 5 = 1215 (kg)

              Đáp số: 1215 kg rau

Vậy đáp án đúng điền vào ô trống là 1215

 

Câu 10 :

Một xe tải bé chở \(18\) bao gạo, mỗi bao nặng \(50kg\). Một xe tải lớn chở \(40\) bao gạo, mỗi bao nặng \(75kg\). Hỏi xe tải lớn chở nhiều hơn xe tải xe bao nhiêu tạ gạo?

A. \(2100\) tạ  

B. \(3900\) tạ

C. \(21\) tạ

D. \(39\) tạ

Đáp án

C. \(21\) tạ

Phương pháp giải :

- Tìm số gạo xe tải bé chở được ta lấy khối lượng \(1\) bao gạo xe tải bé chở nhân với số bao.

- Tìm số gạo xe tải lớn chở được ta lấy khối lượng \(1\) bao gạo xe tải lớn chở nhân với số bao.

- Tìm hiệu giữa số gạo xe tải lớn chở và số gạo xe tải bé chở.

- Áp dụng cách đổi \(1\) tạ \( = 100kg\) để đổi số đo vừa tìm được sang đơn vị là tạ,

Lời giải chi tiết :

Xe tải bé chở được số ki-lô-gam gạo là:

             \(50 \times 18 = 900\,\,(kg)\)

Xe tải lớn chở được số ki-lô-gam gạo là:

            \(75 \times 40 = 3000\,\,(kg)\)

 Xe tải lớn chở nhiều hơn xe tải xe số gạo là:

             \(3000\, - 900 = 2100\,\,(kg)\)

             \(2100kg = 21\) tạ

                                      Đáp số: \(21\) tạ.

Câu 11 :


Trong các hình sau, hình nào là hình bình hành?

A.

         

B.

          

C.

          

D.

          

Đáp án

C.

          

Phương pháp giải :

Quan sát các hình vẽ và áp dụng tính chất: hình bình hành có hai cặp cạnh đối diện song song và bằng nhau.

Lời giải chi tiết :

Quan sát các hình đã cho ta thấy hình A là hình tròn; hình B là hình thang, hình D là tứ giác ; hình C có hai cặp cạnh đối diện song song và bằng nhau nên hình C là hình bình hành.

Vậy trong các hình đã cho, hình C là hình bình hành.

Câu 12 :

Trong các hình sau, hình nào là hình thoi?

A.

          

B.

          

C.

           

D.

          

Đáp án

B.

          

Phương pháp giải :

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

Lời giải chi tiết :

Quan sát các hình đã cho ta thấy hình A là hình thang, hình B là hình thoi, hình C là hình tròn, hình D là hình bình hành.

Vậy trong các hình đã cho, hình B là hình thoi.

Câu 13 :

Điền số thích hợp vào ô trống:

Hình chữ nhật MNPQ có 

cặp cạnh vuông góc với nhau.

Đáp án

Hình chữ nhật MNPQ có 

cặp cạnh vuông góc với nhau.

Phương pháp giải :

Quan sát hình vẽ để xác định các cặp cạnh vuông góc với nhau.

Lời giải chi tiết :

Trong hình chữ nhật MNPQ có: 

MN vuông góc với MQ;         MN vuông góc với NP;

PQ vuông góc với PN;            PQ vuông góc với QM.

Vậy hình chữ nhật MNPQ có \(4\) cặp cạnh vuông góc với nhau.

Đáp án đúng điền vào ô trống là \(4\).

Câu 14 :

Để lát nền một phòng học hình chữ nhật người ta dùng loại gạch men hình vuông có cạnh \(30cm\). Hỏi cần bao nhiêu viên gạch để lát kín nền phòng học đó, biết rằng nền phòng học có chiều rộng \(6m\) và chiều dài \(12m\) và phần mạch vữa không đáng kể?

A. \(750\) viên gạch   

B. \(800\) viên gạch

C. \(900\) viên gạch

D. \(1000\) viên gạch

Đáp án

B. \(800\) viên gạch

Phương pháp giải :

- Tính diện tích một viên gạch theo công thức tính diện tích hình vuông:

                        Diện tích = cạnh × cạnh

- Tính diện tích căn phòng ta lấy chiều dài nhân với chiều rộng, sau đó đổi số đo vừa tìm được sang đơn vị đo là \(c{m^2}\).

 - Để tìm số viên gạch cần dùng ta lấy diện tích căn phòng (với đơn vị đo là \(c{m^2}\)) chia cho diện tích một viên gạch.

Lời giải chi tiết :

Diện tích một viên gạch là:

            \(30 \times 30 = 900\,\,(c{m^2})\)

Diện tích căn phòng đó là:

            \(\begin{array}{l}12 \times 6 = 72\,\,({m^2})\\72{m^2} = 720000c{m^2}\end{array}\)

Để lát kín nền căn phòng đó người ta cần dùng số viên gạch là:

            \(720000:900 = 800\) (viên gạch)

                                   Đáp số: \(800\) viên gạch.

Câu 15 :

Cho hình chữ nhật và hình vuông có kích thước như hình vẽ:

a) Chu vi hình \(1\) bằng chu vi hình \(2\).

Đúng
Sai

b) Diện tích hình \(1\) bằng diện tích hình \(2\).

Đúng
Sai

c) Diện tích hình \(2\) lớn hơn diện tích hình \(1\).

Đúng
Sai

d) Chu vi hình \(1\) lớn hơn chu vi hình \(2\).

Đúng
Sai
Đáp án

a) Chu vi hình \(1\) bằng chu vi hình \(2\).

Đúng
Sai

b) Diện tích hình \(1\) bằng diện tích hình \(2\).

Đúng
Sai

c) Diện tích hình \(2\) lớn hơn diện tích hình \(1\).

Đúng
Sai

d) Chu vi hình \(1\) lớn hơn chu vi hình \(2\).

Đúng
Sai
Phương pháp giải :

Áp dụng các công thức:

- Chu vi hình vuông = cạnh \( \times \,4\).           

- Diện tích hình vuông = cạnh \( \times \) cạnh.

- Chu vi hình chữ nhật = (chiều dài + chiều rộng) \( \times \,2\).

- Diện tích hình chữ nhật = chiều dài \( \times \) chiều rộng.

Lời giải chi tiết :

Chu vi hình \(1\) là:                 \((9 + 4) \times 2 = 26\,\,(cm)\)

Diện tích hình \(1\) là:             \(9 \times 4 = 36\,\,(c{m^2})\)

Chu vi hình \(2\) là:                 \(6 \times 4 = 24\,\,(cm)\)

Diện tích hình \(2\) là:             \(6 \times 6 = 36\,\,(c{m^2})\)

Ta có \(26cm > 24cm\) nên  chu vi hình \(1\) lớn hơn chu vi hình \(2\).

          \(36c{m^2} = 36c{m^2}\) nên diện tích hình \(1\) bằng diện tích hình \(2\).

Vậy các kết luận đúng là b và d; kết luận sai là a và c.

Câu 16 :

Tính diện tích mảnh đất có kích thước như hình vẽ như bên dưới:

A. \(280{m^2}\)

B. \(336{m^2}\)

C. \(448{m^2}\)

D. \(560{m^2}\)

Đáp án

D. \(560{m^2}\)

Phương pháp giải :

Chia mảnh đất đã cho thành các mảnh đất nhỏ mà có thể dễ dàng tính được diện tích các mảnh đó. Diện tích mảnh đất ban đầu bằng tổng diện tích các mảnh đất nhỏ.

Lời giải chi tiết :

Chia mảnh đất đã cho thành \(3\) mảnh đất hình chữ nhật như sau:

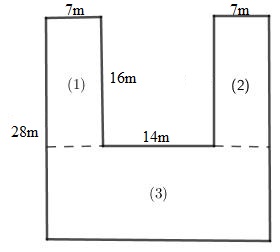
Gọi \(S\) là diện tích mảnh đất ban đầu, \({S_1},\,\,{S_2},\,\,{S_3}\) lần lượt là diện tích các mảnh đất \((1),\,(2),\,(3)\) . Khi đó \(S = {S_1} + {S_2} + {S_3}\).

Diện tích mảnh đất thứ nhất là:

            \(16 \times 7 = 112\,\,({m^2})\)

Diện tích mảnh đất thứ hai là:

            \(16 \times 7 = 112\,\,({m^2})\)

Chiều rộng của mảnh đất thứ ba là:

            \(28 - 16 = 12\,\,(m)\)

Chiều dài của mảnh đất thứ ba là:

            \(7 + 14 + 7 = 28\,\,(m)\)

Diện tích mảnh đất thứ ba là:

            $28 \times 12 = 336\,\,({m^2})$

Diện tích mảnh đất ban đầu là:

             $112 + 112 + 336 = 560\,\,({m^2})$

                                    Đáp số: \(560{m^2}\)

Trắc nghiệm Bài 78: Ôn tập phân số và các phép tính Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 78: Ôn tập phân số và các phép tính Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 78: Ôn tập số tự nhiên và các phép tính Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 78: Ôn tập số tự nhiên và các phép tính Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 77: Em làm được những gì Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 77: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 76: Tìm phân số của một số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 76: Tìm phân số của một số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 75: Phép chia phân số mẫu số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 75: Phép chia phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 74: Phép nhân phân số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 74: Phép nhân phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 73: Em làm được những gì Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 73: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 72: Trừ hai phân số khác mẫu số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 72: Trừ hai phân số khác mẫu số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 71: Trừ hai phân số cùng mẫu số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 71: Trừ hai phân số cùng mẫu số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 70: Em làm được những gì Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 70: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 69: Cộng hai phân số khác mẫu số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 69: Cộng hai phân số khác mẫu số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 68: Cộng hai phân số cùng mẫu số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 68: Cộng hai phân số cùng mẫu số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 67: Em làm được những gì Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 67: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 66: So sánh hai phân số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 66: So sánh hai phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 65: Quy đồng mẫu số các phân số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 65: Quy đồng mẫu số các phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 64: Em làm được những gì Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 64: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 63: Rút gọn phân số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 63: Rút gọn phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 62: Phân số bằng nhau Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 62: Phân số bằng nhau Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 61: Phân số và phép chia số tự nhiên Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 61: Phân số và phép chia số tự nhiên Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết
Trắc nghiệm Bài 60: Phân số Toán 4 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 60: Phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store