Lý thuyết Số vô tỉ. Căn bậc hai số học SGK Toán 7 Chân trời sáng tạo

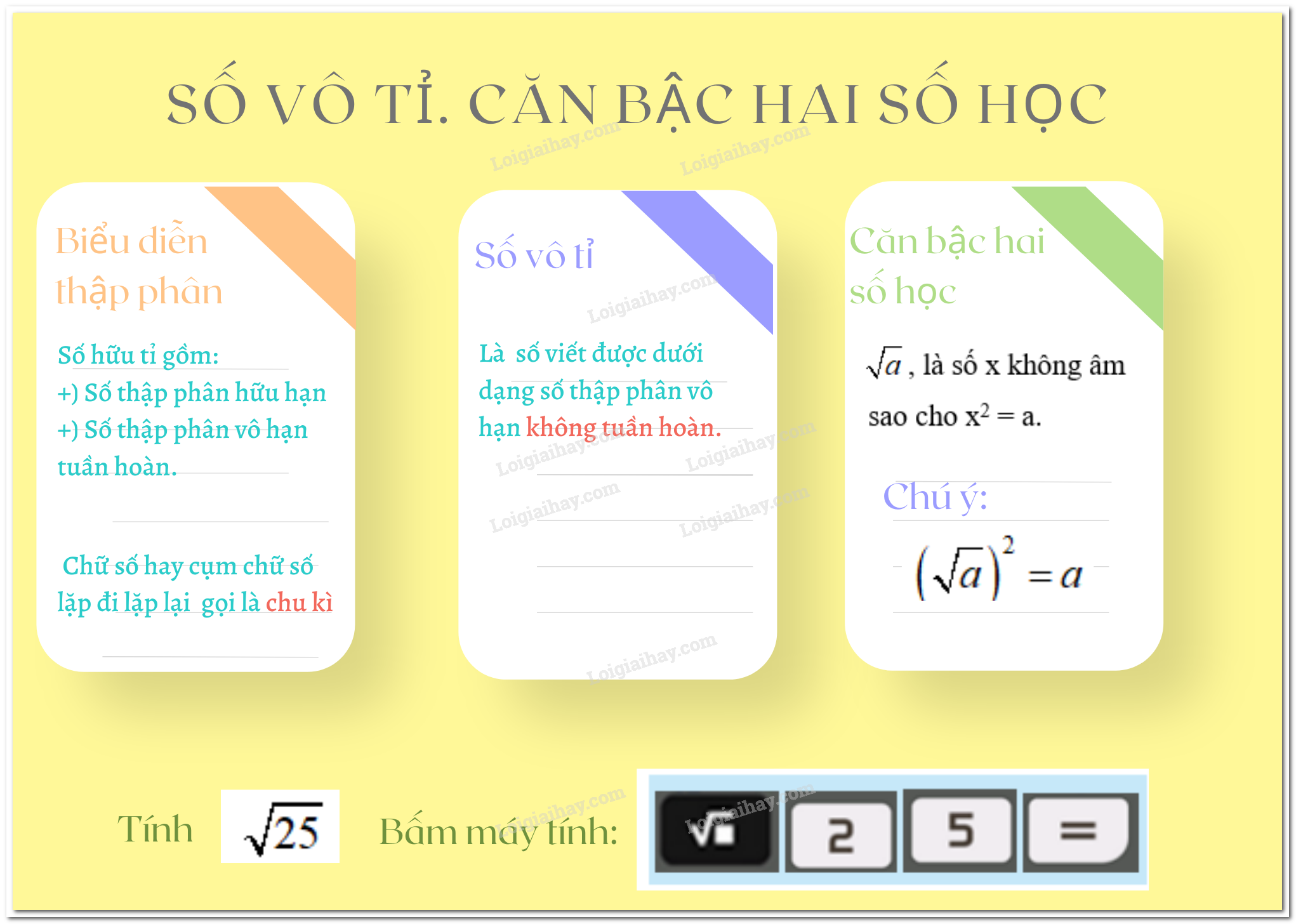
1. Biểu diễn thập phân của một số hữu tỉ

Tổng hợp đề thi giữa kì 1 lớp 7 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên

1. Biểu diễn thập phân của một số hữu tỉ

Ví dụ: Các số thập phân đã học như -4,3 ; 0,35;… còn được gọi là số thập phân hữu hạn.

Các số -0,2(7) ; 1,3(18) ; 5,(1) ;…. là những số thập phân vô hạn tuần hoàn với chu kì lần lượt là 7 ; 18 ; 1.

+ Mỗi số thập phân vô hạn tuần hoàn biểu diễn 1 số hữu tỉ. Chữ số hay cụm chữ số lặp đi lặp lại được gọi là chu kì.

Chú ý:

+ Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

+ Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

Ví dụ: \(\frac{3}{{80}} = \frac{3}{{{2^4}.5}} = \frac{{{{3.5}^3}}}{{{2^4}{{.5.5}^3}}} = \frac{{375}}{{10000}} = 0,0375\)

+ Nếu phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

Ví dụ: \(\frac{7}{{30}} = 0,2333.... = 0,2(3)\)

2. Số vô tỉ

Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

Ví dụ: \(\pi = 3,1415926.....;e = 2,71828.....;....\)là những sô vô tỉ

Tập hợp các số vô tỉ được kí hiệu là I

3. Căn bậc hai số học

Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \), là số x không âm sao cho x² = a.

Ví dụ: \(\sqrt {121} = 11\) vì 11 > 0 và 11² = 121

Chú ý: Cho \(a \ge 0\). Khi đó:

+ Đẳng thức \(\sqrt a = b\) đúng nếu \(b \ge 0;{b^2} = a\)

+ \({\left( {\sqrt a } \right)^2} = a\)

4. Tính căn bậc hai số học bằng máy tính cầm tay

Ví dụ: Tính \(\sqrt {25} \)

Ta bấm liên tiếp các nút:

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 13 phiếu

Bài tiếp theo

Giải mục 1 trang 30, 31 SGK Toán 7 tập 1 - Chân trời sáng tạo
Hãy thực hiện các phép chia sau đây:...Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân:...Hãy so sánh hai số hữu tỉ:
Giải mục 2 trang 31, 32 SGK Toán 7 tập 1 - Chân trời sáng tạo
Cho hai hình vuông ABCD và AMBN như hình bên. Cho biết cạnh AM=1 dm. - Em hãy cho biết diện tích hình vuông ABCD gấp mấy lần diện tích hình vuông AMBN. - Tính diện tích hình vuông ABCD. - Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
Giải mục 3 trang 32 SGK Toán 7 tập 1 - Chân trời sáng tạo
a) Tìm giá trị của x2 với x lần lượt bằng 2; 3; 4; 5; 10. b) Tìm số thực không âm x với x2 lần lượt bằng 4; 9; 16; 25; 100..Viết các căn bậc hai số học của: 16; 7; 10; 36..
Giải mục 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút...Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
Giải bài 1 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo
a) Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân: b) Trong các số thập phân vừa tính được, hãy chỉ ra các số thập phân vô hạn tuần hoàn.
Giải bài 2 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo
Chọn phát biểu đúng trong các phát biểu sau:
Giải bài 3 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo
Tính:
Giải bài 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo
Hãy thay dấu ? bằng các số thích hợp.
Giải bài 5 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo
Dùng máy tính cầm tay để tính các căn bậc hai số học sau (làm tròn đến 3 chữ số thập phân).
Giải bài 6 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo
Bác Thu thuê thợ lát gạch một cái sân hình vuông hết tất cả là 10 125 000 đồng. Cho biết chi phí cho 1 m2 (kể cả công thợ và vật liệu) là 125 000 đồng. Hãy tính chiều dài cạnh của cái sân.
Giải bài 7 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo
Tính bán kính của một hình tròn có diện tích là 9869 m2 (dùng máy tính cầm tay).
Giải bài 8 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo
Tìm số hữu tỉ trong các số sau: