 Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
 Bài 17. Dấu của tam thức bậc hai Toán 10 Kết nối tri thức
Bài 17. Dấu của tam thức bậc hai Toán 10 Kết nối tri thức
Lý thuyết Dấu của tam thức bậc hai - SGK Toán 10 Kết nối tri thức
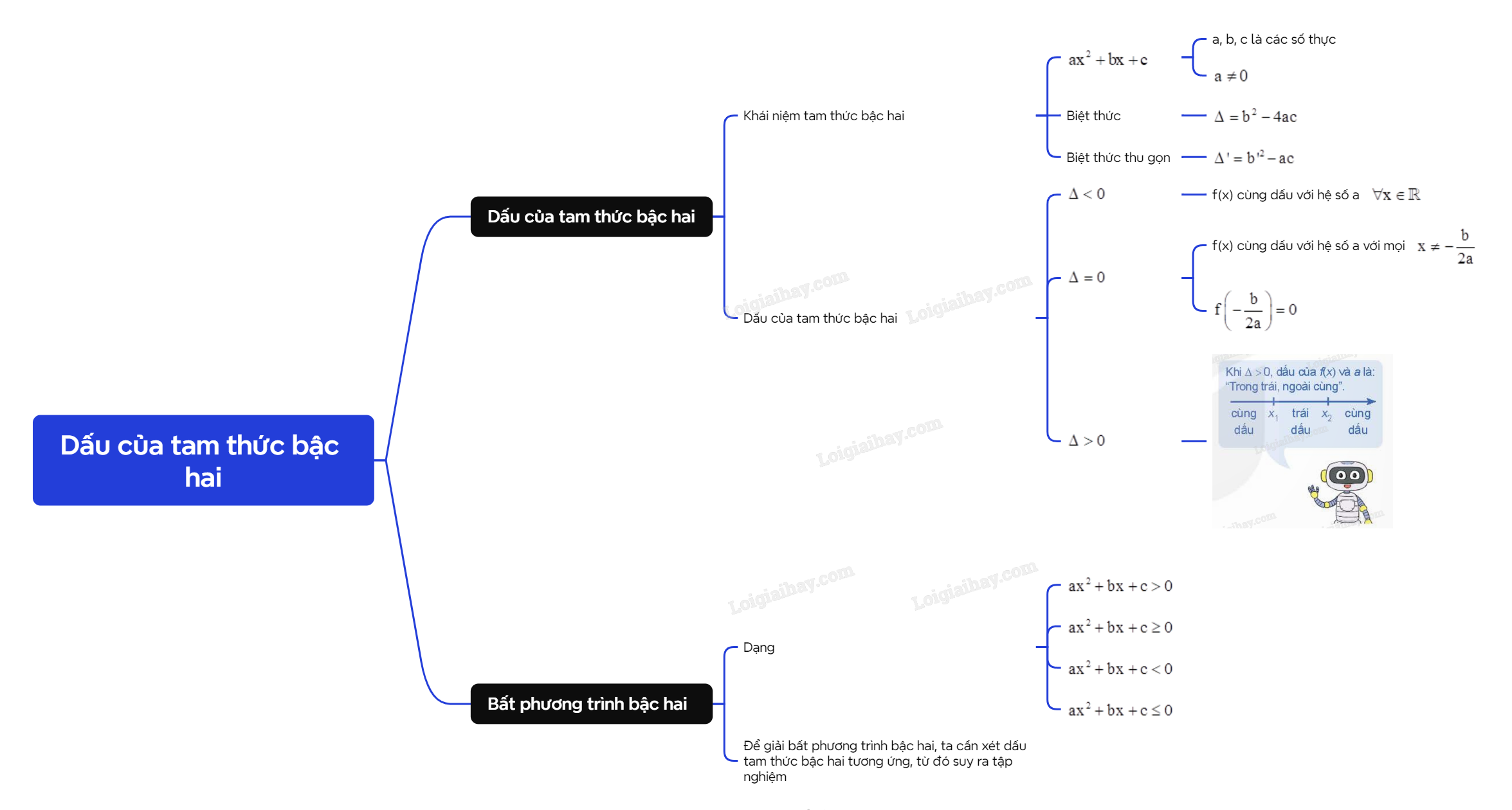
A. Lý thuyết 1. Dấu của tam thức bậc hai a) Khái niệm tam thức bậc hai
A. Lý thuyết
1. Dấu của tam thức bậc hai
a) Khái niệm tam thức bậc hai
| Tam thức bậc hai (đối với x) là biểu thức có dạng \(a{x^2} + bx + c\), trong đó a, b, c là các số thực cho trước và \(a \ne 0\), được gọi là các hệ số của tam thức bậc hai. |
Chú ý: Nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) cũng được gọi là nghiệm của tam thức bậc hai \(a{x^2} + bx + c\).
| \(\Delta = {b^2} - 4ac\) và \(\Delta ' = b{'^2} - ac\) với b = 2b’ tương ứng được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai \(a{x^2} + bx + c\). |
b) Dấu của tam thức bậc hai
Mối quan hệ giữa dấu của tam thức bậc hai \(a{x^2} + bx + c\) với dấu của hệ số a trong từng trường hợp của \(\Delta \) được phát biểu trong định lí về dấu của tam thức bậc hai sau đây:
|
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\) \((a \ne 0)\). - Nếu \(\Delta < 0\) thì f(x) cùng dấu với hệ số a \(\forall x \in \mathbb{R}\). - Nếu \(\Delta = 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \ne - \frac{b}{{2a}}\) và \(f\left( { - \frac{b}{{2a}}} \right) = 0\). - Nếu \(\Delta > 0\) thì tam thức f(x) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) \(({x_1} < {x_2})\). Khi đó: + f(x) cùng dấu với hệ số a \(\forall x \in ( - \infty ;{x_1}) \cup ({x_2}; + \infty )\). + f(x) trái dấu với hệ số a \(\forall x \in ({x_1};{x_2})\). |

Chú ý: Trong định lí về dấu của tam thức bậc hai, có thể thay \(\Delta \) bởi \(\Delta '\).
2. Bất phương trình bậc hai
|
Bất phương trình bậc hai ẩn x là bất phương trình có dạng \(a{x^2} + bx + c > 0\) (hoặc \(a{x^2} + bx + c \ge 0\), \(a{x^2} + bx + c < 0\), \(a{x^2} + bx + c \le 0\)), trong đó a, b, c là những số thực đã cho và \(a \ne 0\). Số thực \({x_0}\) gọi là nghiệm của bất phương trình bậc hai \(a{x^2} + bx + c > 0\), nếu \(a{x_0}^2 + b{x_0} + c > 0\). Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai \(a{x^2} + bx + c > 0\) gọi là tập nghiệm của bất phương trình này. Giải một bất phương trình bậc hai là tìm tập nghiệm của nó. |
Nhận xét: Để giải bất phương trình bậc hai \(a{x^2} + bx + c > 0\) (hoặc \(a{x^2} + bx + c \ge 0\), \(a{x^2} + bx + c < 0\), \(a{x^2} + bx + c \le 0\)) ta cần xét dấu tam thức \(a{x^2} + bx + c\), từ đó suy ra tập nghiệm.
B. Bài tập
Bài 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai?
A. \(3x + 2\sqrt x + 1\)
B. \( - 5{x^4} + 3{x^2} + 4\)
C. \( - \frac{2}{3}{x^2} + 7x - 4\)
D. \({\left( {\frac{1}{x}} \right)^2} + 2\frac{1}{x} + 3\)
Giải:
\( - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai với \(a = - \frac{2}{3},b = 7,c = - 4\).
Bài 2: Xét dấu các tam thức bậc hai sau đây:
a) \({x^2} + x + 1\).
b) \( - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\).
c) \(2{x^2} + 6x - 8\).
Giải:
a) \(f(x) = {x^2} + x + 1\) có \(\Delta = - 3 < 0\) và \(a = 1 > 0\) nên f(x) > 0 với mọi \(x \in \mathbb{R}\).
b)
\(f(x) = - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\) có \(\Delta = 0\) và \(a = - \frac{3}{2} < 0\) nên f(x) có nghiệm kép x = 3 và f(x) < 0 với mọi \(x \ne 3\).
c) Dễ thấy \(f(x) = 2{x^2} + 6x - 8\) có \(\Delta ' = 25 > 0\), a = 2 > 0 và có hai nghiệm phân biệt \({x_1} = - 4\), \({x_2} = 1\). Do đó ta có bảng xét dấu:
Suy ra f(x) > 0 với mọi \(x \in ( - \infty ; - 4) \cup (1; + \infty )\) và f(x) < 0 với mọi \(x \in ( - 4;1)\).
Bài 3: Giải các bất phương trình sau:
a) \(3{x^2} + x + 5 \le 0\).
b) \( - 3{x^2} + 2\sqrt 3 x - 1 \ge 0\).
c) \( - {x^2} + 2x + 1 > 0\).
Giải:
a) Tam thức \(f(x) = 3{x^2} + x + 5\) có \(\Delta = - 59 < 0\), hệ số a = 3 > 0 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là \(3{x^2} + x + 5 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình vô nghiệm.
b) Tam thức \(f(x) = - 3{x^2} + 2\sqrt 3 x - 1\) có \(\Delta ' = 0\), hệ số a = -3 < 0 nên f(x) có nghiệm kép \(x = \frac{{\sqrt 3 }}{3}\) và f(x) luôn âm (cùng dấu với a) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\), tức là \( - 3{x^2} + 2\sqrt 3 x - 1 < 0\) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\).
Suy ra bất phương trình có nghiệm duy nhất \(x = \frac{{\sqrt 3 }}{3}\).
c) Tam thức \(f(x) = - {x^2} + 2x + 1\) có \(\Delta ' = 2 > 0\) nên f(x) có hai nghiệm \({x_1} = 1 - \sqrt 2 \) và \({x_2} = 1 + \sqrt 2 \).
Mặt khác, a = -1 < 0, do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là \(S = \left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\).
- Giải mục 1 trang 19, 20, 21, 22 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải mục 2 trang 22, 23 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải bài 6.15 trang 24 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.16 trang 24 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.17 trang 24 SGK Toán 10 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức












Danh sách bình luận