Giải mục 1 trang 19, 20, 21, 22 SGK Toán 10 tập 2 - Kết nối tri thức

HĐ1

Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:

\(A = 0,5{x^2}\);

\(B = 1 - {x^2}\);  

\(C = {x^2} + x + 1\);     

\(D = (1 - x)(2x + 1)\).

Lời giải chi tiết:

Ta có:

\(A = 0,5{x^2}\);

\(B = 1 - {x^2}\);

\(C = {x^2} + x + 1\);

\(D = (1 - x)(2x + 1) = 2x + 1 - 2{x^2} - x =  - 2{x^2} + x + 1\).

Các biểu thức đều có dạng \(a{x^2} + bx + c\) \((a \ne 0)\) với a, b, c là các số thực.

LT1

Hãy cho biết biểu thức nào sau đây là tam thức bậc hai.

\(A = 3x + 2\sqrt x  + 1\);

\(B =  - 5{x^4} - 3{x^2} + 4\);

\(C =  - \frac{2}{3}{x^2} + 7x - 4\);

\(D = {\left( {\frac{1}{x}} \right)^2} + 2.\frac{1}{x} + 3\).

Phương pháp giải:

Tam thức bậc hai là biểu thức có dạng \(a{x^2} + bx + c\), trong đó a, b, c là những số cho trước \(\left( {a \ne 0} \right)\).

Lời giải chi tiết:

Biểu thức \(C =  - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai.

Biểu thức A không là tam thức bậc hai vì chứa \(\sqrt x \).

Biểu thức B không là tam thức bậc hai vì chứa \({x^4}\).

Biểu thức D không là tam thức bậc hai vì chứa \({\left( {\frac{1}{x}} \right)^2}\).

HĐ2

Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\).

a) Xác định hệ số a. Tính \(f(0)\); \(f(1)\); \(f(2)\); \(f(3)\); \(f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số \(a\).

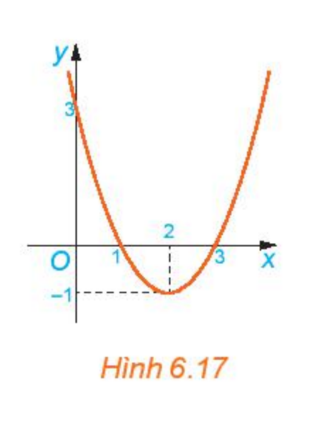
b) Cho đồ thị hàm số \(y = f(x)\) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?

c) Nhận xét về dấu của \(f(x)\) và dấu của hệ số \(a\) trên từng khoảng đó.

Lời giải chi tiết:

a) Hệ số a là: a = 1.

\(f(0) = {0^2} - 4.0 + 3 = 3\);

\(f(1) = {1^2} - 4.1 + 3 = 0\);

\(f(2) = {2^2} - 4.2 + 3 =  - 1\);

\(f(3) = {3^2} - 4.3 + 3 = 0\);

\(f(4) = {4^2} - 4.4 + 3 = 3\).

Ta thấy f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a.

b) Nhìn vào đồ thị ta thấy:

- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành.

- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành.

- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành.

c)

- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành \(\Rightarrow f(x) > 0\), cùng dầu với hệ số a.

- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành \(\Rightarrow f(x) < 0\), khác dấu với hệ số a.

- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành \(\Rightarrow f(x) > 0\), cùng dấu với hệ số a.

HĐ3

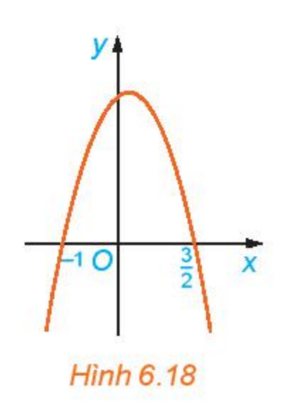
Cho đồ thị hàm số \(y = g(x) =  - 2{x^3} + x + 3\) như Hình 6.18.

a) Xét trên từng khoảng \(\left( { - \infty ; - 1} \right),\left( { - 1;\frac{3}{2}} \right),\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía trên trục Ox hay nằm phía dưới trục Ox.

b) Nhận xét về dấu của g(x) và dấu của hệ số a trên từng khoảng đó.

Lời giải chi tiết:

Ta có: hệ số a = -2 < 0.

a) Nhìn vào đồ thị ta thấy:

- Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành.

- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành.

- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành.

c) - Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành \(\Rightarrow f(x) < 0\), cùng dầu với hệ số a.

- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành \(\Rightarrow f(x) > 0\), khác dấu với hệ số a.

- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành \(\Rightarrow f(x) < 0\), cùng dấu với hệ số a.

HĐ4

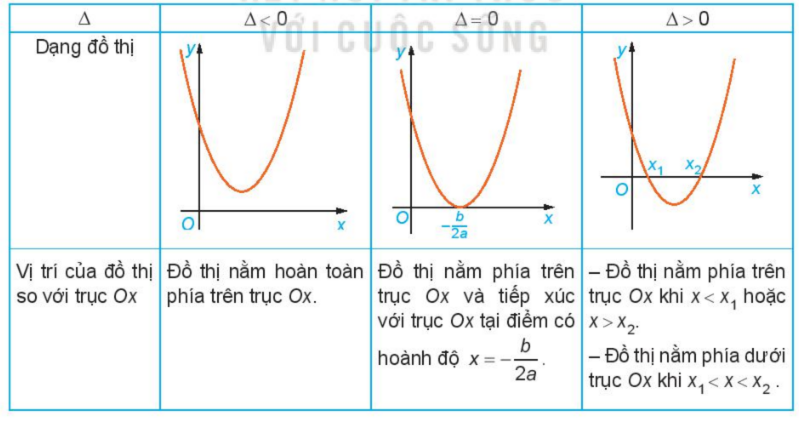
Nêu nội dung thay vào các ô có dấu “?” trong bảng sau cho thích hợp

Trường hợp a > 0:

Trường hợp a < 0:

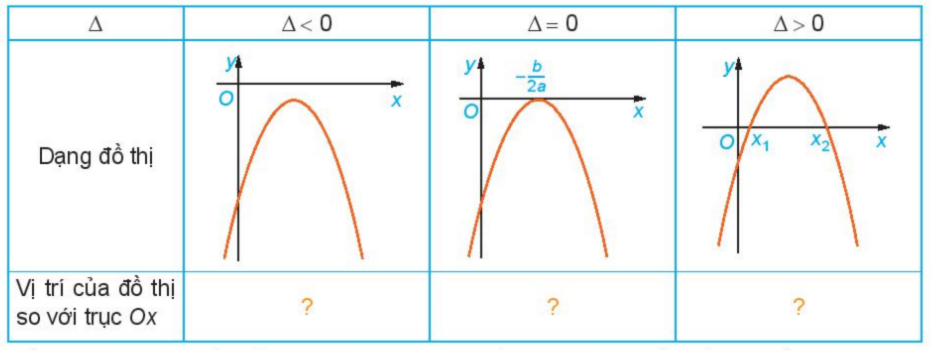
Lời giải chi tiết:

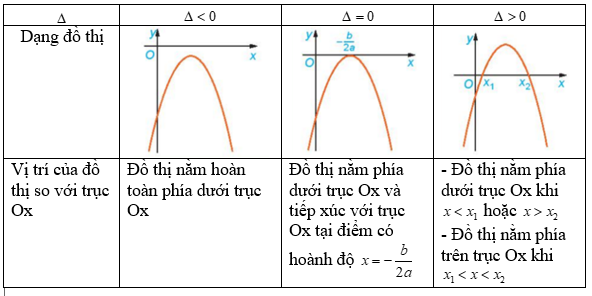
LT2

Xét dấu các tam thức bậc hai sau:

a) \( - 3{x^2} + x - \sqrt 2 \);

b) \({x^2} + 8x + 16\);

c) \( - 2{x^2} + 7x - 3\).

Phương pháp giải:

Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\):

Bước 1: Tính \(\Delta  = {b^2} - 4ac\).

Bước 2:

- Nếu \(\Delta  < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\).

- Nếu \(\Delta  = 0\) thì \(f(x)\) có nghiệm kép là \({x_0}\) . Vậy \(f(x)\) cùng dấu với a với \(x \ne {x_0}\).

- Nếu \(\Delta  > 0\) thì \(f(x)\) có 2 nghiệm là \({x_1};{x_2}\) \(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết:

a) \(f(x) =  - 3{x^2} + x - \sqrt 2 \)có \(\Delta  = 1 - 12\sqrt 2  < 0\) và \(a = -3\).

b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta  = 0\) và \(a = 1 > 0\) nên \(g(x)\) có nghiệm kép \(x =  - 4\) và \(g(x) > 0\) với mọi \(x \ne  - 4\).

c) \(h(x) =  - 2{x^2} + 7x - 3\) có \(\Delta  = 25 > 0\) và \(a = -2\).

Do đó ta có bảng xét dấu \(h(x)\):

Suy ra \(h(x) > 0\) với mọi \(x \in \left( {\frac{1}{2};3} \right)\).