 Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
 Bài 17. Dấu của tam thức bậc hai Toán 10 Kết nối tri thức
Bài 17. Dấu của tam thức bậc hai Toán 10 Kết nối tri thức
Giải mục 2 trang 22, 23 SGK Toán 10 tập 2 - Kết nối tri thức
Trở lại tình huống mở đầu. Với yêu cầu mảnh đất được rào chắn có diện tích không nhỏ hơn 48 ({m^2}), hãy viết bất đẳng thức thể hiện sự so sánh biểu thức tính diện tích Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai
HĐ5
Trở lại tình huống mở đầu. Với yêu cầu mảnh đất được rào chắn có diện tích không nhỏ hơn 48 \({m^2}\), hãy viết bất đẳng thức thể hiện sự so sánh biểu thức tính diện tích \(S(x) = - 2{x^2} + 20x\) với 48.
Lời giải chi tiết:
Để diện tích của mảnh vườn không nhỏ hơn 48 \({m^2}\) thì:
\(S(x) \ge 48 \Rightarrow - 2{x^2} + 20x \ge 48\)
\(\Leftrightarrow - 2{x^2} + 20x - 48 \ge 0\).
LT3
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\);
b) \({x^2} - 8x + 16 \le 0\);
c) \({x^2} - x - 6 > 0\).
Phương pháp giải:
Để giải bất phương trình bậc hai, ta cần xét dấu tam thức \(f(x) = a{x^2} + bx + c\) \((a \ne 0)\) từ đó suy ra tập nghiệm.
Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\).
Bước 1: Tính \(\Delta = {b^2} - 4ac\).
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\).
- Nếu \(\Delta = 0\) thì \(f(x)\) có nghiệm kép là \({x_0}\). Vậy \(f(x)\) cùng dấu với a với \(x \ne {x_0}\).
- Nếu \(\Delta > 0\) thì \(f(x)\) có 2 nghiệm là \({x_1};{x_2}\)\(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết:
a) Tam thức \(f(x) = - 5{x^2} + x - 1\) có \(\Delta = - 19 < 0\), hệ số \(a = - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta = 0\), hệ số a = 1 > 0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\).
Suy ra bất phương trình có nghiệm duy nhất là x = 4.
c) Tam thức $f(x) = x^2 - x - 6$ có $\Delta = (-1)^2 - 4 \cdot 1 \cdot (-6) = 25 > 0$ nên $f(x)$ có hai nghiệm $x_1 = -2$ và $x_2 = 3$.
Mặt khác hệ số $a = 1 > 0$, do đó ta có bằng xét dấu sau:

Tập nghiệm của bất phương trình là $S = (-\infty; -2) \cup (3; +\infty)$.
VD
Độ cao so với mặt đất của một quả bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai \(h(t) = - 4,9{t^2} + 20t + 1\), ở độ cao \(h(t)\) tính bằng mét và thời gian t tình bằng giây. Trong khoảng thời điểm nào trong quá trình bay của nó, quả bóng sẽ ở độ cao trên 5 m so với mặt đất.
Phương pháp giải:
Tìm khoảng thời gian t để \(h(t) > 5\), bài toán đưa về xét dấu tam thức \(f(t) = h(t) - 5\).
Các bước xét dấu tam thức bậc hai \(f(t) = a{t^2} + bt + c\).
Bước 1: Tính \(\Delta = {b^2} - 4ac\).
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(t)\) luôn cùng dấu với a với mọi \(t \in \mathbb{R}\).
- Nếu \(\Delta = 0\) thì \(f(t)\) có nghiệm kép là \({t_0}\). Vậy \(f(t)\) cùng dấu với a với \(t \ne {t_0}\).
- Nếu \(\Delta > 0\) thì \(f(t)\) có 2 nghiệm là \({t_1};{t_2}\)\(({t_1} < {t_2})\). Ta lập bảng xét dấu.

Kết luận khoảng chứa t thỏa mãn \(f(t) > 0\).
Lời giải chi tiết:
Để quả bóng ở độ cao trên 5 m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\) có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\) nên \(f(t)\) có 2 nghiệm:
\(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau:
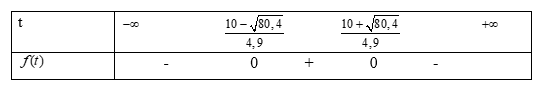
Do đó để \(h(t) > 5\) thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\).
Vậy để quả bóng sẽ ở độ cao trên 5 m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\).
- Giải bài 6.15 trang 24 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.16 trang 24 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.17 trang 24 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.18 trang 24 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.19 trang 24 SGK Toán 10 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức












Danh sách bình luận