Toán 10, giải toán lớp 10 chân trời sáng tạo Bài 3. Các phép toán trên tập hợp Toán 10 Chân trời sán..

Lý thuyết Các phép toán trên tập hợp - SGK Toán 10 Chân trời sáng tạo


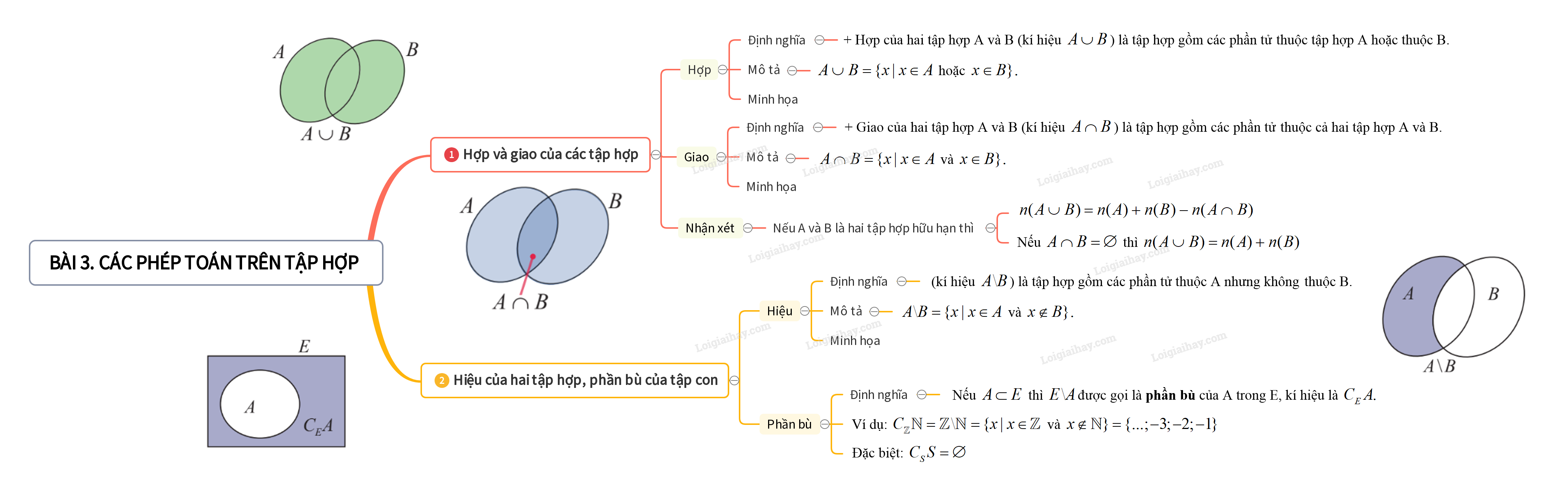
1. Hợp và giao của các tập hợp 2. Hiệu của hai tập hợp, phần bù của tập con

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

1. Hợp và giao của các tập hợp

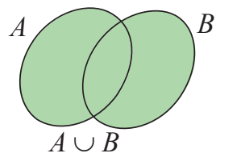
+ Hợp của hai tập hợp A và B (kí hiệu \(A \cup B\)) là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc T.

\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} .\)

 

+ Giao của hai tập hợp A và B (kí hiệu \(A \cap B\)) là tập hợp gồm các phần tử thuộc cả hai tập hợp A và B.

\(A \cap B = \{ x|x \in A\) và \(x \in B\} .\)

 

+ Nhận xét: Nếu A và B là hai tập hợp hữu hạn thì

\(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)

Nếu \(A \cap B = \emptyset \) thì \(n(A \cup B) = n(A) + n(B)\)

 

2.  Hiệu của hai tập hợp, phần bù của tập con

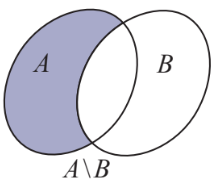
Hiệu của hai tập hợp A và B (kí hiệu \(A{\rm{\backslash }}B\)) là tập hợp gồm các phần tử thuộc A nhưng không thuộc B.

\(A{\rm{\backslash }}B = \{ x|x \in A\) và \(x \notin B\} .\)

 

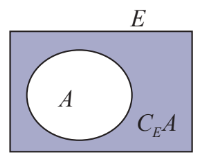
Nếu \(A \subset E\) thì \(E{\rm{\backslash }}A\)được gọi là phần bù của A trong E, kí hiệu là \({C_E}A.\)

 

Ví dụ: \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và \(x \notin \mathbb{N}\}  = \{ ...; - 3; - 2; - 1\} \)

Đặc biệt: \({C_S}S = \emptyset \)


Bình chọn:
4 trên 8 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store