Toán 10, giải toán lớp 10 chân trời sáng tạo Bài 3. Các phép toán trên tập hợp Toán 10 Chân trời sán..

Giải mục 2 trang 23, 24, 25 SGK Toán 10 tập 1 - Chân trời sáng tạo


Cho tập hợp E ={ x thuộc N |x < 8} ,A = { 0;1;2;3;4} ,B = { 3;4;5} Xác định các tập hợp sau đây:

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 2

Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.

a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.

b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.

Phương pháp giải:

Viết tập hợp bằng cách liệt kê các phần tử.

Lời giải chi tiết:

a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: \(E = \{ {a_2};{a_7}\} \)

b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: \(F = \{ {a_3};{a_4};{a_9}\} \)

Thực hành 3

Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)

Xác định các tập hợp sau đây:

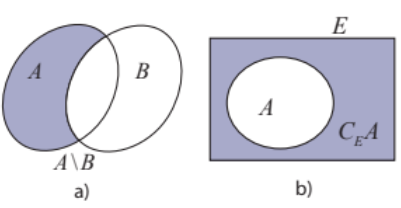
a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\)

b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\)

c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\)

Phương pháp giải:

Lời giải chi tiết:

\(E = \{ x \in \mathbb{N}|x < 8\}  = \{ 0;1;2;3;4;5;6;7\} \)

a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)

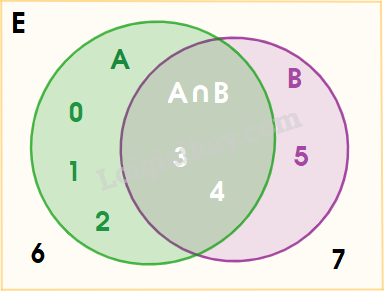
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)

\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\}  \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)

c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)

\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\}  \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)

Thực hành 4

Xác định các tập hợp sau đây:

a) \((1;3) \cup [ - 2;2]\)

b) \(( - \infty ;1) \cap [0;\pi ]\)

c) \([\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\)

d) \({C_\mathbb{R}}[ - 1; + \infty )\)

Phương pháp giải:

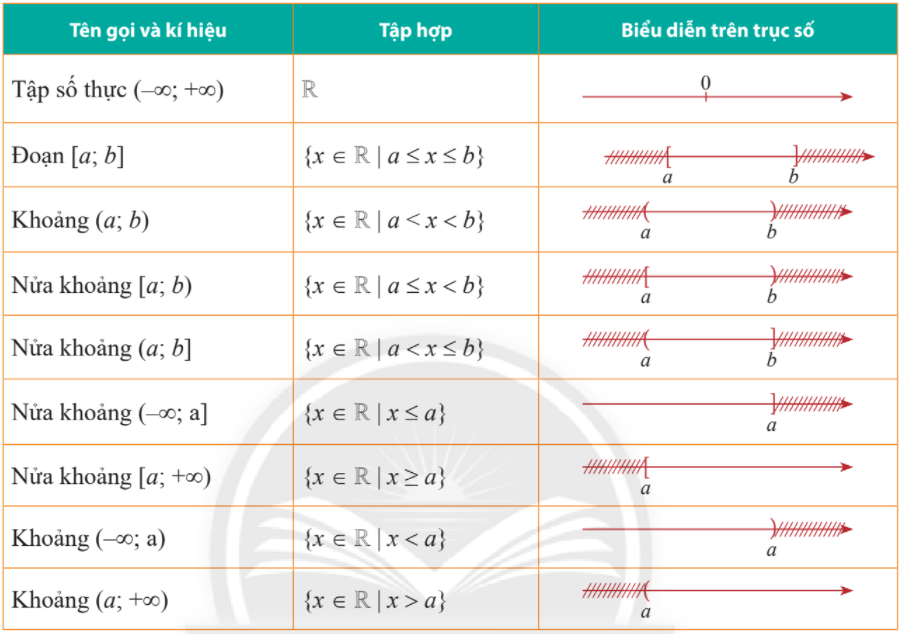
Biểu diễn các tập hợp trên trục số

Lời giải chi tiết:

a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:

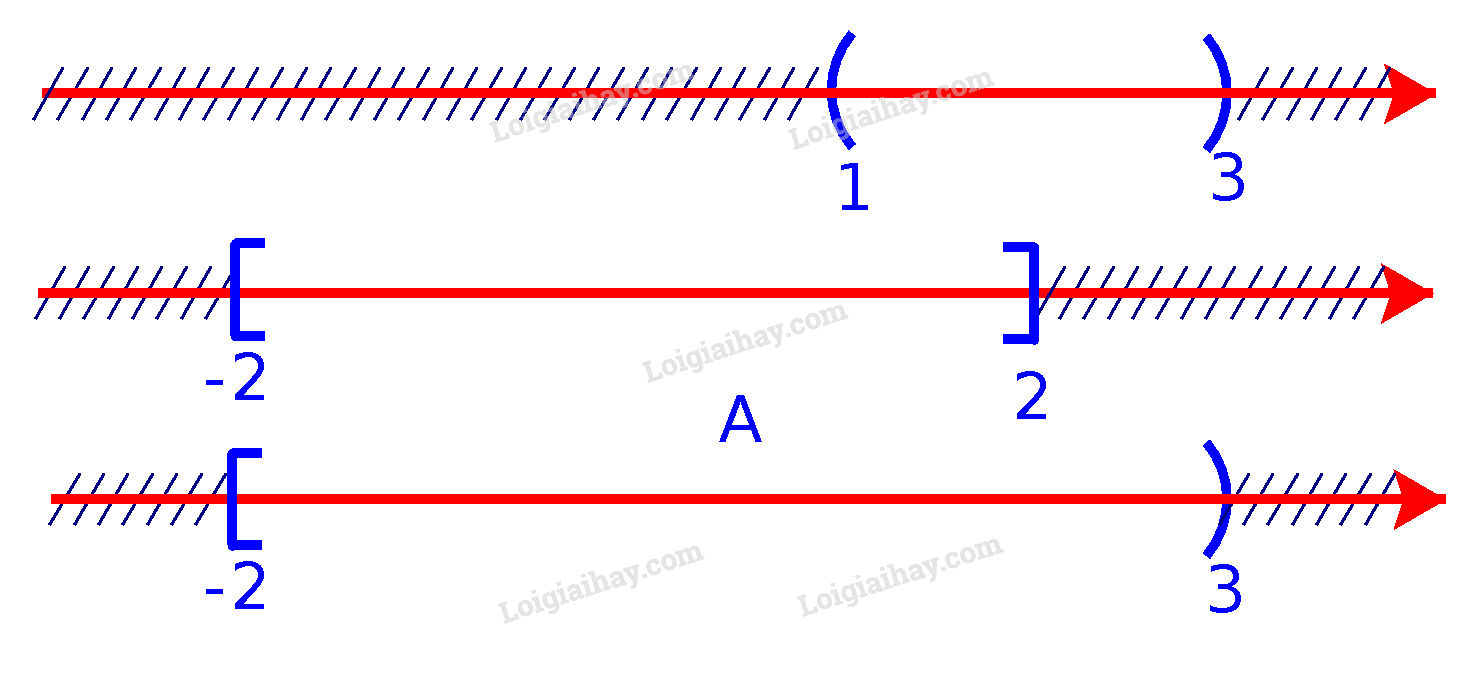
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)

b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:

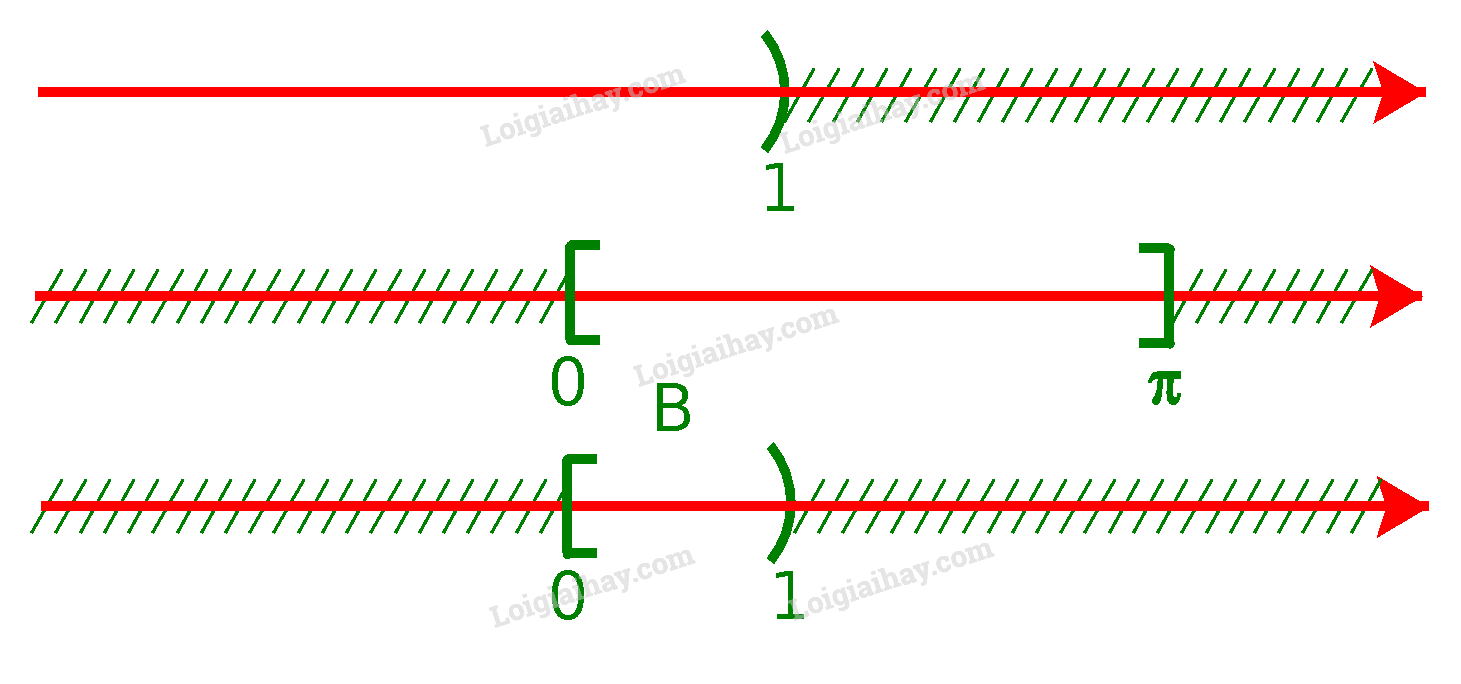
Từ sơ đồ, ta thấy \(B = [0;1)\)

 c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:

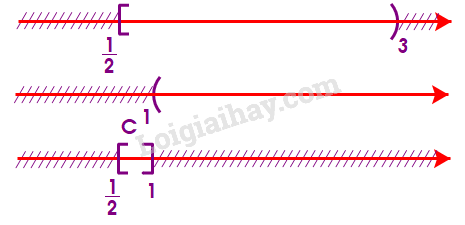
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)

d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:

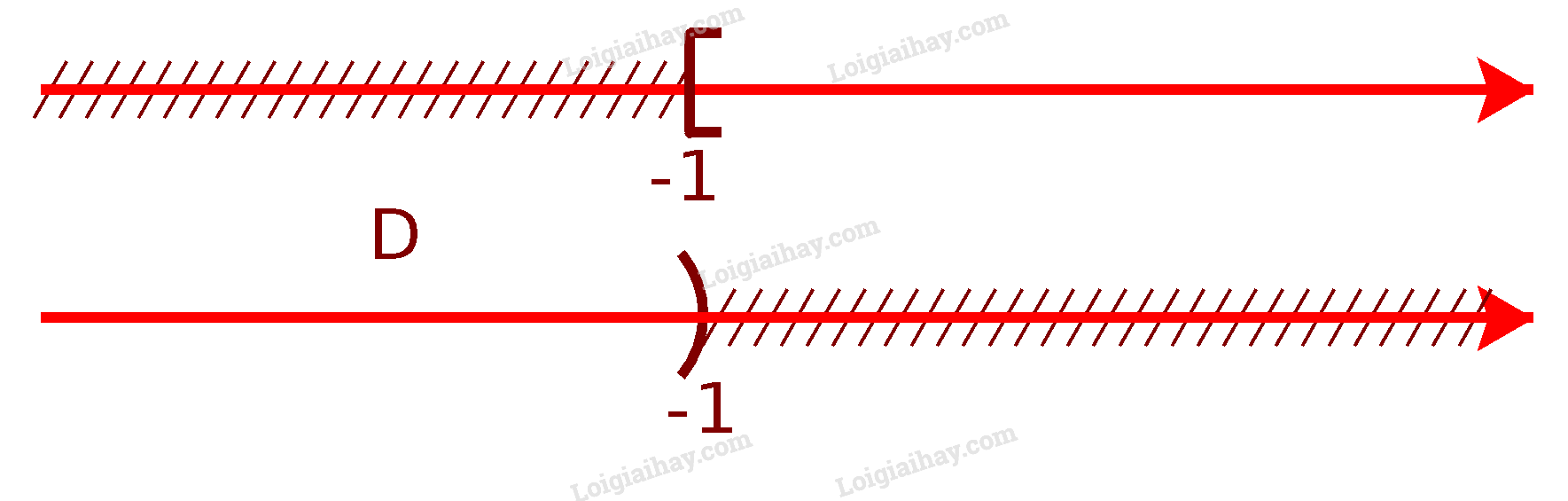
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)


Bình chọn:
4.5 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store