-
GIẢI SGK TOÁN 11 CÁNH DIỀU - MỚI NHẤT
-
Toán 10 tập 1 - Cánh diều
-
Toán 10 tập 2 - Cánh diều
Giải bài 6 trang 61 SGK Toán 10 tập 1 – Cánh diều
Lập bảng xét dấu của mỗi tam thức bậc hai sau
Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
b) \(f\left( x \right) = {x^2} - x - 12\)
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
Phương pháp giải - Xem chi tiết
Bước 1: Tìm nghiệm của \(f\left( x \right) = 0\) và hệ số a.
Bước 2: Lập bảng xét dấu.
Lời giải chi tiết
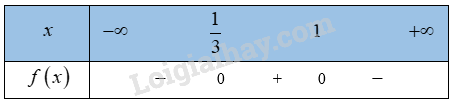
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:
b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:
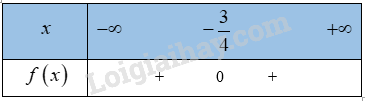
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
Bình luận
Chia sẻ
- Giải bài 7 trang 61 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 8 trang 61 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 5 trang 61 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí
>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
