Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụn..

Giải bài 6 trang 43 SGK Toán 10 tập 1 – Cánh diều

Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch.

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

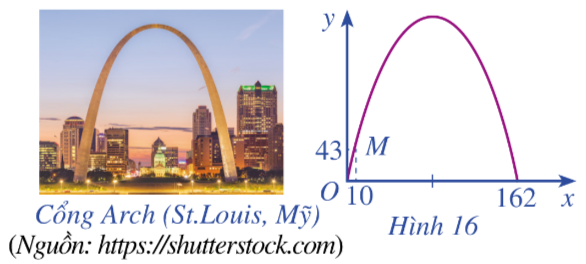
Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có toạ độ (162;0). Biết một điểm M trên cổng có toạ độ là (10;43). Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.

Phương pháp giải - Xem chi tiết

- Xác định các điểm thuộc đồ thị.

- Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)

- Thay tọa độ các điểm vào và tìm a, b, c.

- Tìm đỉnh của parabol, từ đó suy ra chiều cao của cổng.

Lời giải chi tiết

Từ đồ thị ta thấy các điểm thuộc đồ thị là: \(A\left( {0;0} \right),B\left( {10;43} \right),C\left( {162;0} \right)\).

Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\).

Thay tọa độ các điểm A, B, C vào ta được hệ:

\(\left\{ \begin{array}{l}a{.0^2} + b.0 + c = 0\\a{.10^2} + b.10 + c = 43\\a{.162^2} + b.162 + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\100a + 10b = 43\\{162^2}a + 162b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = - \frac{{43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)

Từ đố ta có \(y = - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\).

Hoành độ đỉnh của đồ thị là: \(x = - \frac{b}{{2a}} = 81\).

Khi đó: \(y = - \frac{{43}}{{1520}}{.81^2} + \frac{{3483}}{{760}}.81 \approx 186\) (m).

Vậy chiều cao của cổng là 186m.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 10 phiếu

Bài tiếp theo

Giải bài 5 trang 43 SGK Toán 10 tập 1 – Cánh diều
Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau
Giải bài 4 trang 43 SGK Toán 10 tập 1 – Cánh diều
Cho đồ thị hàm số bậc hai ở Hình 15.
Giải bài 3 trang 43 SGK Toán 10 tập 1 – Cánh diều
Vẽ đồ thị của mỗi hàm số sau:
Giải bài 2 trang 43 SGK Toán 10 tập 1 – Cánh diều
Xác định parabol y = ax^2 + bx + 4 trong mỗi trường hợp sau:
Giải bài 1 trang 43 SGK Toán 10 tập 1 – Cánh diều
Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định a,b,c lần lượt là hệ số của x^2, hệ số của x và hệ số tự do.
Giải mục III trang 43, 44 SGK Toán 10 tập 1 - Cánh diều
Trong bài toán ở phần mở đầu, độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Giải mục II trang 39, 40, 41, 42 SGK Toán 10 tập 1 - Cánh diều
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
Giải mục I trang 39 SGK Toán 10 tập 1 - Cánh diều
a) Viết công thức xác định hàm số trên về dạng đa thức theo lũy thừa với số mũ giảm dần của x. b) Bậc của đa thức trên bằng bao nhiêu? Cho hai ví dụ về hàm số bậc hai.
Giải câu hỏi khởi động trang 39 SGK Toán 10 tập 1 - Cánh diều
Cầu cảng Sydney là một trong những hình ảnh biểu tượng của thành phố Sydney và nước Australia. Độ cao y(m) của một điểm thuộc vòng cung thành cầu cảng Sydney có thể biểu thị theo độ dài x(m) tính từ chân cầu bên trái dọc theo đường nối với chân cầu bên phải như sau (Hình 10):
Lý thuyết Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - SGK Toán 10 Cánh diều
I. Hàm số bậc hai II. Đồ thị hàm số bậc hai