Giải bài 2.9 trang 23 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Trong một cuộc thi pha chế, mỗi đợi chơi được sử dụng tối đa 12g hương liệu, 9 lít nước và 315g đường để pha chế hai loại nước A và B. Để pha chết 1 lít nước A cần 45g đường, 1 lít nước và 0,5g hương liệu; để pha chế 1 lít nước B cần 15g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất?

Lời giải chi tiết

• Gọi \(x\) và \(y\) lần lượt là số lít nước loại A và B cần pha chế.

Điều kiện: \(x \ge 0,\,\,y \ge 0.\)

Số hương liệu cần dùng để pha chế hai loại lít nước A và B là: \(0,5x + 2y \le 12.\)

Số lít nước cần dùng để pha chế hai loại nước A và B là: \(x + y \le 9.\)

Số g đường cần dùng để pha chế hai loại lít nước A và B là: \(45x + 15y \le 315.\)

Từ đó, ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,5x + 2y \le 12}\\{x + y \le 9}\\{45x + 15y \le 315}\end{array}.} \right.\)

Số điểm thưởng của đội chơi nhận được là: \(F\left( {x;y} \right) = 60x + 80y \to \max \)

• Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,5x + 2y \le 12}\\{x + y \le 9}\\{45x + 15y \le 315}\end{array}} \right.\)trên cùng mặt phẳng tọa độ \(Oxy.\)

Xác định miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ \(d:x = 0\) chứa điểm \(\left( {1;0} \right).\)

Xác định miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \({d_1}:y = 0\) chứa điểm \(\left( {0;1} \right).\)

Xác định miền nghiệm của bất phương trình \(0.5x + 2y \le 12\). Vẽ đường thẳng \({d_2}:0.5x + 2y = 12\) trên mặt phẳng tọa độ \(Oxy.\) Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(0,5x + 2y,\) ta được: \(0,5.0 + 2.0 = 0 < 12\) nên miền nghiệm của bất phương trình \(0.5x + 2y \le 12\) là nửa mặt phẳng bờ \({d_2}\) chứa điểm \(O\left( {0;0} \right)\).

Xác định miền nghiệm của bất phương trình \(x + y \le 9\). Vẽ đường thẳng \({d_3}:x + y = 9\) trên mặt phẳng tọa độ \(Oxy.\) Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_3}\) và thay vào biểu thức \(x + y,\) ta được: \(0 + 0 = 0 < 9\) nên miền nghiệm của bất phương trình  \(x + y = 9\) là nửa mặt phẳng bờ \({d_3}\) chứa điểm \(O\left( {0;0} \right)\).

Xác định miền nghiệm của bất phương trình \(45x + 15y \le 315\). Vẽ đường thẳng \({d_4}:45x + 15y = 315\) trên mặt phẳng tọa độ \(Oxy.\) Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_4}\) và thay vào biểu thức \(45x + 15y,\) ta được: \(45.0 + 15.0 = 0 < 315\) nên miền nghiệm của bất phương trình \(45x + 15y \le 315\) là nửa mặt phẳng bờ \({d_4}\) chứa điểm \(O\left( {0;0} \right)\).

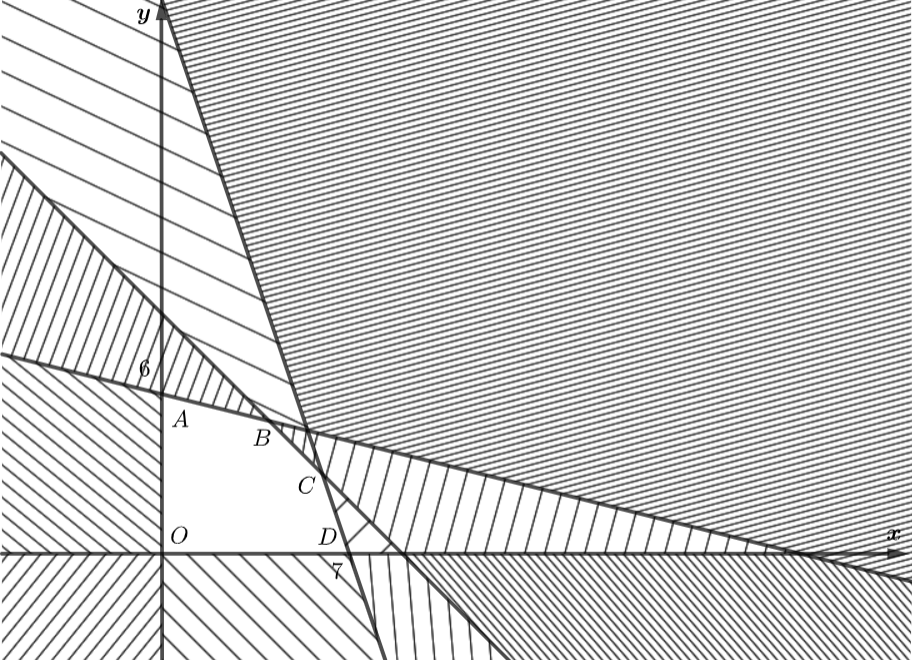
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,5x + 2y \le 12}\\{x + y \le 9}\\{45x + 15y \le 315}\end{array}} \right.\)là ngũ giác \(OABCD\) với \(A\left( {0;6} \right),\,\,B\left( {4;5} \right),\,\,C\left( {6;3} \right),\,\,D\left( {7;0} \right)\)

Ta có: \(F\left( {0;6} \right) = 60.0 + 80.6 = 480,\)

 \(F\left( {4;5} \right) = 60.4 + 80.5 = 640,\)

\(F\left( {0;0} \right) = 60.0 + 80.0 = 0,\)

\(F\left( {6;3} \right) = 60.6 + 80.3 = 600,\)

\(F\left( {7;0} \right) = 60.7 + 80.0 = 420.\)

\( \Rightarrow \) giá trị lớn nhất là \(F\left( {4;5} \right) = 640.\)

Vậy vần pha chế 4 lít nước loại A và 5 lít nước loại B thì số điểm thưởng nhận được là lớn nhất.