Giải bài 2.16 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức

Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.

Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Đề bài

Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.

Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây với chi phí là 80 nghìn đồng/giây. Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây với chi phí là 400 nghìn đồng/giây.

Công ty cần đặt thời gian quảng cáo trên các đài phát thanh và truyền hình như thế nào để hiệu quả nhất?

Gợi ý. Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài phát thanh và y (giây) trên truyền hình là F(x, y) = x + 8y. Ta cần tìm giá trị lớn nhất của hàm F(x, y) với x, y thoả mãn các điều kiện trong đề bài.

Phương pháp giải - Xem chi tiết

- Gọi x và y là số giây quảng cáo trên đài phát thanh và trên truyền hình.

- Dựa vào số tiền dự chi tối đa, thời lượng lập hệ bất phương trình tương ứng.

- Lập biểu thức F biểu diễn hiệu quả quảng cáo theo x và y.

- Tìm giá trị lớn nhất của hàm F(x;y) thỏa mãn các điều kiện trong đề bài.

Lời giải chi tiết

	Đài phát thanh	Truyền hình
Chi phí nhận quảng cáo	80 nghìn đồng /giây	400 nghìn đồng/giây
Hiệu quả quảng cáo	1 (đơn vị)	8 (đơn vị)

Gọi x và y là số giây quảng cáo trên đài phát thanh và trên truyền hình.

Khi đó \(x \ge 0;y \ge 0\)

160 triệu đồng=160000 (nghìn đồng)

Chi phí quảng cáo x giây trên đài phát thanh và y giây trên truyền hình là \(80x + 400y\)(nghìn đồng)

Vì công ty dự chi tối đa 160 triệu đồng nên ta có

\(80x + 400y \le 160000\)\( \Leftrightarrow x + 5y \le 2000\)

Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây nên ta có: \(x \le 900\)

Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây nên ta có: \(y \le 360\)

Ta có hệ bất phương trình:

\(\left\{ {\begin{array}{*{20}{l}}
{x \ge 0}\\
{y \ge 0}\\
{x + 5y \le 2000}\\
{x \le 900}\\
{y \le 360}
\end{array}} \right.\)

Xác định miền nghiệm là miền ngũ giác OABCD với:

A(900;0); B(900;220); C(200;360); D(0;360)

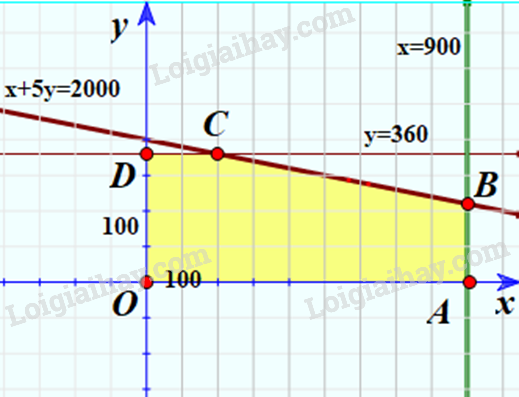
Hiệu quả quảng cáo là: \(F\left( {x;y} \right) = x + 8y\)

Ta có:

\(F\left( {0;0} \right) = 0\)

\(F\left( {900;0} \right) = 900 + 8.0 = 900\)

\(F\left( {900;220} \right) = 900 + 8.220 = 2660\)

\(F\left( {200;360} \right) = 3080\)

\(F\left( {0;360} \right) = 2880\)

Vậy công ty cần đặt thời gian quảng cáo trên đài phát thanh là 200 giây và trên truyền hình là 360 giây thì hiệu quả nhất.

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 14 phiếu

Giải bài 2.15 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm.
Giải bài 2.14 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ.
Giải bài 2.13 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ
Giải bài 2.12 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức
Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ.
Giải bài 2.11 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức
Cho hệ bất phương trình Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?
Giải bài 2.10 trang 31 SGK Toán 10 tập 1 – Kết nối tri thức
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Giải bài 2.9 trang 31 SGK Toán 10 tập 1 – Kết nối tri thức
Hình nào sau đây biểu diễn miền nghiệm của bất phương trình x - y < 3?
Giải bài 2.8 trang 31 SGK Toán 10 tập 1 – Kết nối tri thức
Cho bất phương trình 2x+y>3. Khẳng định nào sau đây là đúng?
Giải bài 2.7 trang 31 SGK Toán 10 tập 1 – Kết nối tri thức
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?