-
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
-
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Giải bài 1 trang 35 sách bài tập toán 10 - Chân trời sáng tạo
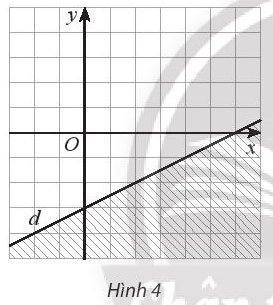
Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong hình 4 (mỗi ô vuông có cạnh là 1 đơn vị)
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong hình 4 (mỗi ô vuông có cạnh là 1 đơn vị)
Phương pháp giải - Xem chi tiết
Bước 1: Gọi phương trình tổng quát của đường thẳng bờ
Bước 2: Xác định các điểm đường thẳng đi qua và xác định phương trình
Bước 3: Thay tọa độ điểm O(0;0) là nghiệm của bất phương trình cần tìm và xác định dấu của bất phương trình
Lời giải chi tiết
Vì bờ của bất pương trình có dạng là đường thẳng tuyến tính nên phương trình tổng quát có dạng \(y = ax + b\)
Dựa vào hình 4 ta thấy đường thẳng đi qua điểm có tọa độ (6;0) và (0;3)
Thay tọa độ 2 điểm trên vào phương trình tổng quát ta có hệ phương trình hai ẩn như sau: \(\left\{ \begin{array}{l}0 = 6a + b\\3 = 0a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 3\end{array} \right.\)
Vậy phương trình bờ là \(y = - \frac{1}{2}x + 3 \Rightarrow F = \frac{1}{2}x + y - 3\)
Thay \(x = 0,y = 0\) vào phương trình trên ta có \(F = -3 < 0\)
Mặt khác ta thấy gốc tọa độ là nghiệm của bất phương trình (theo hình vẽ) và chứa cả bờ nên ta có bất phương trình cần tìm là \(\frac{1}{2}x + y - 3 \le 0\)
Bình luận
Chia sẻ
- Giải bài 2 trang 35 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 3 trang 35 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 4 trang 36 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 5 trang 36 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 6 trang 36 sách bài tập toán 10 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
