Đề ôn hè Toán 7 lên 8 - Đề 8

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Tập hợp các số vô tỉ được kí hiệu là

A. \(\mathbb{Z}\).

B. \(I\).

C. \(\mathbb{Q}\).

D. \(\mathbb{R}\).

Câu 2: Cách viết nào sau đây là đúng

A. \( - \left| { - 0,25} \right| = 0,25\).

B. \(\left| { - 0,25} \right| =  - 0,25\).

C. \(\left| { - 0,25} \right| = 0,25\).

D. \( - \left| { - 0,25} \right| =  - \left( { - 0,25} \right)\).

Câu 3: Số đối của số hữu tỉ \(\frac{{ - 3}}{5}\) là

A. \(\frac{5}{3}\).

B. \(\frac{3}{5}\).

C. \(\frac{5}{{ - 3}}\).

D. \(\frac{3}{{ - 5}}\).

Câu 4: Cho tam giác \(MNP\) có \(MN = MP\) và \(\widehat {NMP} = 70^\circ \). Số đo \(\widehat {MPN}\) bằng

A. \(140^\circ \).

B. \(110^\circ \).

C. \(70^\circ \).

D. \(55^\circ \).

Câu 5: Cho đoạn thẳng \(MN\), đường thẳng \(d\) là trung trực của \(MN\) thì:

A. \(d\) cắt đường thẳng \(MN\).

B. \(d\) đi qua trung điểm của \(MN\).

C. \(d\) đi qua trung điểm của \(MN\)và \(d \bot MN\).

D. \(d\) vuông góc với \(MN\).

Câu 6: Biểu đồ dưới đây thể hiện tỉ lệ các bạn học sinh khối 7 lựa chọn các môn học yêu thích. Em hãy cho biết môn học nào được các bạn học sinh lựa chọn nhiều nhất?

A. Tiếng Anh.

B. Văn.

C. KHTN.

D. Toán.

Câu 7: Cho biết đại lượng \(y\) tỉ lệ nghịch với đại lượng \(x\) theo hệ số tỉ lệ \(a\) và khi \(x = 2\) thì \(y =  - 5\). Khi đó hệ số \(a\) bằng

A. \(\frac{{ - 2}}{5}\).

B. \(\frac{{ - 5}}{2}\).

C. \(10\).

D. \( - 10\).

Câu 8: Giá trị của biểu thức \({y^2} - 2y - 1\) tại \(y =  - 3\) là

A. \(3\).

B. \(14\).

C. \( - 16\).

D. \( - 4\).

Câu 9: Trong tam giác \(ABC\), các đường cao \(AI\) và \(BJ\) cắt nhau tại \(H\) thì điểm \(H\)

A. là trọng tâm của \(\Delta ABC\).

B. cách đều ba đỉnh của \(\Delta ABC\).

C. là trực tâm của \(\Delta ABC\).

D. cách đều ba cạnh của \(\Delta ABC\).

Câu 10: Một thùng kín đựng \(10\) quả bóng màu xanh và \(10\) quả bóng màu đỏ có cùng hình dạng và kích thước. An lấy ngẫu nhiên một quả bóng trong thùng. Trong các biến cố sau, biến cố nào là biến cố chắc chắn?

A. A: “An lấy được quả bóng màu xanh”.

B. B: “An lấy được quả bóng màu đỏ”.

C. C: “An lấy được quả bóng màu xanh hoặc quả bóng màu đỏ”.

D. D: “An lấy được quả bóng màu vàng”.

Câu 11: Cho tam giác \(MNP\) có \(\widehat M = 52^\circ \); \(\widehat N = 58^\circ \). Khẳng định nào sau đây là đúng?

A. \(NP < MP < MN\).

B. \(MN < MP < NP\).

C. \(MP < MN < NP\).

D. \(NP < MN < MP\).

Câu 12: Một cuốn lịch để bàn có dạng hình lăng trụ đứng tam giác (như hình vẽ). Biết cuốn lịch có chiều cao bằng \(30\)\(cm\), đáy là tam giác cân có cạnh bên \(17\)\(cm\) và cạnh đáy bằng \(8\)\(cm\). Diện tích xung quanh của cuốn lịch là

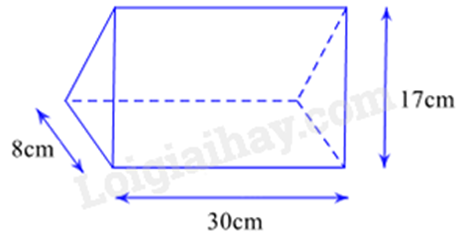
A. \(1260\)\(c{m^2}\).

B. \(990\)\(c{m^2}\).

C. \(1\)\(292\)\(c{m^2}\).

D. \(4\)\(080\)\(c{m^2}\).

Phần tự luận (7 điểm)

Bài 1. (2 điểm)

1) Thực hiện phép tính: \(\left| {\frac{{ - 1}}{2}} \right| + {\left( {\frac{{ - 1}}{3}} \right)^2}:\sqrt 4  + {\left( {\frac{2}{3}} \right)^2}\).

2) Tính \(\left( { - 3{x^2}} \right).\left( {\frac{1}{3}{x^3} + 2x - 4} \right)\).

3) Cho đa thức: \(P\left( x \right) = {x^5} - x + 5{x^2} - 2{x^5} + 4{x^3} - 7{x^2} + 3\).

a) Thu gọn và sắp xếp đa thức \(P\left( x \right)\) trên theo lũy thừa giảm dần của biến.

b) Xác định bậc, hệ số tự do, hệ số cao nhất của đa thức \(P\left( x \right)\).

Bài 2. (1 điểm) Một nhà hảo tâm tặng máy tính để bàn cho ba trường học ở một vùng khó khăn, nhằm giúp các em học sinh ở vùng đó có thêm cơ hội tiếp xúc với công nghệ thông tin. Biết rằng tổng số máy tính tặng là \(36\) máy và số máy tính được tặng của các trường tỉ lệ với \(2;3;4\). Tính số máy tính mà nhà hảo tâm đó tặng cho mỗi trường.

Bài 3. (1 điểm) Biểu đồ dưới đây cho biết số lượng các loại sách có trong thư viện của một trường học. Biết có \(775\) quyển sách giáo khoa trong thư viện.

a) Thư viện trường đó có tất cả bao nhiêu quyển sách?

b) Bạn Chi đến thư viện và chọn ngẫu nhiên một quyển sách trong số sách trên. Tính xác suất của biến cố “Quyển sách được chọn là sách khoa học hoặc sách truyện”.

Bài 4. (2,5 điểm)

1. Một hồ bơi dạng hình hộp chữ nhật có kích thước là chiều dài 12m, chiều rộng 5m và chiều sâu 3m (như hình vẽ). Tính thể tích nước khi bể bơi đầy nước.

2. Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến.

a) Chứng minh rằng: \(\Delta AMB = \Delta AMC\).

b) Gọi \(N\) là trung điểm của \(AC\). Trên tia đối của tia \(NB\) lấy điểm \(D\) sao cho \(NB = ND\). Chứng minh rằng \(AB{\rm{//}}DC\).

c) Trên tia đối của tia \(CA\) lấy điểm \(E\) sao cho \(CA = CE\). Gọi \(I\) là trung điểm của \(BE\). Chứng minh rằng \(C,D,I\) thẳng hàng.

Bài 5. (0,5 điểm) Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ đến bán kính \(100\)\(km\). Người ta đặt một trạm phát sóng 4G tại vị trí \(A\). Có một đảo nhỏ (tại vị trí \(B\)) chưa biết khoảng cách đến vị trí \(A\) nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí \(C\)) là \(70\)\(km\) và khách sạn đó cách trạm phát sóng là \(25\)\(km\)(như hình vẽ). Hỏi sóng 4G của trạm phát sóng tại vị trí \(A\) có thể phủ đến đảo đó được không? Vì sao?

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Tập hợp các số vô tỉ được kí hiệu là

A. \(\mathbb{Z}\).

B. \(I\).

C. \(\mathbb{Q}\).

D. \(\mathbb{R}\).

Phương pháp

Dựa vào kí hiệu các tập hợp.

Lời giải

Tập hợp số vô tỉ được kí hiệu là \(I\).

Đáp án: B.

Câu 2: Cách viết nào sau đây là đúng

A. \( - \left| { - 0,25} \right| = 0,25\).

B. \(\left| { - 0,25} \right| =  - 0,25\).

C. \(\left| { - 0,25} \right| = 0,25\).

D. \( - \left| { - 0,25} \right| =  - \left( { - 0,25} \right)\).

Phương pháp

\(\left| A \right|\) bằng \(A\) với \(A \ge 0\), bằng \( - A\) với \(A < 0\).

Lời giải

Ta có: \(\left| { - 0,25} \right| = 0,25\), \( - \left| { - 0,25} \right| =  - 0,25\) nến C đúng.

Đáp án: C.

Câu 3: Số đối của số hữu tỉ \(\frac{{ - 3}}{5}\) là

A. \(\frac{5}{3}\).

B. \(\frac{3}{5}\).

C. \(\frac{5}{{ - 3}}\).

D. \(\frac{3}{{ - 5}}\).

Phương pháp

Hai số đối nhau nếu tổng của chúng bằng 0.

Lời giải

Số đối của số hữu tỉ \(\frac{{ - 3}}{5}\) là: \(0 - \frac{{ - 3}}{5} = \frac{3}{5}\).

Đáp án: B.

Câu 4: Cho tam giác \(MNP\) có \(MN = MP\) và \(\widehat {NMP} = 70^\circ \). Số đo \(\widehat {MPN}\) bằng

A. \(140^\circ \).

B. \(110^\circ \).

C. \(70^\circ \).

D. \(55^\circ \).

Phương pháp

Chứng minh tam giác MNP cân tại M, suy ra hai góc ở đáy bằng nhau.

Áp dụng định lí tổng ba góc trong tam giác bằng \(180^\circ \) vào tam giác MNP để tính góc MPN.

Lời giải

Vì MN = MP nên tam giác MNP cân tại M, suy ra \(\widehat {MNP} = \widehat {MPN}\).

Áp dụng định lí tổng ba góc trong tam giác MNP, ta có:

\(\widehat {NMP} + \widehat {MNP} + \widehat {MPN} = 180^\circ \)

\(\widehat {NMP} + 2\widehat {MPN} = 180^\circ \)

suy ra \(2\widehat {MPN} = 180^\circ  - \widehat {NMP} = 180^\circ  - 70^\circ  = 110^\circ \).

Suy ra \(\widehat {MPN} = 110^\circ :2 = 55^\circ \).

Đáp án: D.

Câu 5: Cho đoạn thẳng \(MN\), đường thẳng \(d\) là trung trực của \(MN\) thì:

A. \(d\) cắt đường thẳng \(MN\).

B. \(d\) đi qua trung điểm của \(MN\).

C. \(d\) đi qua trung điểm của \(MN\) và \(d \bot MN\).

D. \(d\) vuông góc với \(MN\).

Phương pháp

Đường trung trực của đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của đoạn thẳng.

Lời giải

Đường thẳng \(d\) là trung trực của \(MN\) thì \(d\) đi qua trung điểm của \(MN\) và \(d \bot MN\).

Đáp án: C.

Câu 6: Biểu đồ dưới đây thể hiện tỉ lệ các bạn học sinh khối 7 lựa chọn các môn học yêu thích. Em hãy cho biết môn học nào được các bạn học sinh lựa chọn nhiều nhất?

A. Tiếng Anh.

B. Văn.

C. KHTN.

D. Toán.

Phương pháp

So sánh các tỉ số phần trăm với nhau.

Môn chiếm tỉ số phần trăm lớn nhất là môn học được các bạn học sinh lựa chọn nhiều nhất.

Lời giải

Vì 37,5% > 25,0% > 17,5% > 20,0% nên môn Toán là môn học được các bạn học sinh lựa chọn nhiều nhất.

Đáp án: D.

Câu 7: Cho biết đại lượng \(y\) tỉ lệ nghịch với đại lượng \(x\) theo hệ số tỉ lệ \(a\) và khi \(x = 2\) thì \(y =  - 5\). Khi đó hệ số \(a\) bằng

A. \(\frac{{ - 2}}{5}\).

B. \(\frac{{ - 5}}{2}\).

C. \(10\).

D. \( - 10\).

Phương pháp

Đại lượng \(y\) tỉ lệ nghịch với đại lượng \(x\) theo hệ số tỉ lệ \(a\) thì \(xy = a\).

Lời giải

Hệ số tỉ lệ a là: \(x.y = 2.\left( { - 5} \right) =  - 10\).

Đáp án: D.

Câu 8: Giá trị của biểu thức \({y^2} - 2y - 1\) tại \(y =  - 3\) là

A. \(3\).

B. \(14\).

C. \( - 16\).

D. \( - 4\).

Phương pháp

Thay \(y =  - 3\) vào biểu thức để tính giá trị.

Lời giải

Giá trị của biểu thức \({y^2} - 2y - 1\) tại \(y =  - 3\) là:

\({\left( { - 3} \right)^2} - 2.\left( { - 3} \right) - 1 = 14\).

Đáp án: B.

Câu 9: Trong tam giác \(ABC\), các đường cao \(AI\) và \(BJ\) cắt nhau tại \(H\) thì điểm \(H\)

A. là trọng tâm của \(\Delta ABC\).

B. cách đều ba đỉnh của \(\Delta ABC\).

C. là trực tâm của \(\Delta ABC\).

D. cách đều ba cạnh của \(\Delta ABC\).

Phương pháp

Dựa vào tính chất giao điểm của các đường đặc biệt trong tam giác.

Lời giải

Vì các đường cao \(AI\) và \(BJ\) cắt nhau tại \(H\) nên H là trực tâm của tam giác ABC.

Đáp án: C.

Câu 10: Một thùng kín đựng \(10\) quả bóng màu xanh và \(10\) quả bóng màu đỏ có cùng hình dạng và kích thước. An lấy ngẫu nhiên một quả bóng trong thùng. Trong các biến cố sau, biến cố nào là biến cố chắc chắn?

A. A: “An lấy được quả bóng màu xanh”.

B. B: “An lấy được quả bóng màu đỏ”.

C. C: “An lấy được quả bóng màu xanh hoặc quả bóng màu đỏ”.

D. D: “An lấy được quả bóng màu vàng”.

Phương pháp

Biến cố chắc chắn là biến cố biết trước được luôn xảy ra.

Lời giải

Biến cố A: “An lấy được quả bóng màu xanh” là biến cố ngẫu nhiên vì trong thùng có bóng màu xanh và bóng màu đỏ nên quả bóng lấy ra có thể là màu xanh hoặc màu đỏ.

Biến cố B: “An lấy được quả bóng màu đỏ” là biến cố ngẫu nhiên vì trong thùng có bóng màu xanh và bóng màu đỏ nên quả bóng lấy ra có thể là màu xanh hoặc màu đỏ.

Biến cố C: “An lấy được quả bóng màu xanh hoặc quả bóng màu đỏ” là biến cố chắc chắn vì trong thùng có bóng màu xanh và bóng màu đỏ nên quả bóng lấy ra có thể là màu xanh hoặc màu đỏ.

Biến cố D: “An lấy được quả bóng màu vàng” là biến cố không thể vì trong thùng không có bóng màu vàng.

Đáp án: C.

Câu 11: Cho tam giác \(MNP\) có \(\widehat M = 52^\circ \); \(\widehat N = 58^\circ \). Khẳng định nào sau đây là đúng?

A. \(NP < MP < MN\).

B. \(MN < MP < NP\).

C. \(MP < MN < NP\).

D. \(NP < MN < MP\).

Phương pháp

Áp dụng định lí tổng ba góc trong tam giác bằng \(180^\circ \) để tính \(\widehat P\).

So sánh các cạnh dựa vào số đo các góc đối diện cạnh đó.

Lời giải

Áp dụng định lí tổng ba góc vào tam giác MNP, ta có:

\(\widehat M + \widehat N + \widehat P = 180^\circ \).

\(52^\circ  + 58^\circ  + \widehat P = 180^\circ \)

Suy ra \(\widehat P = 180^\circ  - 52^\circ  - 58^\circ  = 70^\circ \).

Vì \(\widehat M < \widehat N < \widehat P\left( {52^\circ  < 58^\circ  < 70^\circ } \right)\) nên \(NP < MP < MN\). \(\)

Đáp án: A.

Câu 12: Một cuốn lịch để bàn có dạng hình lăng trụ đứng tam giác (như hình vẽ). Biết cuốn lịch có chiều cao bằng \(30\)\(cm\), đáy là tam giác cân có cạnh bên \(17\)\(cm\) và cạnh đáy bằng \(8\)\(cm\). Diện tích xung quanh của cuốn lịch là

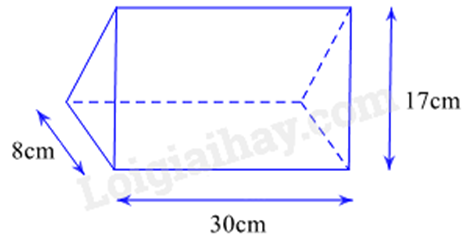
A. \(1260\)\(c{m^2}\).

B. \(990\)\(c{m^2}\).

C. \(1\)\(292\)\(c{m^2}\).

D. \(4\)\(080\)\(c{m^2}\).

Phương pháp

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân chiều cao.

Lời giải

Diện tích xung quanh của cuốn lịch là:

C_đáy.h \( = \left( {8 + 17.2} \right).30 = 1260\left( {c{m^2}} \right)\)

Đáp án: A.

Phần tự luận.

Bài 1. (2 điểm)

1) Thực hiện phép tính: \(\left| {\frac{{ - 1}}{2}} \right| + {\left( {\frac{{ - 1}}{3}} \right)^2}:\sqrt 4  + {\left( {\frac{2}{3}} \right)^2}\).

2) Tính \(\left( { - 3{x^2}} \right).\left( {\frac{1}{3}{x^3} + 2x - 4} \right)\).

3) Cho đa thức: \(P\left( x \right) = {x^5} - x + 5{x^2} - 2{x^5} + 4{x^3} - 7{x^2} + 3\).

a) Thu gọn và sắp xếp đa thức \(P\left( x \right)\) trên theo lũy thừa giảm dần của biến.

b) Xác định bậc, hệ số tự do, hệ số cao nhất của đa thức \(P\left( x \right)\).

Phương pháp

1) Sử dụng kiến thức về phép tính với số thực, căn bậc hai, giá trị tuyệt đối của một số, luỹ thừa với số mũ tự nhiên.

2) Thực hiện nhân đơn thức với đa thức, ta nhân đơn thức với từng đơn thức của đa thức để tính.

3)

a) Nhóm các hạng tử có cùng số mũ với nhau, thực hiện cộng trừ để thu gọn đa thức.

b) Bậc của đa thức là bậc của hạng tử có số mũ lớn nhất.

Hệ số tự do là hệ số không chứa ẩn.

Hệ số cao nhất là hệ số của hạng tử có số mũ lớn nhất.

Lời giải

1) \(\left| {\frac{{ - 1}}{2}} \right| + {\left( {\frac{{ - 1}}{3}} \right)^2}:\sqrt 4  + {\left( {\frac{2}{3}} \right)^2}\)

\( = \frac{1}{2} + \frac{1}{9}:2 + \frac{4}{9}\)

\( = \frac{1}{2} + \frac{1}{{18}} + \frac{4}{9}\)

\( = \frac{9}{{18}} + \frac{1}{{18}} + \frac{8}{{18}}\)

\( = \frac{{18}}{{18}} = 1\)

2) \(\left( { - 3{x^2}} \right).\left( {\frac{1}{3}{x^3} + 2x - 4} \right)\)

\( = \left( { - 3{x^2}} \right).\left( {\frac{1}{3}{x^3}} \right) + \left( { - 3{x^2}} \right).\left( {2x} \right) + \left( { - 3{x^2}} \right).\left( { - 4} \right)\)

\( =  - {x^5} - 6{x^3} + 12{x^2}\).

3)

a) \(P\left( x \right) = {x^5} - x + 5{x^2} - 2{x^5} + 4{x^3} - 7{x^2} + 3\)

         \(\begin{array}{l} = \left( {{x^5} - 2{x^5}} \right) + 4{x^3} + \left( {5{x^2} - 7{x^2}} \right) - x + 3\\ =  - {x^5} + 4{x^3} - 2{x^2} - x + 3\end{array}\)

Đa thức \(P\left( x \right)\) sắp xếp theo lũy thừa giảm dần của biến là: \(P\left( x \right) =  - {x^5} + 4{x^3} - 2{x^2} - x + 3\).

b) Đa thức \(P\left( x \right)\) có:

+ Bậc là \(5\).

+ Hệ số tự do là \(3\).

+ Hệ số cao nhất là \( - 1\).

Bài 2. (1 điểm) Một nhà hảo tâm tặng máy tính để bàn cho ba trường học ở một vùng khó khăn, nhằm giúp các em học sinh ở vùng đó có thêm cơ hội tiếp xúc với công nghệ thông tin. Biết rằng tổng số máy tính tặng là \(36\) máy và số máy tính được tặng của các trường tỉ lệ với \(2;3;4\). Tính số máy tính mà nhà hảo tâm đó tặng cho mỗi trường.

Phương pháp

Gọi số máy tính nhà hảo tâm tặng cho trường thứ nhất, trường thứ hai và trường thứ ba lần lượt là \(x,y,z\) (máy) (điều kiện \(x,y,z \in {\mathbb{N}^*}\))

Theo bài ra ta có: \(x + y + z = 36\); \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\).

Áp dụng tính chất của dãy tỉ số bằng nhau để tìm \(x,y,z\).

Lời giải

Gọi số máy tính nhà hảo tâm tặng cho trường thứ nhất, trường thứ hai và trường thứ ba lần lượt là \(x,y,z\) (máy) (điều kiện \(x,y,z \in {\mathbb{N}^*}\))

Theo bài ra, ta có tổng số máy tính tặng là \(36\) máy nên \(x + y + z = 36\)

Số máy tính được tặng của các trường tỉ lệ với \(2;3;4\) nên \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{{x + y + z}}{{2 + 3 + 4}} = \frac{{36}}{9} = 4\)

+)  \(\frac{x}{2} = 4\) suy ra \(x = 4.2 = 8\).

+) \(\frac{y}{3} = 4\) suy ra \(y = 4.3 = 12\)

+) \(\frac{z}{4} = 4\) suy ra \(x = 4.4 = 16\)

Vậy số máy tính nhà hảo tâm tặng trường thứ nhất, trường thứ hai, trường thứ ba lần lượt là \(8\) máy, \(12\) máy, \(16\) máy.

Bài 3. (1 điểm) Biểu đồ dưới đây cho biết số lượng các loại sách có trong thư viện của một trường học. Biết có \(775\) quyển sách giáo khoa trong thư viện.

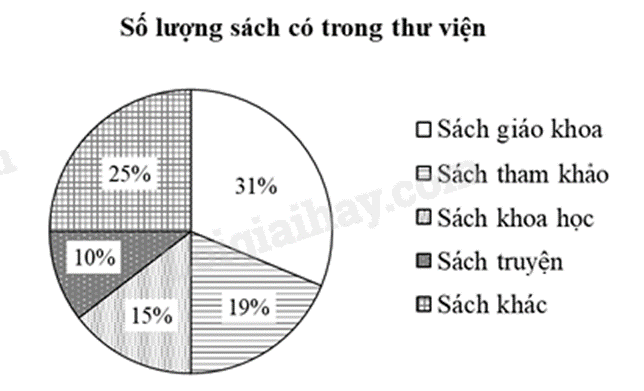
a) Thư viện trường đó có tất cả bao nhiêu quyển sách?

b) Bạn Chi đến thư viện và chọn ngẫu nhiên một quyển sách trong số sách trên. Tính xác suất của biến cố “Quyển sách được chọn là sách khoa học hoặc sách truyện”.

Phương pháp

a) Dựa vào số quyển sách giáo khoa ứng với 31% để tính tổng số quyển sách trong thư viện.

b) Xác định số quyển sách khoa học, sách truyện trong thư viện: số quyển sách ứng với tỉ số phần trăm của tổng số quyển sách trong thư viện.

Xác suất của biến cố bằng tỉ số giữa số quyển sách khoa học và sách truyện với tổng số sách.

Lưu ý: Kết quả thuận lợi của biến cố “Quyển sách được chọn là sách khoa học hoặc sách truyện” là tổng số quyển sách giáo khoa và sách truyện.

Lời giải

a) Thư viện trường đó có số sách là: \(775:31\%  = 2500\) (quyển)

b) Số quyển sách khoa học có trong thư viện là: \(2500.15\%  = 375\) (quyển)

Số quyển sách truyện có trong thư viện là: \(2500.10\%  = 250\) (quyển)

Số quyển sách khoa học và sách truyện có trong thư viện là:

\(375 + 250 = 625\) (quyển)

Xác suất của biến cố “Quyển sách được chọn là sách khoa học hoặc sách truyện” là: \(625:2500 = \frac{1}{4}\).

Bài 4. (2,5 điểm)

1. Một hồ bơi dạng hình hộp chữ nhật có kích thước là chiều dài 12m, chiều rộng 5m và chiều sâu 3m. Tính thể tích nước khi bể bơi đầy nước.

2. Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến.

a) Chứng minh rằng: \(\Delta AMB = \Delta AMC\).

b) Gọi \(N\) là trung điểm của \(AC\). Trên tia đối của tia \(NB\) lấy điểm \(D\) sao cho \(NB = ND\). Chứng minh rằng \(AB{\rm{//}}DC\).

c) Trên tia đối của tia \(CA\) lấy điểm \(E\) sao cho \(CA = CE\). Gọi \(I\) là trung điểm của \(BE\). Chứng minh rằng \(C,D,I\) thẳng hàng.

Phương pháp

1. Thể tích nước khi đầy bể chính là thể tích của hình hộp chữ nhật.

Thể tích hình hộp chữ nhật = chiều dài.chiều rộng.chiều cao.

2. a) Dựa vào tính chất của tam giác cân và đường trung tuyến để chứng minh \(\Delta AMB = \Delta AMC\left( {c.c.c} \right)\)

b) Chứng minh \(\Delta ANB = \Delta CND\left( {c.g.c} \right)\) nên \(\widehat {BAN} = \widehat {DCN}\) (hai góc tương ứng)

Hai góc ở vị trí so le trong bằng nhau thì \(AB{\rm{//}}DC\).

c) Chứng minh EN là đường trung tuyến của \(\Delta BDE\).

Chứng minh \(C \in NE\) và \(CE = \frac{2}{3}EN\) suy ra \(C\) là trọng tâm của \(\Delta BDE\).

Chứng minh DI là đường trung tuyến của \(\Delta BDE\) nên D, C, I thẳng hàng.

Lời giải

1.

Thể tích nước khi bể bơi đầy nước là: \(12.5.3 = 180\left( {{m^3}} \right)\).

Vậy thể tích nước khi bể bơi đầy nước là \(180{m^3}\).

2.

a) Ta có tam giác \(\Delta ABC\) cân tại \(A\) (gt) nên \(AB = AC\)

Vì AM là đường trung tuyến của \(\Delta ABC\) (gt) nên \(MB = MC\)

Xét \(\Delta AMB\) và \(\Delta AMC\) có

\(\begin{array}{l}AB = AC\left( {cmt} \right)\\MB = MC\left( {cmt} \right)\end{array}\)

AM là cạnh chung

Vậy \(\Delta AMB = \Delta AMC\left( {c.c.c} \right)\)

b) Vì \(N\) là trung điểm của AC (gt) nên \(NA = NC\)

Xét \(\Delta ANB\) và \(\Delta CND\) có

\(NA = NC\left( {cmt} \right)\)

\(\widehat {ANB} = \widehat {CND}\) (hai góc đối đỉnh)

\(NB = ND\left( {gt} \right)\)

suy ra \(\Delta ANB = \Delta CND\left( {c.g.c} \right)\)

nên \(\widehat {BAN} = \widehat {DCN}\) (hai góc tương ứng)

mà hai góc này ở vị trí so le trong.

Vậy \(AB{\rm{//}}DC\).

c) Ta có \(AC = EC\left( {gt} \right)\)

Mà \(CN = NA = \frac{1}{2}AC\left( {gt} \right)\) nên \(CN = \frac{1}{2}EC\left( {gt} \right)\)

Suy ra \(CE = 2CN = 2.\frac{1}{3}EN = \frac{2}{3}EN\)

Xét \(\Delta BDE\) có \(N\) là trung điểm của BD nên EN là đường trung tuyến của \(\Delta BDE\).

Mà \(C \in NE\) và \(CE = \frac{2}{3}EN\).

Suy ra \(C\) là trọng tâm của \(\Delta BDE\).

Lại có DI là đường trung tuyến của \(\Delta BDE\).

Vậy D, C, I thẳng hàng.

Bài 5. (0,5 điểm) Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ đến bán kính \(100\)\(km\). Người ta đặt một trạm phát sóng 4G tại vị trí \(A\). Có một đảo nhỏ (tại vị trí \(B\)) chưa biết khoảng cách đến vị trí \(A\) nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí \(C\)) là \(70\)\(km\) và khách sạn đó cách trạm phát sóng là \(25\)\(km\)(như hình vẽ). Hỏi sóng 4G của trạm phát sóng tại vị trí \(A\) có thể phủ đến đảo đó được không? Vì sao?

Phương pháp

Xác định độ dài các cạnh của tam giác ABC đã có ở đề bài.

Theo bất đẳng thức tam giác ta có: \(AB < AC + BC\)

Thay số để suy ra độ dài tối đa của AB.

So sánh với bán kính sóng 4G có thể phủ đến và kết luận.

Lời giải

Quan sát hình vẽ ta thấy ba vị trí \(A,B,C\) tạo thành ba đỉnh của tam giác \(ABC\) với \(AC = 25\,km\), \(BC = 70\,km\).

Theo bất đẳng thức tam giác ta có: \(AB < AC + BC\)

hay \(AB < 25 + 70\)

suy ra \(AB < 95 < 100\)

Mà sóng 4G có thể phủ đến bán kính \(100\,km\)

Vậy sóng 4G của trạm phát sóng tại vị trí \(A\) có thể phủ đến đảo nhỏ tại vị trí \(B\).