Đề ôn hè Toán 7 lên 8 - Đề 1

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Phát biểu nào sau đây là đúng?

A. \(\pi  \in \mathbb{N}\).

B. \(3,(5) \in \mathbb{Q}\).

C. \( - 13 \notin \mathbb{R}\).

D. \(0 \in I\).

Câu 2: Căn bậc hai số học của 121 là

A. -11.

B. 11.

C. 60,5.

D. – 60,5.

Câu 3: Oz là tia phân giác của \(\widehat {xOy}\) khi:

A. \(\widehat {xOz} = \widehat {zOy} = \widehat {xOy}\).

B. \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2}\).

C. \(\widehat {xOz} = \frac{{\widehat {xOy}}}{2}\).

D. \(\widehat {xOz} = \widehat {zOy} = 2.\widehat {xOy}\).

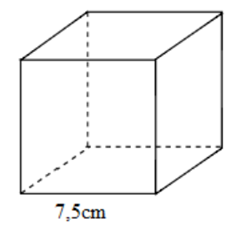
Câu 4: Thể tích của hình lập phương (hình bên) là bao nhiêu?

A. \(421c{m^3}\).

B. \(421,587c{m^3}\).

C. \(421,875c{m^3}\).

D. \(421,785c{m^3}\).

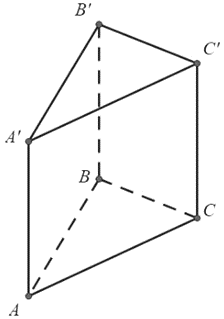
Câu 5: Cho hình lăng trụ đứng tam giác như hình bên. Mặt đáy của hình lăng trụ đứng là:

A. BB’C’C.

B. ABC.

C. A’B’BA.

D. A’C’CA.

Câu 6: Cho \(\Delta ABC = \Delta DEF\). Khi đó:

A. AB = ED.

B. AC = DE.

C. BC = DF.

D. BC = DE.

Câu 7: Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn môn học yêu thích nhất trong 4 môn: Toán học, Văn học, Thể dục, Âm nhạc của học sinh khối 7 ở trường B.

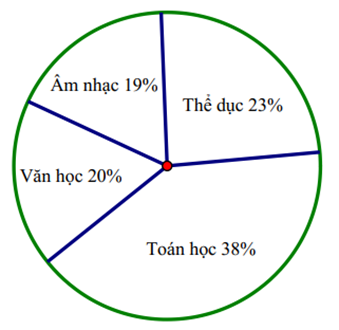
Mỗi học sinh chỉ được chọn 1 môn khi được hỏi ý kiến. Hỏi tổng số học sinh chọn môn Âm nhạc và Thể dục chiếm bao nhiêu phần trăm?

A. 19%.

B. 42%.

C. 39%.

D. 43%.

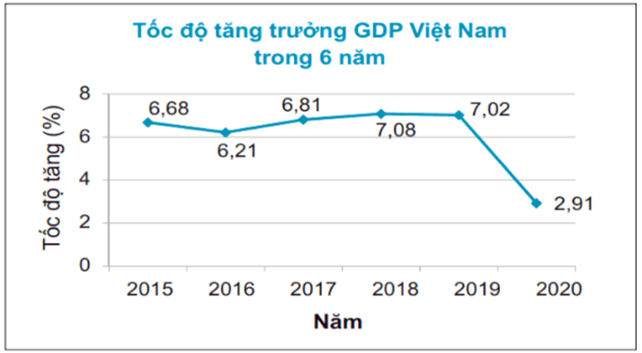
Câu 8: Biểu đồ đoạn thẳng trong hình bên biểu diễn tốc độ tăng trưởng GDP Việt Nam trong 6 năm 2015, 2016, 2017, 2018, 2019, 2020. Hãy cho biết tốc độ tăng trưởng GDP năm nào là cao nhất?

A. 2019.

B. 2020.

C. 2018.

D. 2016.

Câu 9: Gieo một con xúc xắc cân đối có 6 mặt. Xác suất của biến cố A: “Số chấm xuất hiện trên mặt con xúc xắc là 6” là:

A. \(\frac{1}{2}\).

B. \(\frac{1}{3}\).

C. \(\frac{1}{6}\).

D. 1.

Câu 10: Giá tiền của 6 quyển vở là bao nhiêu biết rằng 4 quyển vở giá 36 000 đồng?

A. 24 000 đồng.

B. 54 000 đồng.

C. 65 000 đồng.

D. 85 000 đồng.

Câu 11: Biểu thức đại số nào sau đây biểu thị chu vi hình chữ nhật có chiều rộng bằng 8(cm) và chiều dài bằng x (cm)?

A. \(8 + x\).

B. \((8 + x).2\).

C. \(8.x\).

D. \(\left( {8.x} \right).2\).

Câu 12: Cho hình vẽ bên, với \(G\) là trọng tâm của \(\Delta ABC.\) Điền số thích hợp vào chỗ chấm: \(BE = ....GE\).

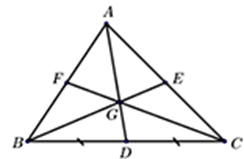
A. \(\frac{2}{3}\).

B. 2.

C. \(\frac{1}{2}\).

D. 3.

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm)

a) Tính: \(\sqrt {\frac{{25}}{{16}}} .1,5 + {\left( {0,25} \right)^2}:\left| { - \frac{1}{4}} \right| - {\left( {\frac{{2023}}{{2024}}} \right)^0}\).

b) Tìm x, biết:

i. \(\frac{3}{4}x - \frac{1}{2} = 20\% \).

ii. \(\left| {x + \frac{3}{4}} \right| - \frac{2}{5} = 1\).

Bài 2. (1,5 điểm)

a) Một nhà thầu ước tính rằng có thể hoàn thành một hợp đồng xây dựng trong 12 tháng với 280 công nhân. Nếu được yêu cầu phải hoàn hoàn thành hợp đồng trong 10 tháng thì nhà thầu đó phải thuê bao nhiêu công nhân (biết năng suất lao động của mỗi công nhân là như nhau)?

b) Chứng minh giá trị của đa thức \(f\left( x \right) = x\left( {1 - 2x} \right) + \left( {2{x^2} - x + 4} \right)\) không phụ thuộc vào \(x\).

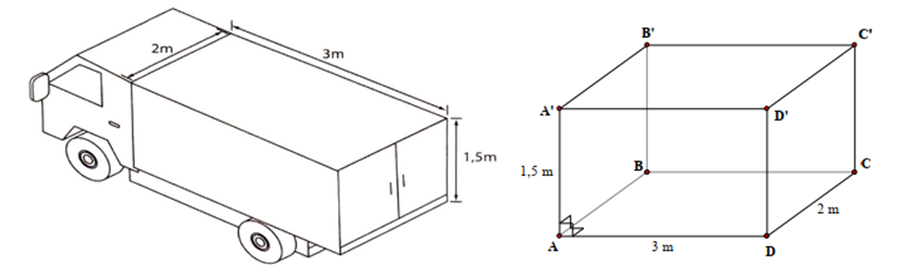
Bài 3. (1 điểm) Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên. Tính thể tích của thùng xe và diện tích phần Inox đóng thùng xe (tính luôn sàn).

Bài 4. (2,5 điểm) Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Vẽ AD vuông góc với BC (\(D \in BC\)).

a) Tính số đo các góc còn lại của tam giác ABC.

b) Chứng minh: \(\Delta ADB = \Delta ADC\).

c) Gọi M là trung điểm của DB. Từ M vẽ đường thẳng vuông góc với BC cắt AB tại E. Chứng minh:  DE // AC.

Bài 5. (0,5 điểm) Có một chi tiết máy (đường viền ngoài là đường tròn) bị gãy (hình vẽ). Làm thế nào xác định được bán kính của đường viền này.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Phát biểu nào sau đây là đúng?

A. \(\pi  \in \mathbb{N}\).

B. \(3,(5) \in \mathbb{Q}\).

C. \( - 13 \notin \mathbb{R}\).

D. \(0 \in I\).

Phương pháp

Dựa vào kiến thức về tập số tự nhiên, số hữu tỉ, số thực, số vô tỉ.

Lời giải

\(\pi  \approx 3,14 \notin \mathbb{N}\) nên A sai.

\(3,(5) = \frac{{32}}{9} \in \mathbb{Q}\) nên B đúng.

\( - 13 \in \mathbb{R}\) nên C sai.

\(0 \in \mathbb{Q}\) nên \(0 \notin I\) nên D sai.

Đáp án: B.

Câu 2: Căn bậc hai số học của 121 là

A. -11.

B. 11.

C. 60,5.

D. – 60,5.

Phương pháp

Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \), là số x không âm sao cho \({x^2} = a\).

Lời giải

\(\sqrt {121}  = 11\) vì 11 > 0 và \({11^2} = 121\).

Đáp án: B.

Câu 3: Oz là tia phân giác của \(\widehat {xOy}\) khi:

A. \(\widehat {xOz} = \widehat {zOy} = \widehat {xOy}\).

B. \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2}\).

C. \(\widehat {xOz} = \frac{{\widehat {xOy}}}{2}\).

D. \(\widehat {xOz} = \widehat {zOy} = 2.\widehat {xOy}\).

Phương pháp

Tia phân giác của một góc chia góc đó thành hai góc bằng nhau và bằng một nửa số đo góc ấy.

Lời giải

Vì Oz là tia phân giác của \(\widehat {xOy}\)  nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}\widehat {xOy}\).

Đáp án: B.

Câu 4: Thể tích của hình lập phương (hình bên) là bao nhiêu?

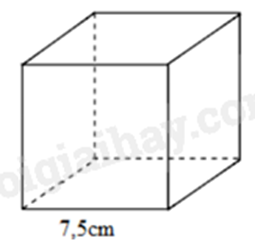
A. \(421c{m^3}\).

B. \(421,587c{m^3}\).

C. \(421,875c{m^3}\).

D. \(421,785c{m^3}\).

Phương pháp

Thể tích của hình lập phương cạnh a là \(V = a.a.a\).

Lời giải

Thể tích hình lập phương là: \(7,5.7,5.7,5 = 421,875\left( {c{m^3}} \right)\).

Đáp án: C.

Câu 5: Cho hình lăng trụ đứng tam giác như hình bên. Mặt đáy của hình lăng trụ đứng là:

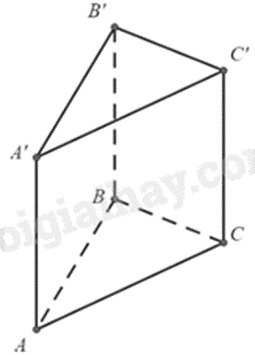
A. BB’C’C.

B. ABC.

C. A’B’BA.

D. A’C’CA.

Phương pháp

Hình lăng trụ đứng tam giác có đáy là hình tam giác.

Lời giải

Mặt đáy của hình lăng trụ đứng trên là mặt ABC, A’B’C’ nên ta chọn đáp án B.

Đáp án: B.

Câu 6: Cho \(\Delta ABC = \Delta DEF\). Khi đó:

A. AB = ED.

B. AC = DE.

C. BC = DF.

D. BC = DE.

Phương pháp

Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.

Lời giải

Vì \(\Delta ABC = \Delta DEF\) nên AB = DE, AC = DF, BC = EF nên A đúng.

Đáp án: A.

Câu 7: Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn môn học yêu thích nhất trong 4 môn: Toán học, Văn học, Thể dục, Âm nhạc của học sinh khối 7 ở trường B.

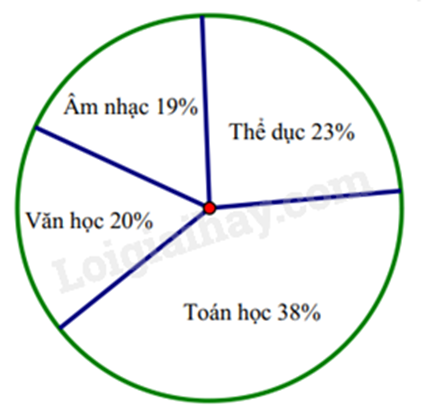
Mỗi học sinh chỉ được chọn 1 môn khi được hỏi ý kiến. Hỏi tổng số học sinh chọn môn Âm nhạc và Thể dục chiếm bao nhiêu phần trăm?

A. 19%.

B. 42%.

C. 39%.

D. 43%.

Phương pháp

Tính tổng số phần trăm của môn Âm nhạc và Thể dục.

Lời giải

Quan sát biểu đồ ta thấy tổng số học sinh chọn môn Âm nhạc và Thể dục chiếm số phần trăm là:

\(19\%  + 23\%  = 42\% \).

Đáp án: B.

Câu 8: Biểu đồ đoạn thẳng trong hình bên biểu diễn tốc độ tăng trưởng GDP Việt Nam trong 6 năm 2015, 2016, 2017, 2018, 2019, 2020. Hãy cho biết tốc độ tăng trưởng GDP năm nào là cao nhất?

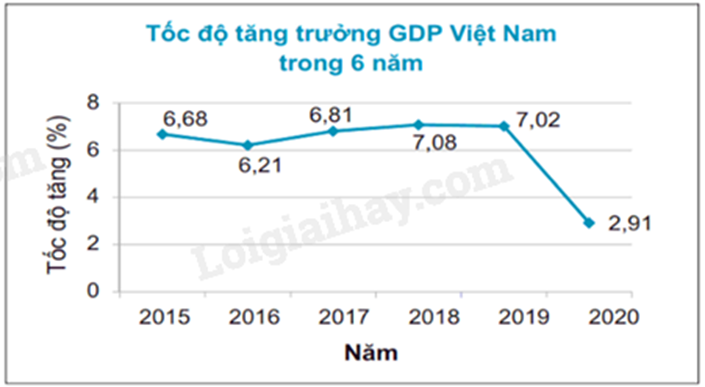
A. 2019.

B. 2020.

C. 2018.

D. 2016.

Phương pháp

Quan sát biểu đồ xác định số lớn nhất ứng với năm có tốc độ tăng trưởng GDP cao nhất.

Lời giải

Vì 7,08 là số lớn nhất, ứng với năm 2018 nên tốc độ tăng trưởng GDP năm 2018 là cao nhất.

Đáp án: C.

Câu 9: Gieo một con xúc xắc cân đối có 6 mặt. Xác suất của biến cố A: “Số chấm xuất hiện trên mặt con xúc xắc là 6” là:

A. \(\frac{1}{2}\).

B. \(\frac{1}{3}\).

C. \(\frac{1}{6}\).

D. 1.

Phương pháp

Xúc xắc cân đối nên khả năng xuất hiện của các mặt là như nhau nên ta tính được xác suất xuất hiện của mỗi mặt.

Suy ra xác suất của biến cố A.

Lời giải

Khi gieo một con xúc xắc cân đối thì 6 mặt của nó có khả năng xuất hiện bằng nhau nên xác suất xuất hiện của mỗi mặt đều là \(\frac{1}{6}\).

Do 6 kết quả đều có khả năng xảy ra bằng nhau nên P(A) = \(\frac{1}{6}\).

Đáp án: C.

Câu 10: Giá tiền của 6 quyển vở là bao nhiêu biết rằng 4 quyển vở giá 36 000 đồng?

A. 24 000 đồng.

B. 54 000 đồng.

C. 65 000 đồng.

D. 85 000 đồng.

Phương pháp

Gọi x (đồng) là giá tiền của 6 quyển vở.

Vì số quyển vở và giá tiền tỉ lệ thuận nên áp dụng tính chất của hai đại lượng tỉ lệ thuận để tìm x.

Lời giải

Gọi x (đồng) là giá tiền của 6 quyển vở.

Vì số quyển vở và giá tiền tỉ lệ thuận nên theo tính chất của hai đại lượng tỉ lệ thuận ta có:

\(\frac{4}{6} = \frac{{36000}}{x}\)

Suy ra \(x = \frac{{6.36000}}{4} = 54000\).

Vậy giá tiền 6 quyển vở là 54 000 đồng.

Đáp án: B.

Câu 11: Biểu thức đại số nào sau đây biểu thị chu vi hình chữ nhật có chiều rộng bằng 8(cm) và chiều dài bằng x (cm)?

A. \(8 + x\).

B. \((8 + x).2\).

C. \(8.x\).

D. \(\left( {8.x} \right).2\).

Phương pháp

Sử dụng công thức tính chu vi hình chữ nhật = (chiều rộng + chiều dài).2 để biểu diễn.

Lời giải

Biểu thức biểu thị chu vi hình chữ nhật là: \(\left( {8 + x} \right).2\).

Đáp án: B.

Câu 12: Cho hình vẽ bên, với \(G\) là trọng tâm của \(\Delta ABC.\) Điền số thích hợp vào chỗ chấm: \(BE = ....GE\).

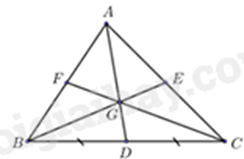
A. \(\frac{2}{3}\).

B. 2.

C. \(\frac{1}{2}\).

D. 3.

Phương pháp

Dựa vào tính chất trọng tâm của tam giác.

Lời giải

Vì G là trọng tâm của \(\Delta ABC\) nên \(GE = \frac{1}{3}BE\), suy ra \(BE = 3GE\).

Đáp án: D.

Phần tự luận.

Bài 1. (1,5 điểm)

a) Tính: \(\sqrt {\frac{{25}}{{16}}} .1,5 + {\left( {0,25} \right)^2}:\left| { - \frac{1}{4}} \right| - {\left( {\frac{{2023}}{{2024}}} \right)^0}\).

b) Tìm x, biết:

i. \(\frac{3}{4}x - \frac{1}{2} = 20\% \).

ii. \(\left| {x + \frac{3}{4}} \right| - \frac{2}{5} = 1\).

Phương pháp

a) Sử dụng kết hợp kiến thức về căn bậc hai, giá trị tuyệt đối, luỹ thừa và tính toán với số thực để tính.

b) i) Đưa về số hữu tỉ và sử dụng quy tắc chuyển vế để tìm x.

ii) Sử dụng quy tắc chuyển vế, đối với giá trị tuyệt đối ta chia hai trường hợp.

Lời giải

a) \(\sqrt {\frac{{25}}{{16}}} .1,5 + {\left( {0,25} \right)^2}:\left| { - \frac{1}{4}} \right| - {\left( {\frac{{2023}}{{2024}}} \right)^0}\)

\(\begin{array}{l} = \frac{5}{4}.\frac{3}{2} + {\left( {\frac{1}{4}} \right)^2}:\frac{1}{4} - 1\\ = \frac{{15}}{8} + \frac{1}{4} - 1\\ = \frac{{15}}{8} + \frac{2}{8} - \frac{8}{8}\\ = \frac{9}{8}\end{array}\)

b) i. \(\frac{3}{4}x - \frac{1}{2} = 20\% \).

\(\begin{array}{l}\frac{3}{4}x - \frac{1}{2} = \frac{1}{5}\\\frac{3}{4}x = \frac{1}{5} + \frac{1}{2}\\\frac{3}{4}x = \frac{7}{{10}}\\x = \frac{7}{{10}}:\frac{3}{4}\\x = \frac{{14}}{{15}}\end{array}\)

Vậy \(x = \frac{{14}}{{15}}\)

ii. \(\left| {x + \frac{3}{4}} \right| - \frac{2}{5} = 1\)

\(\begin{array}{l}\left| {x + \frac{3}{4}} \right| = 1 + \frac{2}{5}\\\left| {x + \frac{3}{4}} \right| = \frac{7}{5}\end{array}\)

\(x + \frac{3}{4} = \frac{7}{5}\) hoặc \(x + \frac{3}{4} =  - \frac{7}{5}\)

TH1: \(x + \frac{3}{4} = \frac{7}{5}\)

\(\begin{array}{l}x = \frac{7}{5} - \frac{3}{4}\\x = \frac{{13}}{{20}}\end{array}\)

TH2: \(x + \frac{3}{4} =  - \frac{7}{5}\)

\(\begin{array}{l}x =  - \frac{7}{5} - \frac{3}{4}\\x = \frac{{ - 43}}{{20}}\end{array}\)

Vậy \(x \in \left\{ {\frac{{13}}{{20}};\frac{{ - 43}}{{20}}} \right\}\)

Bài 2. (1,5 điểm)

a) Một nhà thầu ước tính rằng có thể hoàn thành một hợp đồng xây dựng trong 12 tháng với 280 công nhân. Nếu được yêu cầu phải hoàn hoàn thành hợp đồng trong 10 tháng thì nhà thầu đó phải thuê bao nhiêu công nhân (biết năng suất lao động của mỗi công nhân là như nhau)?

b) Chứng minh giá trị của đa thức \(f\left( x \right) = x\left( {1 - 2x} \right) + \left( {2{x^2} - x + 4} \right)\) không phụ thuộc vào \(x\).

Phương pháp

a) Gọi \(x\) (người) là số công nhân nhà thầu phải thuê (x > 0).

Do số người và thời gian là hai đại lượng tỉ lệ nghịch nên sử dụng tính chất của đại lượng tỉ lệ nghịch để tìm x.

b) Sử dụng quy tắc nhân đơn thức với đa thức, cộng đa thức để tính giá trị của đa thức.

Nếu sau khi rút gọn, đa thức không còn chứa x thì giá trị của đa thức không phụ thuộc vào x.

Lời giải

a) Gọi \(x\) (người) là số công nhân nhà thầu phải thuê (x > 0).

Do số người và thời gian là hai đại lượng tỉ lệ nghịch nên \(12.280 = 10.x\)

Suy ra \(x = \frac{{12.280}}{{10}} = 336\) (người)

Vậy cần 336 người để hoàn thành công trình trong 10 tháng.

b) Ta có: \(f\left( x \right) = x\left( {1 - 2x} \right) + \left( {2{x^2} - x + 4} \right)\)

\(\begin{array}{l} = x - 2{x^2} + 2{x^2} - x + 4\\ = \left( { - 2{x^2} + 2{x^2}} \right) + \left( {x - x} \right) + 4\\ = 0 + 0 = 4\end{array}\)

Vì \(f\left( x \right) = 4\) với mọi \(x\) nên giá trị của đa thức \(f\left( x \right)\) không phụ thuộc vào \(x\).

Bài 3. (1 điểm) Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên. Tính thể tích của thùng xe và diện tích phần Inox đóng thùng xe (tính luôn sàn).

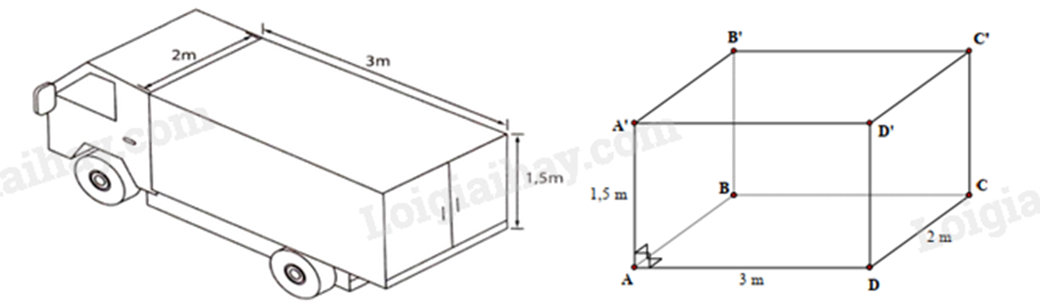
Phương pháp

- Sử dụng công thức tính thể tích hình hộp chữ nhật: V = chiều dài. chiều rộng. chiều cao.

- Diện tích phần Inox đóng thùng xe chính là diện tích toàn phần của hình hộp chữ nhật.

S_tp = S_xq + 2S_đáy.

S_xq = chu vi đáy. chiều cao.

Lời giải

Thể tích thùng xe là: \(3.2.1,5 = 9\left( {{m^3}} \right)\).

Diện tích xung quanh Inox đóng thùng xe là: \(2\left( {3 + 2} \right).1,5 = 15\left( {{m^2}} \right)\).

Diện tích toàn phần Inox đóng thùng xe là: \(15 + 2.3.2 = 27\left( {{m^2}} \right)\).

Vậy thể tích thùng xe là \(9{m^3}\), diện tích phần Inox đóng thùng xe là \(27{m^2}\).

Bài 4. (2,5 điểm) Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Vẽ AD vuông góc với BC (\(D \in BC\)).

a) Tính số đo các góc còn lại của tam giác ABC.

b) Chứng minh: \(\Delta ADB = \Delta ADC\).

c) Gọi M là trung điểm của DB. Từ M vẽ đường thẳng vuông góc với BC cắt AB tại E. Chứng minh:  DE // AC.

Phương pháp

a) Sử dụng tính chất của tam giác cân: hai góc ở đáy bằng nhau.

Định lí tổng ba góc trong tam giác bằng \(180^\circ \).

b) Chứng minh \(\Delta ADB = \Delta ADC\) (ch – cgv)

c) Chứng minh \(\Delta EMB = \Delta EMD\) (c–g-c) suy ra \(\widehat {EBM} = \widehat {EDM}\) (hai góc tương ứng)

Suy ra \(\widehat {ACD} = \widehat {EDM}\) và ở vị trí đồng vị nên ED // AC.

Lời giải

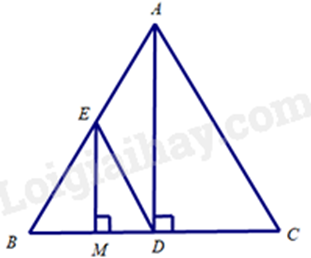
a) Vì tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \) nên \(\widehat {ACB} = \widehat {ABC} = 70^\circ \)

Theo định lí tổng ba góc trong tam giác, ta có:

\(\begin{array}{l}\widehat {BAC} = 180^\circ  - \left( {\widehat {ABC} + \widehat {ACB}} \right)\\ = 180^\circ  - \left( {70^\circ  + 70^\circ } \right)\\ = 40^\circ \end{array}\)

b) Xét \(\Delta ADB\) và \(\Delta ADC\) có:

\(\widehat {ADB} = \widehat {ADC}\left( { = 90^\circ } \right)\)

AD cạnh chung

AB = AC (\(\Delta ABC\) cân tại A)

nên \(\Delta ADB = \Delta ADC\) (ch – cgv)

c) Xét \(\Delta EMB\) và \(\Delta EMD\) có:

\(\widehat {EMB} = \widehat {EMD}\left( { = 90^\circ } \right)\)

EM cạnh chung

BM = DM (M là trung điểm BD)

nên \(\Delta EMB = \Delta EMD\) (c–g-c)

Suy ra \(\widehat {EBM} = \widehat {EDM}\) (hai góc tương ứng)

Mà \(\widehat {EBM} = \widehat {ACD}\) nên \(\widehat {ACD} = \widehat {EDM}\)

Mặt khác \(\widehat {EDM}\) và \(\widehat {ACD}\) ở vị trí đồng vị nên ED // AC.

Bài 5. (0,5 điểm) Có một chi tiết máy (đường viền ngoài là đường tròn) bị gãy (hình vẽ). Làm thế nào xác định được bán kính của đường viền này.

Phương pháp

Sử dụng kiến thức về sự đồng quy của các đường đặc biệt trong tam giác.

Lời giải

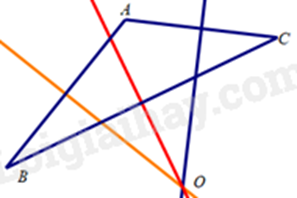
Gọi O là tâm của chi tiết máy.

Trên đường viền ta lấy ba điểm A, B, C không thẳng hảng.

Khi đó bán kính của chi tiết máy là OA = OB = OC.

Do đó O là giao điểm của ba đường trung trực trong tam giác ABC.