Đề ôn hè Toán 7 lên 8 - Đề 5

Đề bài

Bài 1. (2,5 điểm)

1. Thực hiện phép tính:

a) \(\frac{1}{2} + \frac{{ - 3}}{4}\)

b) \(\sqrt {16}  + \frac{1}{2} - {2^2}\)

c) \(\frac{4}{9}.0,4 - \frac{4}{9}.\frac{7}{5}\)  

2. Tìm x biết:

a) \(\frac{x}{6} = \frac{8}{3}\)

b) \(\frac{x}{3} = \frac{y}{6}\) và \(x + y = 90\) 

Bài 2. (1 điểm)

a) Cho đa thức \(P(x) = 3{x^4} + 2{x^2} - 3{x^4} - 3{x^2} + 2x - 5\).

Thu gọn và sắp xếp các hạng tử của \(P(x)\) theo lũy thừa giảm dần của biến.

b) Tính giá trị của biểu thức \(A = 3{x^2} - 2x + 1\) tại x = 2.

Bài 3. (2 điểm)

1. Cho bảng thống kê về số lượng bài tập toán bạn Lan đã làm trong một tuần như sau:

a) Trong tuần, ngày nào bạn Lan làm được nhiều bài tập toán nhất? Ngày nào bạn làm được ít bài tập toán nhất?

b) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên.

2. Một hộp đựng 6 quả bóng có kích thước giống nhau và được đánh số lần lượt là: 1, 2, 3, 4, 5, 6. Lấy ngẫu nhiên một quả bóng trong hộp.

a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên?

A: “Lấy được quả bóng ghi số chẵn”; 

B: “Lấy được quả bóng ghi số tròn chục”;

C: “Lấy được quả bóng ghi số không vượt quá 7”

b) Tính xác suất của biến cố A.

Bài 4. (1,5 điểm)

1. Hưởng ứng phong trào kế hoạch nhỏ của Đội, ba lớp 7A, 7B, 7C đã thu được tổng cộng 330kg giấy vụn. Biết rằng số giấy vụn thu được của ba lớp tỉ lệ với 4; 5; 6. Hãy tính số kg giấy vụn mỗi lớp thu được?

2. Một hình lập phương có cạnh 10cm. Tính diện tích xung quanh, thể tích của hình lập phương đó.

Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC). Kẻ BD là tia phân giác của \(\widehat {ABC}\) (D \( \in \) AC).Trên cạnh BC lấy điểm E sao cho AB = BE.

a) Chứng minh \(\Delta ABD = \Delta EBD\). Từ đó suy ra DA = DE.

b) So sánh DA và DC?

c) Đường thẳng ED cắt AB tại F. Gọi S là trung điểm của FC. Chứng minh ba: điểm B, D, S thẳng hàng.

Bài 6. (0,5 điểm) Tìm \(x,y,z\) biết: \(\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2}\) và \(x - 2y + 3z = 8\).

-------- Hết --------

Lời giải

Bài 1. (2,5 điểm)

1. Thực hiện phép tính:

a) \(\frac{1}{2} + \frac{{ - 3}}{4}\)

b) \(\sqrt {16}  + \frac{1}{2} - {2^2}\)

c) \(\frac{4}{9}.0,4 - \frac{4}{9}.\frac{7}{5}\)  

2. Tìm x biết:

a) \(\frac{x}{6} = \frac{8}{3}\)

b) \(\frac{x}{3} = \frac{y}{6}\) và \(x + y = 90\) 

Phương pháp

1. Thực hiện phép tính với số thực.

2.

a) Sử dụng tính chất của tỉ lệ thức: Từ \(\frac{a}{b} = \frac{c}{d}\) suy ra \(a = \frac{{b.c}}{d}\).

b) Sử dụng tính chất của dãy tỉ số bằng nhau: \(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}}\).

Lời giải

1.

a) \(\frac{1}{2} + \frac{{ - 3}}{4}{\rm{  =  }}\frac{2}{4} + \frac{{ - 3}}{4} = \frac{{2 + ( - 3)}}{4} = \frac{{ - 1}}{4}\)

b) \(\sqrt {16}  + \frac{1}{2} - {2^2} = 4 + \frac{1}{2} - 4 = (4 - 4) + \frac{1}{2} = \frac{1}{2}\)

c) \(\frac{4}{9}.0,4 - \frac{4}{9}.\frac{7}{5}\)\( = \frac{4}{9}.\frac{2}{5} - \frac{4}{9}.\frac{7}{5}\)\( = \frac{4}{9}.\left( {\frac{2}{5} - \frac{7}{5}} \right)\)\( = \frac{4}{9}.\left( { - 1} \right) =  - \frac{4}{9}\)

2.

a) \(\frac{x}{6} = \frac{8}{3}\)

\(\begin{array}{l}x = \frac{{8.6}}{3}\\x = 16\end{array}\)

Vậy \(x = 16\).

b) Áp dụng tính chất dãy tỉ số bằng nhau ta có

\(\frac{x}{3} = \frac{y}{6} = \frac{{x + y}}{{3 + 6}} = \frac{{90}}{9} = 10\)

Do đó: \(x = 10.3 = 30\)

\(y = 10.6 = 60\)

Vậy x = 30; y = 60

Bài 2. (1 điểm)

a) Cho đa thức \(P(x) = 3{x^4} + 2{x^2} - 3{x^4} - 3{x^2} + 2x - 5\).

Thu gọn và sắp xếp các hạng tử của \(P(x)\) theo lũy thừa giảm dần của biến.

b) Tính giá trị của biểu thức \(A = 3{x^2} - 2x + 1\) tại \(x = 2\).

Phương pháp

a) Thu gọn đa thức một biến: Thực hiện phép tính cộng (trừ) các đơn thức có cùng số mũ của biến.

Sắp xếp đa thức một biến: Viết đa thức dưới dạng thu gọn và sắp xếp các hạng tử của nó theo số mũ tăng dần (giảm dần) của biến.

b) Thay \(x = 2\) vào biểu thức A để tính.

Lời giải

a) \(P(x) = 3{x^4} + 2{x^2} - 3{x^4} - 3{x^2} + 2x - 5\)

\(\begin{array}{l}P(x) = (3{x^4} - 3{x^4}) + (2{x^2} - 3{x^2}) + 2x - 5\\P(x) =  - {x^2} + 2x - 5\end{array}\)

b) Thay \(x = 2\) vào biểu thức \(A = 3{x^2} - 2x + 1\) ta được:

\(A = {3.2^2} - 2.2 + 1\)

\(\begin{array}{l} = 3.4 - 4 + 1\\ = 12 - 4 + 1\\ = 9\end{array}\)

Vậy khi \(x = 2\) thì giá trị của biểu thức A bằng 9.

Bài 3. (2 điểm)

1. Cho bảng thống kê về số lượng bài tập toán bạn Lan đã làm trong một tuần như sau:

a) Trong tuần, ngày nào bạn Lan làm được nhiều bài tập toán nhất? Ngày nào bạn làm được ít bài tập toán nhất?

b) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên.

2. Một hộp đựng 6 quả bóng có kích thước giống nhau và được đánh số lần lượt là: 1, 2, 3, 4, 5, 6. Lấy ngẫu nhiên một quả bóng trong hộp.

a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên?

A: “Lấy được quả bóng ghi số chẵn”; 

B: “Lấy được quả bóng ghi số tròn chục”;

C: “Lấy được quả bóng ghi số không vượt quá 7”

b) Tính xác suất của biến cố A.

Phương pháp

1.

a) Quan sát bảng thống kê để trả lời.

b) Từ bảng thống kê, vẽ biểu đồ đoạn thẳng.

2.

a)

- Biến cố chắc chắn: là biến cố biết trước được luôn xảy ra.

- Biến cố không thể: là biến cố biết trước được không bao giờ xảy ra.

- Biến cố ngẫu nhiên: là biến cố không thể biết trước được có xảy ra hay không.

b) Biến cố ngẫu nhiên: Có k biến cố đồng khả năng và luôn xảy ra 1 trong k biến cố này thì xác suất của mỗi biến cố đó là \(\frac{1}{k}\).

Lời giải

1.

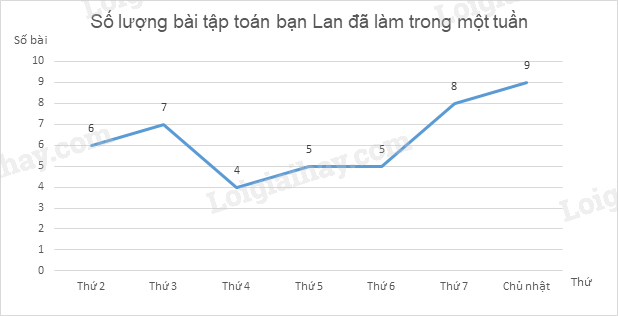
a) Bạn Lan làm được nhiều bài tập toán nhất vào Chủ nhật (9 bài).

Bạn Lan làm được ít bài tập toán nhất vào thứ 4 (4 bài).

b) Ta có biểu đồ đoạn thẳng:

2.

a) Biến cố A là biến cố ngẫu nhiên.

Biến cố B là biến cố không thể.

Biến cố C là biến cố chắc chắn.

b) Xét biến cố A “Lấy được quả bóng ghi số chẵn”: Có 3 khả năng xảy ra biến cố này: 2; 4; 6.

Xét biến cố “Lấy được quả bóng ghi số lẻ”: Có 3 khả năng xảy ra biến cố này: 1; 3; 5.

Khi đó hai biến cố là hai biến cố đồng khả năng và luôn xảy ra 1 trong 2 biến cố này.

Vậy xác suất của biến cố A là: \(\frac{1}{2}\).

Bài 4. (1,5 điểm)

1. Hưởng ứng phong trào kế hoạch nhỏ của Đội, ba lớp 7A, 7B, 7C đã thu được tổng cộng 330kg giấy vụn. Biết rằng số giấy vụn thu được của ba lớp tỉ lệ với 4; 5; 6. Hãy tính số kg giấy vụn mỗi lớp thu được?

2. Một hình lập phương có cạnh 10cm. Tính diện tích xung quanh, thể tích của hình lập phương đó.

Phương pháp

1. Gọi khối lượng giấy vụn thu được của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\) (kg)

Theo bài ra ta có \(\frac{x}{4} = \frac{y}{5} = \frac{z}{6}\;\) và \(x + y + z = 330\)

Áp dụng tính chất dãy tỉ số bằng nhau để tìm \(x,y,z\).

2. Diện tích xung quanh của hình lập phương: \({S_{xq}} = 4.{a^2}\)

Thể tích của hình lập phương là: \(V = {a^3}\)

(a là độ dài cạnh)

Lời giải

1. Gọi khối lượng giấy vụn thu được của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\) (kg)

Theo bài ra ta có

\(\frac{x}{4} = \frac{y}{5} = \frac{z}{6}\;\) và \(x + y + z = 330\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có

\(\frac{x}{4} = \frac{y}{5} = \frac{z}{6} = \frac{{x + y + z}}{{4 + 5 + 6}} = \frac{{330}}{{15}} = 22\)

Do đó: \(x = 22.4 = 88;\;\;y = 22.5 = 110;\;\;z = 22.6 = 132\)

Vậy khối lượng giấy vụn thu được của ba lớp 7A, 7B, 7C lần lượt là 88kg; 110kg và 132kg.

2. Diện tích xung quanh của hình lập phương là:

\({S_{xq}} = {4.10^2} = 4.100 = 400\left( {c{m^2}} \right)\)

Thể tích của hình lập phương là:

\(V = {10^3} = 1000\left( {c{m^3}} \right)\)

Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC). Kẻ BD là tia phân giác của \(\widehat {ABC}\) (D \( \in \) AC).Trên cạnh BC lấy điểm E sao cho AB = BE.

a) Chứng minh \(\Delta ABD = \Delta EBD\). Từ đó suy ra DA = DE.

b) So sánh DA và DC?

c) Đường thẳng ED cắt AB tại F. Gọi S là trung điểm của FC. Chứng minh ba: điểm B, D, S thẳng hàng.

Phương pháp

a) Chứng minh \(\Delta ABD\) = \(\Delta EBD\) (c.g.c)

suy ra AD = ED (2 cạnh tương ứng)

b) Chứng minh BC \( \bot \) DE nên \(\Delta DEC\) vuông tại E

Suy ra cạnh huyền DC > DE nên DC > DA

c) Chứng minh B nằm trên đường trung trực của CF (1)

Chứng minh D nằm trên đường trung trực của CF (2)

Chứng minh S nằm trên đường trung trực của CF (3)

Từ (1), (2), (3) suy ra ba điểm B, D, S thẳng hàng.

Lời giải

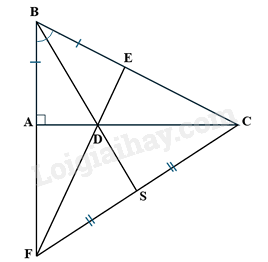
a) Xét DABD và DEBD  có  

BD là cạnh chung     

\(\widehat {ABD} = \widehat {EBD}\) (vì BD là tia phân giác của \(\widehat {ABC}\))

AB = EB (gt)

nên \(\Delta ABD\) = \(\Delta EBD\) (c.g.c)

suy ra AD = ED (2 cạnh tương ứng)

b) Do \(\Delta ABD\) = \(\Delta EBD\) nên \(\widehat {BAD} = \widehat {BED} = 90^\circ \)

Suy ra BE \( \bot \) DE hay BC \( \bot \) DE

Do đó \(\Delta DEC\) vuông tại E

Xét \(\Delta DEC\) vuông tại E ta có: DC > DE (cạnh huyền là cạnh lớn nhất)

Mà DE = DA (theo chứng minh phần a)

suy ra DC > DA

c) Xét \(\Delta DAF\) và \(\Delta DEC\) có:

\(\widehat {DAF} = \widehat {DEC}\left( { = 90^\circ } \right)\)

AD = ED

\(\widehat {ADF} = \widehat {EDC}\) (hai góc đối đỉnh)

nên \(\Delta DAF = \Delta DEC\) (g.c.g)

suy ra AF = EC (hai cạnh tương ứng)

Do đó: AB + AF = EB + EC hay BF = BC

Suy ra B nằm trên đường trung trực của CF (1)

Do \(\Delta DAF = \Delta DEC\) (cmt) nên DF = DC (hai cạnh tương ứng)

Suy ra D nằm trên đường trung trực của CF (2)

Mặt khác: S là trung điểm của CF  nên S nằm trên đường trung trực của CF (3)

Từ (1), (2), (3) suy ra ba điểm B, D, S thẳng hàng.

Bài 6. (0,5 điểm) Tìm \(x,y,z\) biết: \(\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2}\) và \(x - 2y + 3z = 8\).

Phương pháp

Áp dụng tính chất của dãy tỉ số bằng nhau để chứng minh \(\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2} = 0\)

Suy ra dãy tỉ số bằng nhau mới.

Áp dụng tính chất của dãy tỉ số bằng nhau với \(x - 2y + 3z = 8\) để tìm \(x,y,z\).

Lời giải

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2}\\ = \frac{{4.\left( {3x - 2y} \right)}}{{4.4}} = \frac{{3\left( {2z - 4x} \right)}}{{3.3}} = \frac{{2\left( {4y - 3z} \right)}}{{2.2}}\\ = \frac{{12x - 8y + 6z - 12x + 8y - 6z}}{{16 + 9 + 4}}\\ = \frac{0}{{29}} = 0\end{array}\)

Suy ra:

+) \(\frac{{3x - 2y}}{4} = 0\)

\(\begin{array}{l}3x - 2y = 0\\\frac{x}{2} = \frac{y}{3}\,\,\,\left( 1 \right)\end{array}\)

+) \(\frac{{2z - 4x}}{3} = 0\)

\(\begin{array}{l}2z - 4x = 0\\\frac{x}{2} = \frac{z}{4}\,\,\,\left( 2 \right)\end{array}\)

Từ (1) và (2) suy ra: \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{12}} = \frac{{x - 2y + 3z}}{{2 - 6 + 12}} = \frac{8}{8} = 1\)

Suy ra \(\frac{x}{2} = 1\) nên \(x = 2\);

           \(\frac{y}{3} = 1\) nên \(y = 3\);

           \(\frac{z}{4} = 1\) nên \(z = 4\).

Vậy \(x = 2;y = 3;z = 4\).