Dạng bài tam giác cân, vuông, vuông cân, đều - Ôn hè Toán 7 lên 8

Lý thuyết

* Tam giác cân:

- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

+ Hai cạnh bằng nhau được gọi là hai cạnh bên.

+ Cạnh còn lại là cạnh đáy.

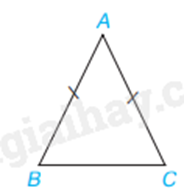
\(\Delta ABC\) cân tại A khi và chỉ khi AB = AC.

- Tính chất: Trong tam giác cân, hai góc ở đáy bằng nhau.

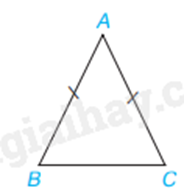
\(\Delta ABC\) cân tại A suy ra \(\widehat B = \widehat C\).

- Dấu hiệu nhận biết:

+ Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

+ Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

* Tam giác vuông:

- Định nghĩa: Tam giác vuông là tam giác có một góc vuông.

+ Hai cạnh kề góc vuông là hai cạnh góc vuông

+ Cạnh còn lại là cạnh huyền.

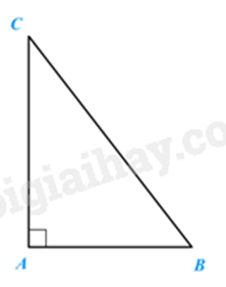
\(\Delta ABC\) vuông tại A khi và chỉ khi \(\widehat A = 90^\circ \).

AB, AC là hai cạnh góc vuông, BC là cạnh huyền.

- Tính chất: Trong tam giác vuông, hai góc nhọn phụ nhau.

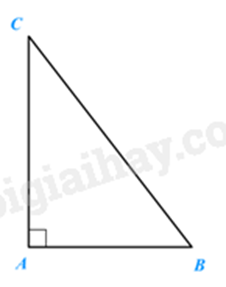
\(\Delta ABC\) vuông tại A suy ra \(\widehat B + \widehat C = 90^\circ \).

- Dấu hiệu nhận biết:

+ Nếu một tam giác có một góc vuông thì tam giác đó là tam giác vuông.

+ Nếu một tam giác có hai góc phụ nhau thì tam giác đó là tam giác vuông.

* Tam giác vuông cân

- Định nghĩa: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

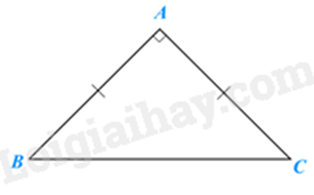
\(\Delta ABC\) vuông cân tại A khi và chỉ khi \(\widehat A = 90^\circ \) và AB = AC.

- Tính chất: Mỗi góc nhọn của tam giác vuông cân bằng \(45^\circ \).

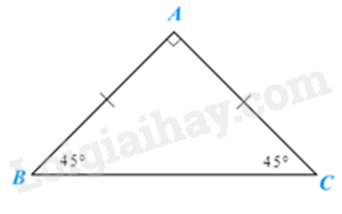
\(\Delta ABC\) vuông cân tại A thì \(\widehat B = \widehat C = 45^\circ \).

- Dấu hiệu nhận biết:

+ Tam giác vuông có hai cạnh góc vuông bằng nhau là tam giác vuông cân.

+ Tam giác vuông có một góc nhọn bằng \(45^\circ \) là tam giác vuông cân.

+ Tam giác cân có một góc vuông là tam giác vuông cân.

* Tam giác đều

- Định nghĩa:

Tam giác đều là tam giác có ba cạnh bằng nhau.

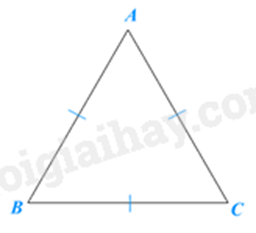
\(\Delta ABC\) đều khi và chỉ khi AB = BC = CA.

- Tính chất: Tam giác đều có mỗi góc bằng \(60^\circ \).

- Dấu hiệu nhận biết:

+ Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.

+ Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

+ Nếu tam giác cân có một góc bằng \(60^\circ \) thì tam giác đó là tam giác đều.

Bài tập

Bài 1: Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:

A. \(\hat B = \hat C\).

B. \(\hat C = \frac{{180^\circ  - \hat A}}{2}\).

C. \(\hat A = 180^\circ  - 2\hat C\).

D. \(\hat B \ne \hat C\).

Bài 2: Một tam giác cân có góc ở đỉnh bằng \(54^\circ \) thì số đo góc ở đáy là:

A. \(54^\circ \).

B. \(63^\circ \).

C. \(72^\circ \).

D. \(90^\circ \).

Bài 3: Phát biểu nào sau đây là đúng:

A. Góc ở đỉnh của một tam giác cân thì nhỏ hơn \(90^\circ \).

B. Trong một tam giác bất kì góc lớn nhất là góc tù.

C. Trong một tam giác vuông có thể có một góc tù.

D. Góc ở đáy của một tam giác cân không thể là góc tù.

Bài 4: Cho tam giác ABC cân tại đỉnh A với \(\hat A = 80^\circ \). Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho AD = AE. Phát biểu nào sau đây là sai?

A. DE // BC.

B. \(\hat B = 50^\circ \).

C. \(\widehat {ADE} = 50^\circ \).

D. Cả ba phát biểu trên đều sai.

Bài 5: Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).

A. 30\(^\circ \).

B. 45\(^\circ \).

C. 67,5\(^\circ \).

D. 60\(^\circ \).

Bài 6: Trong các tam giác trên các hình Ha, Hb, Hc, Hd sau đây đâu là tam giác cân, vuông cân, đều? Vì sao?

a)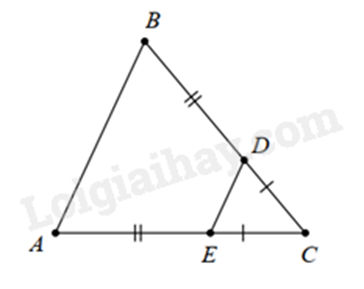 

b)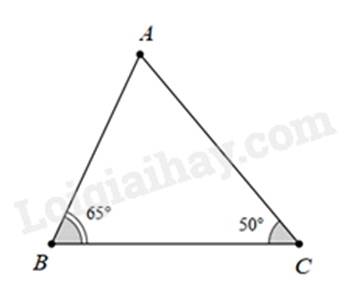 

c)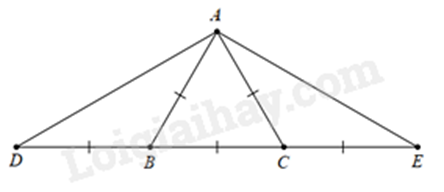 

d)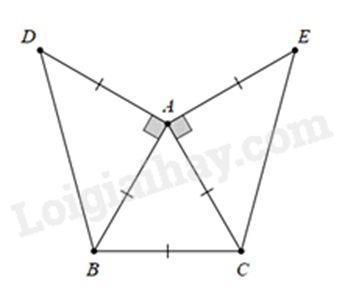 

Bài 7:

a) Vẽ tam giác \(ABC\) cân tại \(A\) có cạnh bên bằng \(3{\rm{cm}}\), cạnh đáy bằng \(4{\rm{cm}}\).

b) Vẽ tam giác vuông cân có cạnh bên là \(3{\rm{cm}}\).

c) Vẽ tam giác đều \(ABC\) có cạnh bằng \(4{\rm{cm}}\).

(Dùng thước có chia centimet và compa, tất cả các trường hợp đều nêu từng bước vẽ).

Bài 8: Cho tam giác ABC cân tại A có \(\hat B = \hat C = {50^ \circ }\). Trên tia đối của tia BC lấy điểm D sao cho BD = BA, trên tia đối của tia CB lấy E sao cho CE = CA. Tính số đo góc DAE?

Bài 9: Cho tam giác ABC vuông cân tại A, trên tia đối của tia BA lấy D sao cho BD = BC

a) Tính số đo các góc của \(\Delta ADC\)?

b) Trên tia đối của tia BC lấy điểm E sao cho BE = BC. Tính số đo các góc của \(\Delta CDE\)?

Bài 10: Cho \(\Delta ABC\) cân tại \(A\), các điểm \(E,F\) lần lượt nằm trên các cạnh \(AC,AB\) sao cho \(BE\) vuông góc với \(AC,CF\) vuông góc với \(AB\)

a) Chứng minh rằng \(BE = CF\)

b) Gọi \(I\) là giao điểm của \(BE\) và \(CF\), chứng minh \(\Delta BIC\) cân tại \(I\).

Bài 11: Cho \(\Delta ABC\) cân tại \(A\). Gọi \(M\) là trung điểm của \(BC\). Chứng minh \(AM\) vuông góc với \(BC\) và \(AM\) là tia phân giác của góc \(\widehat {BAC}\).

Bài 12: Cho \(\Delta ABC\) cân tại \(A\). Lấy điểm \(D\) thuộc cạnh \(AC\), \(E\) thuộc cạnh \(AB\) sao cho \(AD = AE\).

a) Chứng minh \(BD = CE\)

b) Gọi \(I\) là giao điểm của \(BD\) và \(CE\). Chứng minh \(\Delta IBC\) và \(\Delta IED\) là các tam giác cân.

c) Chứng minh \(DE\parallel BC\).

--------Hết--------

Lời giải chi tiết:

Bài 1: Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:

A. \(\hat B = \hat C\).

B. \(\hat C = \frac{{180^\circ  - \hat A}}{2}\).

C. \(\hat A = 180^\circ  - 2\hat C\).

D. \(\hat B \ne \hat C\).

Phương pháp

Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.

Lời giải

Do tam giác ABC cân nên \(\hat B = \hat C\)

Xét tam giác ABC ta có:

\(\hat A + \hat B + \hat C = 180^\circ \)

\(\hat B + \hat C = 180^\circ  - \hat A\)

\(\hat C = \frac{{180^\circ  - \hat A}}{2}\)

hay \(\hat A = 180^\circ  - 2\hat C\)

Đáp án: D

Bài 2: Một tam giác cân có góc ở đỉnh bằng \(54^\circ \) thì số đo góc ở đáy là:

A. \(54^\circ \).

B. \(63^\circ \).

C. \(72^\circ \).

D. \(90^\circ \).

Phương pháp

Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.

Lời giải

Do tam giác ABC cân nên \(\hat B = \hat C\)

Xét tam giác ABC ta có:

\(\begin{array}{l}\hat A + \hat B + \hat C = 180^\circ \\\hat B + \hat C = 180^\circ  - \hat A\\\hat C = \frac{{180^\circ  - \hat A}}{2} = \frac{{180^\circ  - 54^\circ }}{2} = 63^\circ \end{array}\)

Đáp án: B

Bài 3: Phát biểu nào sau đây là đúng:

A. Góc ở đỉnh của một tam giác cân thì nhỏ hơn \(90^\circ \).

B. Trong một tam giác bất kì góc lớn nhất là góc tù.

C. Trong một tam giác vuông có thể có một góc tù.

D. Góc ở đáy của một tam giác cân không thể là góc tù.

Phương pháp

Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.

Lời giải

Giả sử xét trong tam giác ABC cân tại A.

Xét tam giác ABC ta có:

\(\hat A + \hat B + \hat C = 180^\circ \)

\(\hat B + \hat C = 180^\circ  - \hat A\)

\(\hat C = \frac{{180^\circ  - \hat A}}{2}\)

Vì \(180^\circ  - \hat A < 180^\circ {\rm{\;}}\) nên \(\frac{{180^\circ  - \hat A}}{2} < \frac{{180^\circ }}{2} = 90^\circ \)

Vậy góc ở đáy của một tam giác cân không thể là góc tù.

Đáp án: D

Bài 4: Cho tam giác ABC cân tại đỉnh A với \(\hat A = 80^\circ \). Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho AD = AE. Phát biểu nào sau đây là sai?

A. DE // BC.

B. \(\hat B = 50^\circ \).

C. \(\widehat {ADE} = 50^\circ \).

D. Cả ba phát biểu trên đều sai.

Phương pháp

Sử dụng tính chất tam giác cân, tính chất tổng các góc của một tam giác, dấu hiệu nhận biết hai đường thẳng song song.

Lời giải

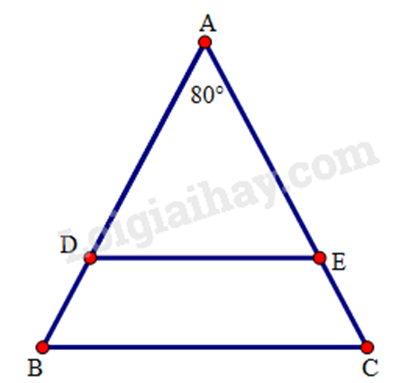
Do tam giác ABC cân tại A nên \(\hat B = \frac{{180^\circ  - \hat A}}{2} = \frac{{180^\circ  - 80^\circ }}{2} = 50^\circ \)

Ta thấy tam giác ADE cân do AD = AE

suy ra \(\widehat {ADE} = \frac{{180^\circ  - \hat A}}{2} = \frac{{180^\circ  - 80^\circ }}{2} = 50^\circ \)

Do đó \(\hat B = \widehat {ADE}\) .

Mà hai góc này ở vị trí đồng vị nên ED // BC (Dấu hiệu nhận biết 2 đường thẳng song song)

Vậy D là đáp án sai.

Đáp án: D

Bài 5: Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).

A. 30\(^\circ \).

B. 45\(^\circ \).

C. 67,5\(^\circ \).

D. 60\(^\circ \).

Phương pháp

Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân, tính được \(\widehat {ANM},\widehat {AMN}\) suy ra số đo góc MAN.

Lời giải

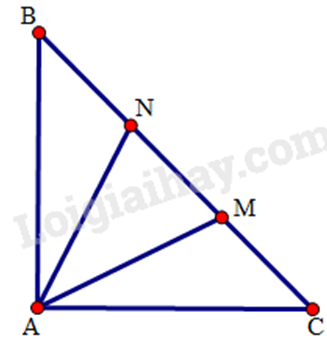
Do tam giác ABC vuông cân ở A nên \(\hat B = \hat C = 45^\circ \).

Xét tam giác AMB có: BM = BA (gt), nên tam giác AMB cân ở B.

Do đó \(\widehat {AMB} = \frac{{180^\circ  - \hat B}}{2} = \frac{{180^\circ  - 45^\circ }}{2} = 67,5^\circ \)

Chứng minh tương tự ta được tam giác ANC cân ở C và \(\widehat {ANC} = 67,5^\circ \).

Xét tam giác AMN, ta có:

\(\widehat {MAN} = 180^\circ  - \left( {\widehat {AMN} + \widehat {ANM}} \right) = 180^\circ  - \left( {67,5^\circ  + 67,5^\circ } \right) = 45^\circ \).

Vậy \(\widehat {MAN} = 45^\circ \)

Đáp án: B

Bài 6: Trong các tam giác trên các hình Ha, Hb, Hc, Hd sau đây đâu là tam giác cân, vuông cân, đều? Vì sao?

a)

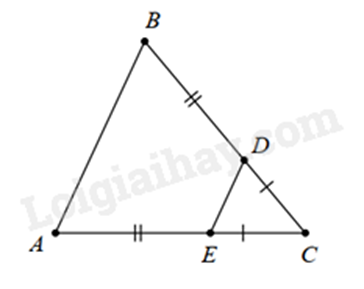
b)

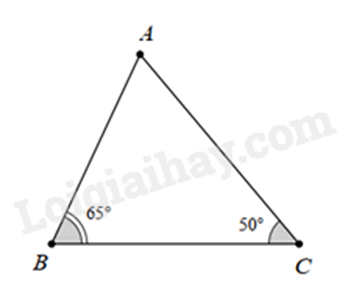
c)

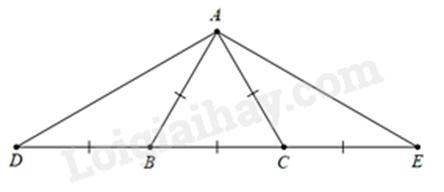
d)

Phương pháp

- Dấu hiệu nhận biết tam giác cân:

+ Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

+ Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

- Dấu hiệu nhận biết tam giác vuông:

+ Nếu một tam giác có một góc vuông thì tam giác đó là tam giác vuông.

+ Nếu một tam giác có hai góc phụ nhau thì tam giác đó là tam giác vuông.

- Dấu hiệu nhận biết tam giác vuông cân:

+ Tam giác vuông có hai cạnh góc vuông bằng nhau là tam giác vuông cân.

+ Tam giác vuông có một góc nhọn bằng \(45^\circ \) là tam giác vuông cân.

+ Tam giác cân có một góc vuông là tam giác vuông cân.

- Dấu hiệu nhận biết tam giác đều:

+ Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.

+ Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

+ Nếu tam giác cân có một góc bằng \(60^\circ \) thì tam giác đó là tam giác đều.

Lời giải

a)

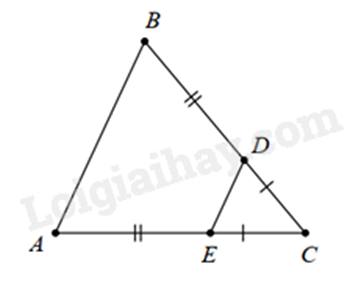
Vì \(CD = CE\) nên \(\Delta CDE\) cân tại C.

Mà \(DB = AE\)

nên \(CD + DB = CE + EA\)

suy ra \(CB = CA\). Do đó \(\Delta CBA\) cân tại C.

b)

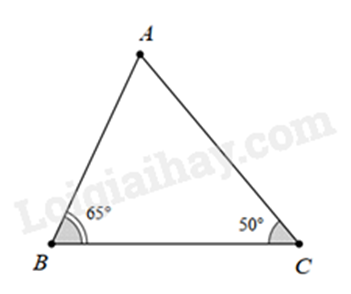
Ta có: \(\hat A + \hat B + \hat C = {180^ \circ }\)

Suy ra \(\hat A = {180^ \circ } - \left( {\hat B + \hat C} \right) = {180^ \circ } - \left( {{{65}^ \circ } + {{50}^ \circ }} \right) = {65^ \circ }\)

Xét \(\Delta ABC\) có: \(\hat A = \hat B = {65^ \circ }\) nên \(\Delta ABC\) cân tại C

c)

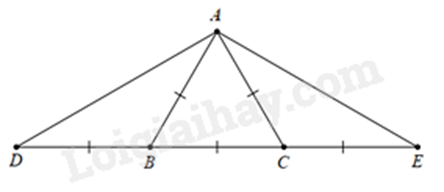
Ta có: \(AB = BC = CA\) nên \(\Delta ABC\) đều.

Lại có: \(DB = AB\) nên \(\Delta ABD\) cân tại B.

Tương tự, ta có \(\Delta ACE\) cân tại C.

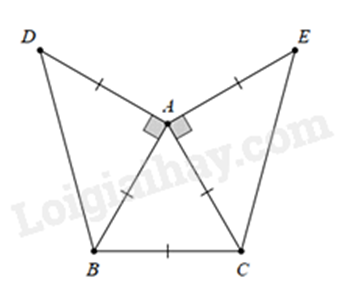
d)

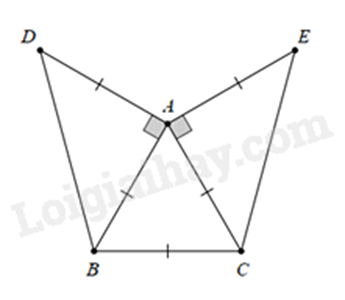
Ta có: \(AB = BC = CA\) nên \(\Delta ABC\) đều.

Ta có: \(\widehat {BAD} = {90^ \circ }\) và \(AB = AD\) nên \(\Delta ABD\) vuông cân tại \(A\).

Chứng minh tương tự ta có \(\Delta ACE\) vuông cân tại \(A\).

Bài 7:

a) Vẽ tam giác \(ABC\) cân tại \(A\) có cạnh bên bằng \(3{\rm{cm}}\), cạnh đáy bằng \(4{\rm{cm}}\).

b) Vẽ tam giác vuông cân có cạnh bên là \(3{\rm{cm}}\).

c) Vẽ tam giác đều \(ABC\) có cạnh bằng \(4{\rm{cm}}\).

(Dùng thước có chia centimet và compa, tất cả các trường hợp đều nêu từng bước vẽ).

Phương pháp

Dựa vào các đặc điểm của tam giác cân, tam giác vuông cân, tam giác đều để vẽ.

Lời giải

a) Vẽ đoạn thẳng \(BC = 4{\rm{cm}}\).

Lấy \(B\) làm tâm vẽ đường tròn tâm \(B\) bán kính \(3{\rm{cm}}\).

Tương tự lấy \(C\) làm tâm vẽ đường tròn tâm \(C\) bán kính \(3{\rm{cm}}\).

Lấy \(A\) là giao điểm của hai đường tròn \(\left( {B;3{\rm{cm}}} \right)\) và \(\left( {C;3{\rm{cm}}} \right)\). Nối \(A\) với \(B\), \(A\) với \(C\) ta được \(\Delta ABC\) cân cần vẽ.

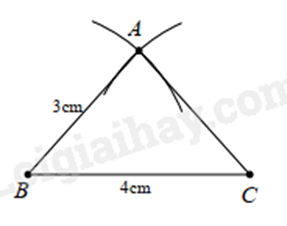
b) Vẽ \(\widehat {xAy} = {90^ \circ }\).

Trên \(Ax\) lấy điểm \(B\) sao cho \(AB = 3{\rm{cm}}\).

Trên \(Ay\) lấy điểm \(C\) sao cho \(AC = 3{\rm{cm}}\).

Nối \(B\) và \(C\) ta được \(\Delta ABC\) vuông cân tại \(A\).

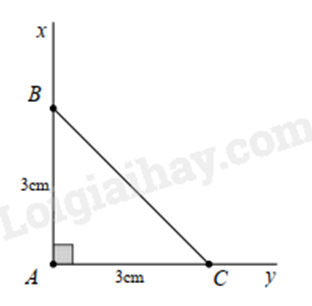
c) Vẽ đoạn thẳng \(BC = 4{\rm{cm}}\).

Lấy \(B\) làm tâm vẽ đường tròn tâm \(B\) bán kính \(4{\rm{cm}}\).

Tương tự lấy \(C\) làm tâm vẽ đường tròn tâm \(C\) bán kính \(4{\rm{cm}}\).

Lấy \(A\) là giao điểm của hai đường tròn \(\left( {B;4{\rm{cm}}} \right)\) và \(\left( {C;4{\rm{cm}}} \right)\). Nối \(A\) với \(B\), \(A\) với \(C\) ta được \(\Delta ABC\) cần vẽ.

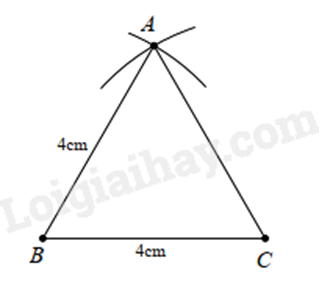
Bài 8: Cho tam giác ABC cân tại A có \(\hat B = \hat C = {50^ \circ }\). Trên tia đối của tia BC lấy điểm D sao cho BD = BA, trên tia đối của tia CB lấy E sao cho CE = CA. Tính số đo góc DAE?

Phương pháp

Sử dụng kiến thức về hai góc kề bù để tính \(\widehat {ABD}\), \(\widehat {ACE}\).

Chứng minh tam giác ABD, tam giác ACE cân tại B và C nên áp dụng tổng ba góc trong tam giác bằng \(180^\circ \) tính được \(\widehat {BAD},\widehat {CAE}\).

Tam giác ABC cân tại A nên ta tính được \(\widehat {BAC}\).

Tính góc DAE = \(\widehat {BAD} + \widehat {BAC} + \widehat {CAE}\).

Lời giải

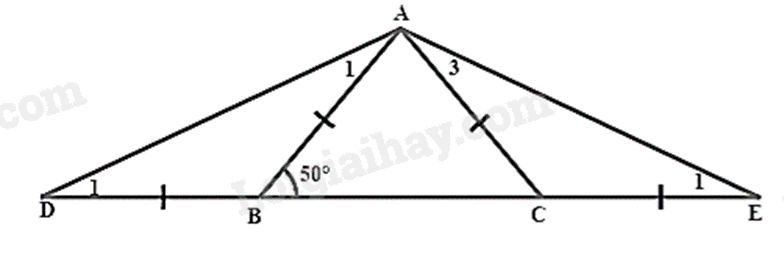
Ta có: \(\hat B + \widehat {ABD} = {180^ \circ }\) (kề bù)

\({50^ \circ } + \widehat {ABD} = {180^ \circ }\)

suy ra \(\widehat {ABD} = {180^ \circ } - {50^ \circ } = {130^ \circ }\)

Vì \(\Delta ABD\) cân tại B (BD = BA (gt)) nên \(\widehat {{D_1}} = \widehat {{A_1}} = \frac{{{{180}^ \circ } - \widehat {ABD}}}{2} = \frac{{{{180}^ \circ } - {{130}^ \circ }}}{2} = {25^ \circ }\)

Tương tự với \(\Delta ACE\) cân tại C ta cũng có \(\widehat {{A_3}} = \widehat {{E_1}} = {25^ \circ }\)

Mặt khác: Xét \(\Delta ABC\) cân tại A có \(\hat B = {50^ \circ }\) nên \(\hat C = {50^ \circ }\)

Do đó \(\hat A = {180^ \circ } - 2\hat B = {180^ \circ } - {2.50^ \circ } = {80^ \circ }\)

Vậy \(\widehat {DAE} = \widehat {{A_1}} + \widehat {BAC} + \widehat {{A_3}} = {25^ \circ } + {80^ \circ } + {25^ \circ } = {130^ \circ }\)

Bài 9: Cho tam giác ABC vuông cân tại A, trên tia đối của tia BA lấy D sao cho BD = BC

a) Tính số đo các góc của \(\Delta ADC\)?

b) Trên tia đối của tia BC lấy điểm E sao cho BE = BC. Tính số đo các góc của \(\Delta CDE\)?

Phương pháp

a) \(\Delta ABC\) vuông cân tại A nên hai góc ở đáy bằng \(45^\circ \)

Kết hợp tính chất hai góc kề bù để tính \(\widehat {CBD}\).

\(\Delta BDC\) cân tại B nên tính được \(\widehat {BDC} = \widehat {BCD}\).

Tính \(\widehat {ACD} = \widehat {ACB} + \widehat {BCD}\).

b) \(\Delta BED\) cân tại B có \(\widehat {{B_2}} = \widehat {{B_1}} = {45^ \circ }\) nên tính được \(\hat E = \widehat {{D_2}}\).

suy ra tính được \(\widehat {EDC} = \widehat {EDB} + \widehat {BDC}\).

Lời giải

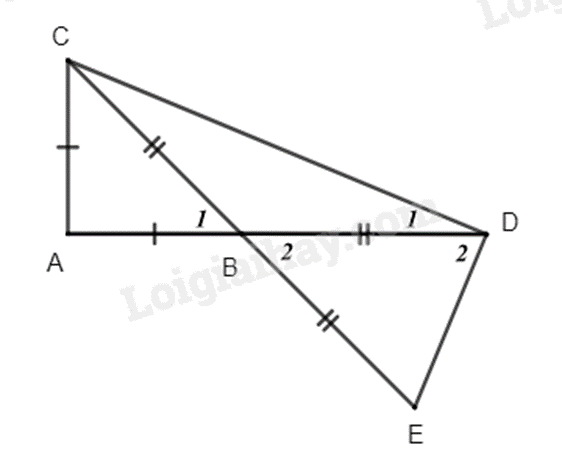
a) \(\Delta ABC\) vuông cân tại A nên \(\widehat {ABC} = \widehat {ACB} = {45^ \circ }\)

Mà: \(\widehat {ABC} + \widehat {CBD} = {180^ \circ }\) (kề bù)

\({45^ \circ } + \widehat {CBD} = {180^ \circ }\)

nên \(\widehat {CBD} = {180^ \circ } - {45^ \circ } = {135^ \circ }\)

Ta có \(\Delta BDC\) cân tại B (do BD = BC (gt)) nên \(\widehat {BDC} = \widehat {BCD} = \frac{{{{180}^ \circ } - \widehat {CBD}}}{2} = \frac{{{{180}^ \circ } - {{135}^ \circ }}}{2} = \frac{{{{45}^ \circ }}}{2}\)

Tia CB nằm giữa hai tia CA và CD, ta có:

\(\widehat {ACD} = \widehat {ACB} + \widehat {BCD} = {45^ \circ } + \frac{{{{45}^ \circ }}}{2} = \frac{{{{90}^ \circ } + {{45}^ \circ }}}{2} = \frac{{{{135}^ \circ }}}{2}\)

Vậy \(\widehat {CAD} = 90^\circ ,\widehat {ACD} = \frac{{135^\circ }}{2},\widehat {ADC} = \frac{{45^\circ }}{2}\).

b) \(\Delta BED\) cân tại B (BE = BD = BC) có \(\widehat {{B_2}} = \widehat {{B_1}} = {45^ \circ }\) nên \(\hat E = \widehat {{D_2}} = \frac{{{{180}^ \circ } - {{45}^ \circ }}}{2} = \frac{{{{135}^ \circ }}}{2}\)

suy ra \(\widehat {EDC} = \frac{{{{135}^ \circ }}}{2} + \frac{{{{45}^ \circ }}}{2} = \frac{{{{180}^ \circ }}}{2} = {90^ \circ }\).

Vậy \(\widehat {CDE} = 90^\circ ,\widehat {CED} = \frac{{135^\circ }}{2},\widehat {ECD} = \frac{{45^\circ }}{2}\).

Bài 10: Cho \(\Delta ABC\) cân tại \(A\), các điểm \(E,F\) lần lượt nằm trên các cạnh \(AC,AB\) sao cho \(BE\) vuông góc với \(AC,CF\) vuông góc với \(AB\)

a) Chứng minh rằng \(BE = CF\)

b) Gọi \(I\) là giao điểm của \(BE\) và \(CF\), chứng minh \(\Delta BIC\) cân tại \(I\).

Phương pháp

a) Chứng minh \(\Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn)

Suy ra \(BE = CF\) (hai cạnh tương ứng)

b) Để chứng minh \(\Delta BIC\) cân tại \(I\), ta có thể chứng minh theo 2 cách sau:

+ Cách 1: Hai cạnh bằng nhau

Chứng minh \(BF = CE\)

Do đó \(\Delta BFI = \Delta CEI\) (cạnh góc vuông – góc nhọn)

suy ra \(IB = IC\) (2 cạnh tương ứng) hay \(\Delta BIC\) cân tại \(I\).

+ Cách 2: Hai góc bằng nhau

Chứng minh \(\widehat {EBC} = \widehat {FCB}\) do đó \(\Delta BIC\) cân tại \(I\).

Lời giải

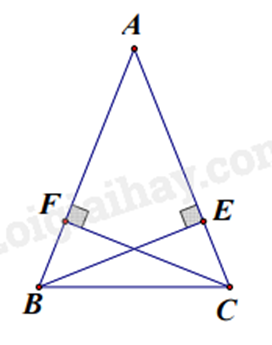
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:

\(\widehat {AEB} = \widehat {AFC} = {90^ \circ }\left( {gt} \right)\)

\(\widehat {BAC}\) góc chung

\(AB = AC\left( {gt} \right)\)

Do đó: \(\Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn)

Suy ra \(BE = CF\) (hai cạnh tương ứng)

b)

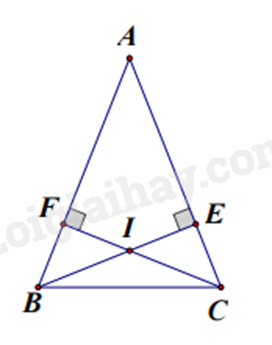
Cách 1: Ta có \(AB = AC\left( {gt} \right);AF = AE\left( {cmt} \right)\)

suy ra \(AB - AF = AC - AE\)

hay \(BF = CE\)

Xét \(\Delta BFI\) và \(\Delta CEI\) có:

\(\widehat {BFI} = \widehat {CEI} = {90^ \circ }\left( {gt} \right)\)

\(BF = CE\left( {cmt} \right)\)

\(\widehat {FBI} = \widehat {ECI}\left( {cmt} \right)\)

Do đó \(\Delta BFI = \Delta CEI\) (cạnh góc vuông – góc nhọn)

suy ra \(IB = IC\) (2 cạnh tương ứng) hay \(\Delta BIC\) cân tại \(I\).

Cách 2: Ta có \(\widehat {ABC} = \widehat {ABE} + \widehat {EBC}\); \(\widehat {ACB} = \widehat {ACF} + \widehat {FCB}\)

mà \(\widehat {ABC} = \widehat {ACB}\left( {gt} \right),\widehat {ABE} = \widehat {ACF}\left( {cmt} \right)\)

Do đó \(\widehat {EBC} = \widehat {FCB}\) hay \(\widehat {IBC} = \widehat {ICB}\)

Do đó \(\Delta BIC\) cân tại \(I\).

Bài 11: Cho \(\Delta ABC\) cân tại \(A\). Gọi \(M\) là trung điểm của \(BC\). Chứng minh \(AM\) vuông góc với \(BC\) và \(AM\) là tia phân giác của góc \(\widehat {BAC}\).

Phương pháp

Chứng minh \(\Delta AMB = \Delta AMC\) (c.c.c) suy ra

+) \(\widehat {AMB} = \widehat {AMC}\) (2 góc tương ứng), mà hai góc là hai góc kề bù nên \(\widehat {AMB} = \widehat {AMC} = 90^\circ \) nên \(AM \bot BC\).

+) \(\widehat {MAB} = \widehat {MAC}\) (2 góc tương ứng) nên \(AM\) là tia phân giác của góc \(\widehat {BAC}\).

Lời giải

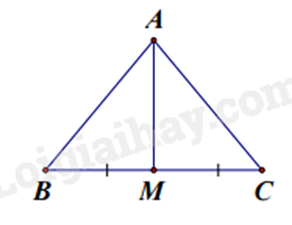
Xét \(\Delta AMB\) và \(\Delta AMC\) có:

\(AM\) cạnh chung

\(MB = MC\left( {gt} \right)\)

\(AB = AC\left( {gt} \right)\)

Do đó: \(\Delta AMB = \Delta AMC\) (c.c.c)

suy ra \(\widehat {AMB} = \widehat {AMC}\) (2 góc tương ứng)

Mà \(\widehat {AMB} + \widehat {AMC} = {180^ \circ }\) (2 góc kề bù)

nên \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = {90^ \circ }\)

hay \(AM \bot BC\)

Do \(\Delta AMB = \Delta AMC\left( {cmt} \right)\) nên \(\widehat {MAB} = \widehat {MAC}\) (2 góc tương ứng) hay \(AM\) là tia phân giác của góc \(\widehat {BAC}\).

Bài 12: Cho \(\Delta ABC\) cân tại \(A\). Lấy điểm \(D\) thuộc cạnh \(AC\), \(E\) thuộc cạnh \(AB\) sao cho \(AD = AE\).

a) Chứng minh \(BD = CE\)

b) Gọi \(I\) là giao điểm của \(BD\) và \(CE\). Chứng minh \(\Delta IBC\) và \(\Delta IED\) là các tam giác cân.

c) Chứng minh \(DE\parallel BC\).

Phương pháp

a) Chứng minh \(\Delta ADB = \Delta AEC\) (c.g.c) suy ra \(BD = CE\)

b) Vì \(\Delta ADB = \Delta AEC\) (cmt) nên \(\widehat {ABD} = \widehat {ACE}\) và \(\widehat {ADB} = \widehat {AEC}\)(2 cặp góc tương ứng)

Kết hợp với \(\widehat {BDC},\widehat {CEB}\) là góc kề bù của \(\widehat {ADB},\widehat {AEC}\) suy ra \(\widehat {BDC} = \widehat {CEB}\)

Chứng minh \(EB = DC\)

Từ đó chứng minh \(\Delta BIE = \Delta CID\) (g.c.g)

suy ra \(IB = IC\) và \(IE = ID\)

Nên các \(\Delta IBC\) và \(\Delta IED\) đều là tam giác cân.

c) Chứng minh \(\Delta AED\) cân tại \(A\), suy ra \(\widehat {{E_1}} = \widehat {{D_1}} = \frac{{{{180}^ \circ } - \hat A}}{2}\)

Kết hợp với \(\Delta ABC\) cân tại \(A\) nên \(\widehat {ABC} = \widehat {ACB} = \frac{{{{180}^ \circ } - \hat A}}{2}\)

Suy ra \(\widehat {{E_1}} = \widehat {ABC}\) là 2 góc ở vị trí đồng vị nên \(ED\parallel BC\).

Lời giải

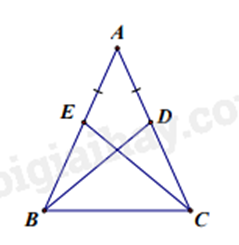
a) Xét \(\Delta ADB\) và \(\Delta AEC\) có:

\(AB = AC\) (gt)

\(\hat A\) góc chung

\(AD = AE\) (gt)

Do đó: \(\Delta ADB = \Delta AEC\) (c.g.c)

Suy ra \(BD = CE\)

b)

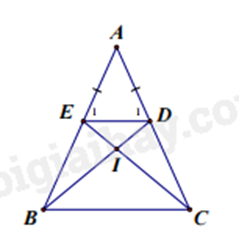
Vì \(\Delta ADB = \Delta AEC\) (cmt) nên \(\widehat {ABD} = \widehat {ACE}\) và \(\widehat {ADB} = \widehat {AEC}\)(2 cặp góc tương ứng) (1)

Mà \(\widehat {ADB} + \widehat {BDC} = {180^ \circ }\) (2 góc kề bù) (2)

và \(\widehat {AEC} + \widehat {CEB} = {180^ \circ }\) (2 góc kề bù) (3)

Từ (1), (2) và (3) suy ra \(\widehat {BDC} = \widehat {CEB}\)

Lại có: \(AB = AC\) (gt); \(AE = AD\) (gt) nên \(AB - AE = AC - AD\) hay \(EB = DC\)

Xét \(\Delta BIE\) và \(\Delta CID\) có:

\(\widehat {BEC} = \widehat {CDB}\) (cmt)

\(EB = DC\) (cmt)

\(\widehat {ABD} = \widehat {ACE}\) (cmt)

Do đó: \(\Delta BIE = \Delta CID\) (g.c.g)

suy ra \(IB = IC\) và \(IE = ID\)

Nên các \(\Delta IBC\) và \(\Delta IED\) đều là tam giác cân.

c) Ta có: \(AE = AD\) (gt) nên \(\Delta AED\) cân tại \(A\), suy ra \(\widehat {{E_1}} = \widehat {{D_1}} = \frac{{{{180}^ \circ } - \hat A}}{2}\) (4)

Mặt khác \(\Delta ABC\) cân tại \(A\) nên \(\widehat {ABC} = \widehat {ACB} = \frac{{{{180}^ \circ } - \hat A}}{2}\) (5)

Từ (4) và (5) suy ra \(\widehat {{E_1}} = \widehat {ABC}\).

Mà \(\widehat {{E_1}}\) và \(\widehat {ABC}\) là 2 góc ở vị trí đồng vị nên \(ED\parallel BC\).