Đề ôn hè Toán 7 lên 8 - Đề 4

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Chữ số thập phân thứ sáu của số \(0,2\left( {345} \right)\) là:

A. 5.

B. 4.

C. 3.

D. 2.

Câu 2: Kết quả của phép tính \(\sqrt {{5^2}}  - \left| { - 4} \right| + {2025^0}\) là:

A. 2.

B. 10.

C. 22.

D. 2026.

Câu 3: Từ năm 1997, Chính phủ Việt Nam quyết định lấy ngày 26/12 là ngày Dân số Việt Nam. Dân số của Việt Nam là 100 050 299 người vào ngày 27/12/2023 theo số liệu từ Liên Hợp Quốc.

(nguồn: https://danso.org/viet-nam/)

Làm tròn số dân này với độ chính xác 500, ta được kết quả là:

A. 100 050 300.

B. 100 000 000.

C. 100 100 000.

D. 100 050 000.

Câu 4: Cho hai đại lượng \(x\) và \(y\) liên hệ với nhau bởi công thức \(y = \frac{1}{3}x\). Khẳng định nào sau đây là đúng?

A. \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ 3.

B. \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(\frac{1}{3}\).

C. \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ 3.

D. \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(\frac{1}{3}\).

Câu 5: Hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác có chung đặc điểm nào dưới đây?

A. Có 6 mặt.

B. Có 8 đỉnh.

C. Có mặt đáy song song.

D. Mỗi đỉnh có 3 góc vuông.

Câu 6: Cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây là đúng?

A. Nếu a // b; b // c thì a \( \bot \) c.

B. Nếu a \( \bot \) b; b \( \bot \) c thì \(a\) \( \bot \) c.

C. Nếu a \( \bot \) b; b // c thì a // c.

D. Nếu a // b; b // c thì a // c.

Câu 7: Biểu đồ sau đây cho biết tỉ lệ học sinh tham giác các môn thể thao của học sinh khối 7 ở một trường THCS (mỗi học sinh chỉ tham gia 1 môn).

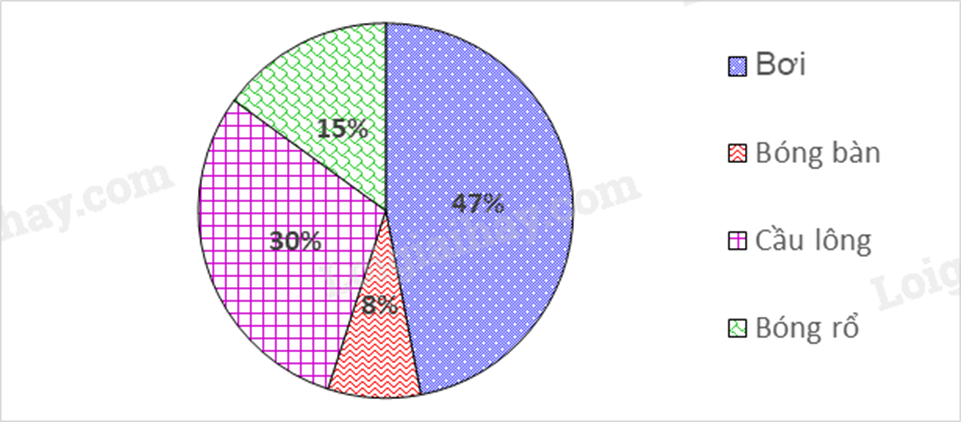
Môn thể thao có đông học sinh tham gia nhất là:

A. Bóng rổ.

B. Cầu lông.

C. Bóng bàn.

D. Bơi.

Câu 8: Gieo một con xúc xắc ngẫu nhiên một lần. Xác suất của biến cố “mặt xuất hiện có số chấm là số chẵn” là:

A. \(\frac{1}{3}\).

B. \(\frac{1}{6}\).

C. \(\frac{2}{3}\).

D. \(\frac{1}{2}\).

Phương pháp

Câu 9: Giá trị của biểu thức \(2x - 1\) tại \(x = 1\) là:

A. 1.

B. -4.

C. 2.

D. 0.

Câu 10: Đa thức \(3{x^2} + 4x + 1\) có bậc là:

A. 4.

B. 3.

C. 2.

D. 1.

Câu 11: Cho tam giác ABC vuông tại A có \(\widehat B = 60^\circ \). So sánh các cạnh của tam giác ABC, ta được:

A. AC > BC > AB.

B. BC > AC > AB.

C. AB > AC > BC.

D. BC > AB > AC.

Câu 12: Tam giác ABC (AB < AC) có M là trọng tâm. Khi đó M là giao điểm của

A. ba đường trung tuyến.

B. ba đường trung trực.

C. ba đường phân giác.

D. ba đường cao.

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm)

1. Thực hiện phép tính:

a) \( - \frac{3}{4} + {\left( { - 2025} \right)^0} + 0,75\).

b) \(\sqrt {\frac{{16}}{{49}}}  + \left| { - \frac{4}{7}} \right| - \frac{9}{7}.{\left( {\frac{{ - 1}}{3}} \right)^2} - 1\).

2. Tìm \(x\), biết: \(\frac{{\left| {x - 3} \right|}}{5} = \frac{1}{2}\)

Bài 2. (1 điểm) Cho hai đa thức:

\(A\left( x \right) = 9{x^4} + 2{x^2} - x + 6\);

\(B\left( x \right) =  - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}\).

a) Thu gọn và sắp xếp đa thức \(B\left( x \right)\) theo luỹ thừa giảm dần của biến.

b) Chứng tỏ \(x = 9\) là nghiệm của đa thức \(P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}\).

Bài 3. (1 điểm) Ba lớp 7A, 7B, 7C tham gia chương trình “Thu hồi pin để tái sinh” do nhà trường phát động. Biết rằng số viên pin thu được của các lớp đó theo thứ tự tỉ lệ với 3; 4; 5 và lớp 7C thu được nhiều hơn lớp 7A là 60 viên pin. Tính số viên pin thu được của mỗi lớp?

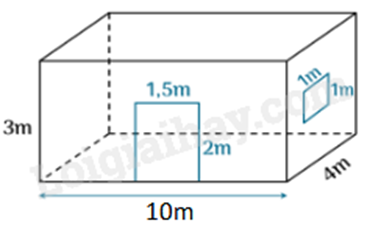
Bài 4. (1 điểm) Căn phòng nhà bạn An có một cửa lớn hình chữ nhật và một cửa sổ hình vuông với kích thước bên trong căn phòng (như hình vẽ). Bố bạn An cần trả bao nhiêu tiền để sơn bốn bức tường xung quanh bên trong căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông phải tốn 100 000 đồng (đã bao gồm tất cả các chi phí).

Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH (H \( \in \) BC). Tia phân giác của góc ABC cắt cạnh AC tại D. Trên cạnh BC lấy điểm M sao cho BM = BA.

a) Chứng minh \(\Delta ABD = \Delta MBD\) và \(DM \bot BC\).

b) Chứng minh \(\Delta DAM\) cân và AM là tia phân giác của góc HAC.

c) Chứng minh MC > MH.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Chữ số thập phân thứ sáu của số \(0,2\left( {345} \right)\) là:

A. 5.

B. 4.

C. 3.

D. 2.

Phương pháp

Viết chu kì của số dưới dạng đầy đủ để xác định chữ số thập phân thứ sáu.

Lời giải

Ta có: \(0,2\left( {345} \right) = 0,2345345...\) nên chữ số thập phân thứ sau của số là chữ số 4.

Đáp án: B.

Câu 2: Kết quả của phép tính \(\sqrt {{5^2}}  - \left| { - 4} \right| + {2025^0}\) là:

A. 2.

B. 10.

C. 22.

D. 2026.

Phương pháp

Tính căn bậc hai, giá trị tuyệt đối, luỹ thừa rồi tính phép tính.

Lời giải

Ta có: \(\sqrt {{5^2}}  - \left| { - 4} \right| + {2025^0} = 5 - 4 + 1 = 2\).

Đáp án: A.

Câu 3: Từ năm 1997, Chính phủ Việt Nam quyết định lấy ngày 26/12 là ngày Dân số Việt Nam. Dân số của Việt Nam là 100 050 299 người vào ngày 27/12/2023 theo số liệu từ Liên Hợp Quốc.

(nguồn: https://danso.org/viet-nam/)

Làm tròn số dân này với độ chính xác 500, ta được kết quả là:

A. 100 050 300.

B. 100 000 000.

C. 100 100 000.

D. 100 050 000.

Phương pháp

Sử dụng quy tắc làm tròn số: làm tròn với độ chính xác 500 là làm tròn đến hàng nghìn.

Lời giải

Vì 2 < 0 nên ta giữ nguyên chữ số hàng nghìn.

Số 100 050 299 làm tròn với độ chính xác 500 là 100 050 000.

Đáp án: D.

Câu 4: Cho hai đại lượng \(x\) và \(y\) liên hệ với nhau bởi công thức \(y = \frac{1}{3}x\). Khẳng định nào sau đây là đúng?

A. \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ 3.

B. \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(\frac{1}{3}\).

C. \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ 3.

D. \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(\frac{1}{3}\).

Phương pháp

Hai đại lượng \(x\) và \(y\) liên hệ với nhau theo công thức \(y = kx\) thì \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ k.

Lời giải

Hai đại lượng \(x\) và \(y\) liên hệ với nhau theo công thức \(y = \frac{1}{3}x\) thì \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(\frac{1}{3}\).

Đáp án: B.

Câu 5: Hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác có chung đặc điểm nào dưới đây?

A. Có 6 mặt.

B. Có 8 đỉnh.

C. Có mặt đáy song song.

D. Mỗi đỉnh có 3 góc vuông.

Phương pháp

Dựa vào đặc điểm của các hình.

Lời giải

Hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác đều có các mặt đáy song song.

Đáp án: C.

Câu 6: Cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây là đúng?

A. Nếu a // b; b // c thì a \( \bot \) c.

B. Nếu a \( \bot \) b; b \( \bot \) c thì \(a\) \( \bot \) c.

C. Nếu a \( \bot \) b; b // c thì a // c.

D. Nếu a // b; b // c thì a // c.

Phương pháp

Dựa vào tính chất hai đường thẳng song song: Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

Lời giải

Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

Nếu a // b; b // c thì a // c nên D đúng.

Đáp án: D.

Câu 7: Biểu đồ sau đây cho biết tỉ lệ học sinh tham giác các môn thể thao của học sinh khối 7 ở một trường THCS (mỗi học sinh chỉ tham gia 1 môn).

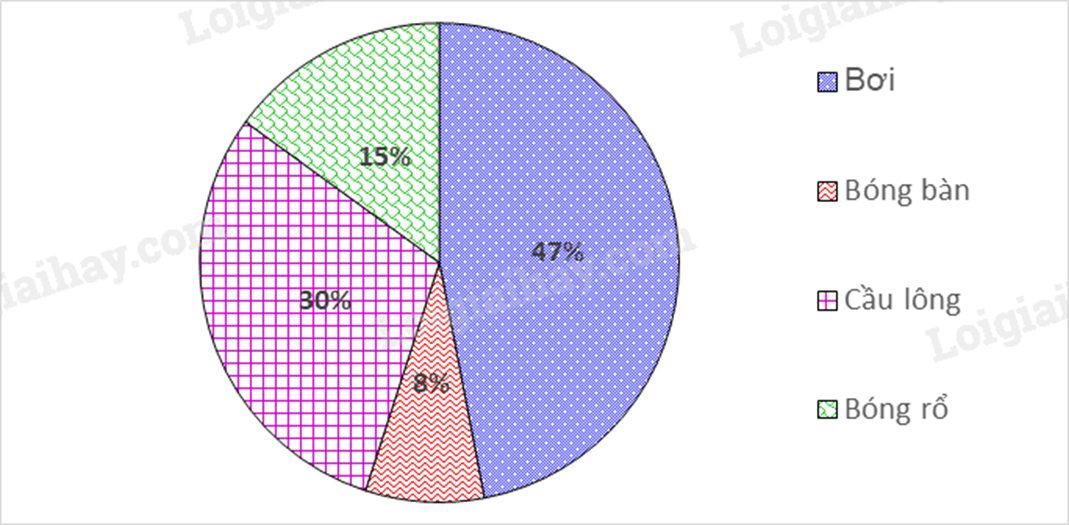
Môn thể thao có đông học sinh tham gia nhất là:

A. Bóng rổ.

B. Cầu lông.

C. Bóng bàn.

D. Bơi.

Phương pháp

Xác định môn thể thao có tỉ số phần trăm lớn nhất.

Lời giải

Vì 47% > 30% > 15% > 8% nên môn thể thao có đông học sinh tham gia nhất là Cầu lông

Đáp án: B.

Câu 8: Gieo một con xúc xắc ngẫu nhiên một lần. Xác suất của biến cố “mặt xuất hiện có số chấm là số chẵn” là:

A. \(\frac{1}{3}\).

B. \(\frac{1}{6}\).

C. \(\frac{2}{3}\).

D. \(\frac{1}{2}\).

Phương pháp

Biến cố ngẫu nhiên: Có k biến cố đồng khả năng và luôn xảy ra 1 trong k biến cố này thì xác suất của mỗi biến cố đó là \(\frac{1}{k}\).

Lời giải

Có 3 khả năng xảy ra biến cố “mặt xuất hiện có số chấm là số chẵn”, đó là: mặt 2 chấm, mặt 4 chấm, mặt 6 chấm”.

Có 3 khả năng xảy ra biến cố “mặt xuất hiện có số chấm là số lẻ”, dố là: mặt 1 chấm, mặt 3 chấm, mặt 5 chấm”.

Khi đó hai biến cố là hai biến cố đồng khả năng và luôn xảy ra 1 trong 2 biến cố này. Vậy xác suất của biến cố “mặt xuất hiện có số chấm là số chẵn” là \(\frac{1}{2}\).

Đáp án: D.

Câu 9: Giá trị của biểu thức \(2x - 1\) tại \(x = 1\) là:

A. 1.

B. -4.

C. 2.

D. 0.

Phương pháp

Thay \(x = 1\) vào biểu thức để tính giá trị của biểu thức.

Lời giải

Giá trị của biểu thức \(2x - 1\) tại \(x = 1\) là: \(2.1 - 1 = 1\).

Đáp án: A.

Câu 10: Đa thức \(3{x^2} + 4x + 1\) có bậc là:

A. 4.

B. 3.

C. 2.

D. 1.

Phương pháp

Bậc của đa thức là số mũ lớn nhất của biến.

Lời giải

Đa thức \(3{x^2} + 4x + 1\) có số mũ lớn nhất của biến \(x\) là 2 nên đa thức có bậc là 2.

Đáp án: C.

Câu 11: Cho tam giác ABC vuông tại A có \(\widehat B = 60^\circ \). So sánh các cạnh của tam giác ABC, ta được:

A. AC > BC > AB.

B. BC > AC > AB.

C. AB > AC > BC.

D. BC > AB > AC.

Phương pháp

Dựa vào mối quan hệ của góc và cạnh trong tam giác.

Lời giải

Xét tam giác ABC, ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(\widehat C = 180^\circ  - \widehat A - \widehat B\)

Mà tam giác ABC vuông tại A nên \(\widehat A = 90^\circ \) và \(\widehat B = 60^\circ \) (gt)

Suy ra \(\widehat C = 180^\circ  - 90^\circ  - 60^\circ  = 30^\circ \).

Vì \(\widehat A > \widehat B > \widehat C\) (do \(90^\circ  > 60^\circ  > 30^\circ \)) nên \(BC > AC > AB\).

Đáp án: B.

Câu 12: Tam giác ABC (AB < AC) có M là trọng tâm. Khi đó M là giao điểm của

A. ba đường trung tuyến.

B. ba đường trung trực.

C. ba đường phân giác.

D. ba đường cao.

Phương pháp

Dựa vào kiến thức về sự đồng quy của đường trung tuyến, trung trực, phân giác và đường cao.

Lời giải

M là trọng tâm của tam giác ABC nên M là giao điểm của ba đường trung tuyến của \(\Delta ABC\).

Đáp án: A.

Phần tự luận.

Bài 1. (1,5 điểm)

1. Thực hiện phép tính:

a) \( - \frac{3}{4} + {\left( { - 2025} \right)^0} + 0,75\).

b) \(\sqrt {\frac{{16}}{{49}}}  + \left| { - \frac{4}{7}} \right| - \frac{9}{7}.{\left( {\frac{{ - 1}}{3}} \right)^2} - 1\).

2. Tìm \(x\), biết: \(\frac{{\left| {x - 3} \right|}}{5} = \frac{1}{2}\)

Phương pháp

1. Thực hiện phép tính theo đúng thứ tự ưu tiên.

2. Thực hiện chuyển vế.

Nếu \(\left| A \right| = B\) (\(B > 0\)) thì \(A = B\) hoặc \(A =  - B\). Chia hai trường hợp để tìm \(x\).

Lời giải

1.

a) \( - \frac{3}{4} + {\left( { - 2025} \right)^0} + 0,75\)

\(\begin{array}{l} =  - \frac{3}{4} + 1 + \frac{3}{4}\\ = \left( { - \frac{3}{4} + \frac{3}{4}} \right) + 1\\ = 0 + 1\\ = 1\end{array}\)

b) \(\sqrt {\frac{{16}}{{49}}}  + \left| { - \frac{4}{7}} \right| - \frac{9}{7}.{\left( {\frac{{ - 1}}{3}} \right)^2} - 1\)

\(\begin{array}{l} = \frac{4}{7} + \frac{4}{7} - \frac{9}{7}.\frac{1}{9} - 1\\ = \frac{8}{7} - \frac{1}{7} - 1\\ = 1 - 1\\ = 0\end{array}\)

2. \(\frac{{\left| {x - 3} \right|}}{5} = \frac{1}{2}\)

\(\left| {x - 3} \right| = \frac{5}{2}\)

suy ra \(x - 3 = \frac{5}{2}\) hoặc \(x - 3 =  - \frac{5}{2}\).

TH1: \(x - 3 = \frac{5}{2}\)

          \(\begin{array}{l}x = \frac{5}{2} + 3\\x = \frac{{11}}{2}\end{array}\)

TH1: \(x - 3 =  - \frac{5}{2}\)

          \(\begin{array}{l}x =  - \frac{5}{2} + 3\\x = \frac{1}{2}\end{array}\)

Vậy \(x \in \left\{ {\frac{{11}}{2};\frac{1}{2}} \right\}\).

Bài 2. (1 điểm) Cho hai đa thức:

\(A\left( x \right) = 9{x^4} + 2{x^2} - x + 6\);

\(B\left( x \right) =  - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}\).

a) Thu gọn và sắp xếp đa thức \(B\left( x \right)\) theo luỹ thừa giảm dần của biến.

b) Chứng tỏ \(x = 9\) là nghiệm của đa thức \(P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}\).

Phương pháp

a) Bước 1: Cộng, trừ các đơn thức cùng bậc để thu được đa thức thu gọn không chứa hai đơn thức nào cùng bậc

Bước 2: Sắp xếp đa thức trên theo lũy thừa giảm của biến.

b) Tìm đa thức P(x).

Thay \(x = 9\) vào \(P\left( x \right)\), nếu \(P\left( 9 \right) = 0\) thì \(x = 9\) là nghiệm của \(P\left( x \right)\).

Lời giải

a) Ta có:

\(\begin{array}{l}B\left( x \right) =  - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}\\B\left( x \right) =  - 8{x^4} + \left( {4{x^3} - 5{x^3}} \right) - 2{x^2} + 3\\B\left( x \right) =  - 8{x^4} - {x^3} - 2{x^2} + 3\end{array}\)

b) Ta có:

\(\begin{array}{l}P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}\\P\left( x \right) = \left( {9{x^4} + 2{x^2} - x + 6} \right) + \left( { - 8{x^4} - {x^3} - 2{x^2} + 3} \right) - {x^4} + {x^3}\\P\left( x \right) = 9{x^4} + 2{x^2} - x + 6 - 8{x^4} - {x^3} - 2{x^2} + 3 - {x^4} + {x^3}\\P\left( x \right) = \left( {9{x^4} - 8{x^4} - {x^4}} \right) + \left( { - {x^3} + {x^3}} \right) + \left( {2{x^2} - 2{x^2}} \right) - x + \left( {6 + 3} \right)\\P\left( x \right) =  - x + 9\end{array}\)

Ta có: \(P\left( 9 \right) =  - 9 + 9 = 0\) nên \(x = 9\) là nghiệm của \(P\left( x \right)\).

Bài 3. (1 điểm) Ba lớp 7A, 7B, 7C tham gia chương trình “Thu hồi pin để tái sinh” do nhà trường phát động. Biết rằng số viên pin thu được của các lớp đó theo thứ tự tỉ lệ với 3; 4; 5 và lớp 7C thu được nhiều hơn lớp 7A là 60 viên pin. Tính số viên pin thu được của mỗi lớp?

Phương pháp

Gọi số viên pin mà ba lớp 7A, 7B, 7C thu được lần lượt là \(x,y,z\) (viên).

Dựa vào đề bài biểu diễn dãy tỉ số bằng nhau.

Áp dụng tính chất dãy tỉ số bằng nhau để tìm \(x,y,z\).

Lời giải

Gọi số viên pin mà ba lớp 7A, 7B, 7C thu được lần lượt là \(x,y,z\) (viên).

Vì số viên pin thu được của các lớp 7A, 7B, 7C theo thứ tự tỉ lệ với 3; 4; 5 nên ta có: \(\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\).

Lớp 7C thu được nhiều hơn lớp 7A là 60 viên pin nên ta có: \(z - x = 60\).

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{x}{3} = \frac{y}{4} = \frac{z}{5} = \frac{{z - x}}{{5 - 3}} = \frac{{60}}{2} = 30\).

Suy ra \(x = 30.3 = 90\);

            \(y = 30.4 = 120\);

            \(z = 30.5 = 150\).

Vậy số viên pin mà ba lớp 7A, 7B, 7C thu được lần lượt là 90 viên, 120 viên, 150 viên.

Bài 4. (1 điểm) Căn phòng nhà bạn An có một cửa lớn hình chữ nhật và một cửa sổ hình vuông với kích thước bên trong căn phòng (như hình vẽ). Bố bạn An cần trả bao nhiêu tiền để sơn bốn bức tường xung quanh bên trong căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông phải tốn 100 000 đồng (đã bao gồm tất cả các chi phí).

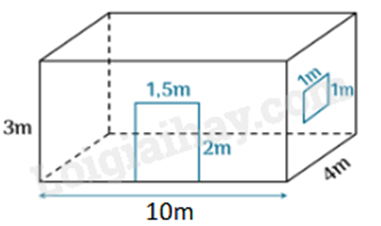
Phương pháp

Tính diện tích xung quanh của căn phòng.

Tính diện tích các cửa.

Diện tích sơn = diện tích xung quanh của căn phòng – diện tích các cửa.

Số tiền sơn = diện tích sơn . số tiền sơn mỗi mét vuông.

Lời giải

Diện tích xung quanh của căn phòng là: \(2\left( {10 + 4} \right).3 = 84\left( {{m^2}} \right)\)

Diện tích các cửa là: \(2.1,5 + 1.1 = 4\left( {{m^2}} \right)\)

Diện tích cần quét sơn là: \(84 - 4 = 80\left( {{m^2}} \right)\)

Bố An phải trả số tiền là: \(80.100\,000 = 8\,000\,000\) (đồng)

Vậy bố An phải trả số tiền là 8 000 000 đồng.

Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH (H \( \in \) BC). Tia phân giác của góc ABC cắt cạnh AC tại D. Trên cạnh BC lấy điểm M sao cho BM = BA.

a) Chứng minh \(\Delta ABD = \Delta MBD\) và \(DM \bot BC\).

b) Chứng minh \(\Delta DAM\) cân và AM là tia phân giác của góc HAC.

c) Chứng minh MC > MH.

Phương pháp

a) Chứng minh \(\Delta ABD = \Delta MBD\) (c.g.c)

* Suy ra hai góc tương ứng bằng nhau, suy ra \(DM \bot BC\).

b) * Chứng minh \(\Delta DAM\) có DA = DM nên cân tại D.

* Chứng minh AH // DM suy ra \(\widehat {HAM} = \widehat {AMD}\) (hai góc so le trong)

Vì \(\Delta DAM\) cân nên \(\widehat {MAD} = \widehat {AMD}\)

Do đó \(\widehat {HAM} = \widehat {MAD}\) hay \(\widehat {HAM} = \widehat {MAC}\) nên AM là tia phân giác của góc HAC.

c) Kẻ MK \( \bot \) AC tại K.

Chứng minh \(\Delta AHM = \Delta AKM\) (cạnh huyền – góc nhọn)

Do đó \(MH = MK\) (hai cạnh tương ứng).

Chứng minh MC > MK

Suy ra MC > MH.

Lời giải

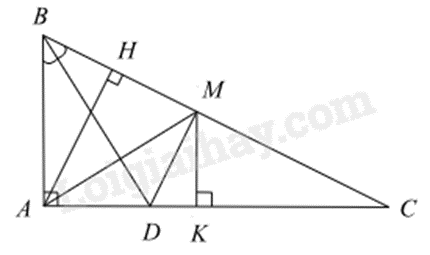
a) * Xét \(\Delta ABD\) và \(\Delta MBD\) có:

\(BA = BM\) (gt)

\(\widehat {ABD} = \widehat {MBD}\) (BD là tia phân giác của \(\widehat {ABM}\))

BD chung

Suy ra \(\Delta ABD = \Delta MBD\) (c.g.c)

* Suy ra \(\widehat {BAD} = \widehat {BMD} = 90^\circ \) (hai góc tương ứng), do đó \(DM \bot BM\) hay \(DM \bot BC\).

b) * Vì \(\Delta ABD = \Delta MBD\) (cmt) nên AD = DM, suy ra \(\Delta DAM\) cân tại D.

* Vì \(AH \bot BC,DM \bot BC\) nên AH // DM.

Suy ra \(\widehat {HAM} = \widehat {AMD}\) (hai góc so le trong)

Vì \(\Delta DAM\) cân tại D nên \(\widehat {MAD} = \widehat {AMD}\)

Do đó \(\widehat {HAM} = \widehat {MAD}\) hay \(\widehat {HAM} = \widehat {MAC}\) nên AM là tia phân giác của góc HAC.

c) Kẻ MK \( \bot \) AC tại K.

Xét \(\Delta AHM\) và \(\Delta AKM\) có:

\(\widehat {AHM} = \widehat {AKM}\left( { = 90^\circ } \right)\)

AM chung

\(\widehat {HAM} = \widehat {MAK}\) (AM là tia phân giác của \(\widehat {HAC}\))

Suy ra \(\Delta AHM = \Delta AKM\) (cạnh huyền – góc nhọn)

Do đó \(MH = MK\) (hai cạnh tương ứng).

Xét tam giác MKC vuông tại K nên MC > MK (cạnh huyền là cạnh lớn nhất trong tam giác)

Suy ra MC > MH.