Dạng bài góc và cạnh của một tam giác - Ôn hè Toán 7 lên 8

Lý thuyết

* Góc trong của tam giác:

Tổng ba góc của một tam giác bằng \(180^\circ \).

* Góc ngoài của tam giác:

- Định nghĩa: Góc ngoài của một tam giác là góc kề bù với một góc trong của tam giác ấy.

- Tính chất: Số đo góc ngoài bằng tổng hai góc trong không kề với nó.

* Góc đối diện với cạnh lớn hơn:

Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Trong tam giác ABC, nếu AC > AB thì \(\widehat B > \widehat C\).

* Cạnh đối diện với góc lớn hơn:

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trong tam giác ABC, nếu \(\widehat B > \widehat C\) thì AC > AB.

Nhận xét:

- Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

- Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

* Bất đẳng thức tam giác:

- Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

- Trong một tam giác, hiệu độ dài hai cạnh bất kì luôn nhỏ hơn độ dài cạnh còn lại.

Trong tam giác ABC, ta có:

\(\begin{array}{l}AB + AC > BC > \left| {AB - AC} \right|\\AB + BC > AC > \left| {AB - BC} \right|\\AC + BC > AB > \left| {AC - BC} \right|\end{array}\)

Bài tập

Bài 1: Cho tam giác ABC có \(\hat A = 86^\circ ;\hat B = 62^\circ \). Số đo góc C là:

A. \(32^\circ \).

B. \(35^\circ \).

C. \(24^\circ \).

D. \(90^\circ \).

Bài 2: Cho hình sau. Tính số đo x:

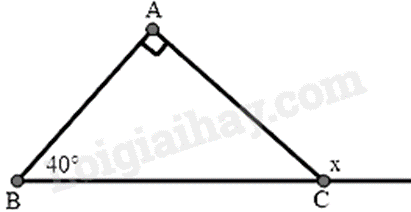
A. \(90^\circ \).

B. \(100^\circ \).

C. \(120^\circ \).

D. \(130^\circ \).

Bài 3: Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, câu nào đúng?

A. \(\hat A > \hat B > \hat C\).

B. \(\hat C > \hat A > \hat B\).

C. \(\hat C < \hat A < \hat B\).

D. \(\hat A < \hat B < \hat C\).

Bài 4: Cho tam giác ABC có \(\hat B = {90^0}\), \(\hat A = {35^0}\). Em hãy chọn câu trả lời đúng nhất.

A. \(BC < AB < AC\).

B. \(AC < AB < BC\).

C. \(AC < BC < AB\).

D. \(AB < BC < AC\).

Bài 5: Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. 

A. 3cm,5cm,7cm.

B. 4cm,5cm,6cm.

C. 2cm,5cm,7cm.

D. 3cm,6cm,5cm.

Bài 6: Cho tam giác ABC biết \(AB = 1cm\); \(BC = 6cm\) và cạnh AC là một số nguyên. Chu vi tam giác ABC là 

A. 17cm.

B. 15cm.

C. 13cm.

D. 16cm.

Bài 7: Cho hình vẽ sau. Tính số đo góc x:

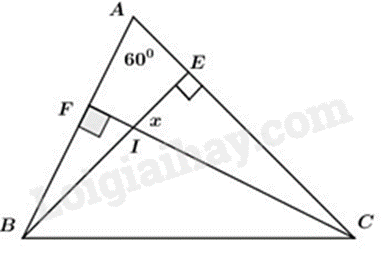
Bài 8: Cho tam giác ABC có \(\hat A = 50^\circ ,\hat B = 70^\circ \). Tia phân giác của góc C cắt cạnh AB tại M. Tính đo góc BMC.

Bài 9: Cho \(\Delta ABC\) có \(AB + AC = 10cm,AC - AB = 4cm\). So sánh \(\hat B\) và \(\hat C\)?

Bài 10: Cho tam giác ABC có \(\hat C > \hat B\) (\(\hat B,{\mkern 1mu} \hat C\) là các góc nhọn). Vẽ phân giác AD. So sánh BD và CD.

Bài 11: Tam giác ABC có \(\hat B + \hat C = \hat A\) và \(\hat C = 2\hat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\).

Bài 12: Cho tam giác ABC, biết \(\hat A:\hat B:\hat C = 3:5:7.\) So sánh các cạnh của tam giác.

Bài 13: Cho tam giác ABH vuông tại \(H{\mkern 1mu} \left( {\hat A > \hat B} \right).\) Kẻ đường cao \(HC{\mkern 1mu} {\mkern 1mu} \left( {C \in AB} \right).\) So sánh BH và \(AH;{\mkern 1mu} CH\) và CB.

Bài 14: Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng 5cm. Tính cạnh BC của tam giác đó biết chu vi của tam giác là 17cm.

Bài 15: Cho \(\Delta ABC\) có \(M\) là trung điểm BC. So sánh \(AB + AC\) và 2AM.

--------Hết--------

Lời giải chi tiết:

Bài 1: Cho tam giác ABC có \(\hat A = 86^\circ ;\hat B = 62^\circ \). Số đo góc C là:

A. \(32^\circ \).

B. \(35^\circ \).

C. \(24^\circ \).

D. \(90^\circ \).

Phương pháp

Tổng số đo 3 góc trong 1 tam giác bằng \(180^\circ \).

Lời giải

Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

\(\hat A + \hat B + \hat C = 180^\circ \)

hay \(86^\circ  + 62^\circ  + \hat C = 180^\circ \)

nên \(\hat C = 180^\circ  - 86^\circ  - 62^\circ  = 32^\circ \).

Đáp án: A

Bài 2: Cho hình sau. Tính số đo x:

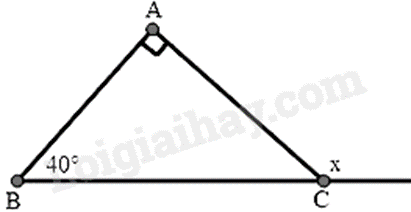
A. \(90^\circ \).

B. \(100^\circ \).

C. \(120^\circ \).

D. \(130^\circ \).

Phương pháp

Góc ngoài tam giác bằng tổng của hai góc trong không kề với nó.

Lời giải

Ta có góc cần tính là góc ngoài tại đỉnh C của tam giác ABC nên:

\(x = \hat A + \hat B = 90^\circ  + 40^\circ  = 130^\circ \)

Đáp án: D

Bài 3: Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, câu nào đúng?

A. \(\hat A > \hat B > \hat C\).

B. \(\hat C > \hat A > \hat B\).

C. \(\hat C < \hat A < \hat B\).

D. \(\hat A < \hat B < \hat C\).

Phương pháp

Áp dụng định lí: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Lời giải

Vì \(\Delta ABC\) có \(AC > BC > AB\) nên theo quan hệ giữa cạnh và góc trong tam giác ta có \(\hat B > \hat A > \hat C\) hay \(\hat C < \hat A < \hat B\).

Đáp án: C

Bài 4: Cho tam giác ABC có \(\hat B = {90^0}\), \(\hat A = {35^0}\). Em hãy chọn câu trả lời đúng nhất.

A. \(BC < AB < AC\).

B. \(AC < AB < BC\).

C. \(AC < BC < AB\).

D. \(AB < BC < AC\).

Phương pháp

- Tính \(\hat C\) và so sánh các góc của \(\Delta ABC\).

- Áp dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Lời giải

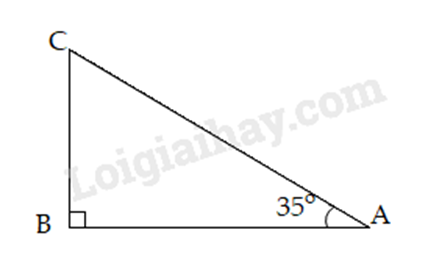
Xét \(\Delta ABC\) có:

\(\hat A + \hat B + \hat C = 180^\circ \) (định lý tổng ba góc trong tam giác)

suy ra \(\hat C = 180^\circ  - \hat A - \hat B = 180^\circ  - 35^\circ  - 90^\circ  = 55^\circ \)

suy ra \(\hat A < \hat C < \hat B\) suy ra \(BC < AB < AC\)

Đáp án: A

Bài 5: Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. 

A. 3cm,5cm,7cm.

B. 4cm,5cm,6cm.

C. 2cm,5cm,7cm.

D. 3cm,6cm,5cm.

Phương pháp

Ta kiểm tra tổng độ dài 2 đoạn thẳng ngắn hơn có lớn hơn độ dài đoạn thẳng dài nhất hay không. Nếu thỏa mãn thì 3 đoạn thẳng đã cho ghép được thành 1 tam giác.

Lời giải

+ Xét bộ ba: 3cm,5cm,7cm.

Ta có: \(3 + 5 = 8 > 7\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba 3cm,5cm,7cm lập thành một tam giác. Loại đáp án A.

+ Xét bộ ba: 4cm,5cm,6cm.

Ta có: \(4 + 5 = 9 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba 4cm,5cm,6cm lập thành một tam giác. Loại đáp án B.

+ Xét bộ ba: 2cm,5cm,7cm.

Ta có: \(2 + 5 = 7\) (không thỏa mãn bất đẳng thức tam giác) nên bộ ba 2cm,5cm,7cm không lập thành một tam giác. Chọn đáp án C.

+ Xét bộ ba: 3cm,5cm,6cm.

Ta có: \(3 + 5 = 8 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba 3cm,5cm,6cm lập thành một tam giác. Loại đáp án D.

Đáp án: C

Bài 6: Cho tam giác ABC biết \(AB = 1cm\); \(BC = 6cm\) và cạnh AC là một số nguyên. Chu vi tam giác ABC là 

A. 17cm.

B. 15cm.

C. 13cm.

D. 16cm.

Phương pháp

Áp dụng bất đẳng thức trong tam giác để tính cạnh AC.

Từ đó tính chu vi tam giác ABC.

Lời giải

Gọi độ dài cạnh AC là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:

\(6 - 1 < x < 6 + 1\)

\(5 < x < 7\).

Vì \(x\) là số nguyên nên \(x = 6.\)

Do đó độ dài cạnh \(AC = 6cm.\)

Chu vi tam giác ABC là \(AB + BC + AC = 1 + 6 + 6 = 13{\mkern 1mu} cm.\)

Đáp án: C

Bài 7: Cho hình vẽ sau. Tính số đo góc x:

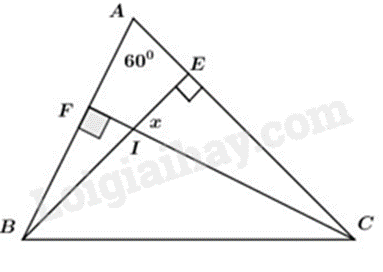
Phương pháp

Áp dụng định lí tổng ba góc của một tam giác bằng \(180^\circ \).

Lời giải

Áp dụng tính chất tổng ba góc trong tam giác ACF có:

\(\hat A + \widehat {ACF} + \widehat {AFC} = 180^\circ \)

hay \(60^\circ  + \widehat {ACF} + 90^\circ  = 180^\circ \)

suy ra \(\widehat {ACF} = 180^\circ  - 60^\circ  - 90^\circ  = 30^\circ .\)

Áp dụng tính chất tổng ba góc trong \(\Delta IEC\) ta có:

\(\widehat {IEC} + \widehat {ECI} + \widehat {EIC} = 180^\circ \)

hay \(30^\circ  + x + 90^\circ  = 180^\circ \)

suy ra \(x = 180^\circ  - 30^\circ  - 90^\circ  = 60^\circ .\)

Bài 8: Cho tam giác ABC có \(\hat A = 50^\circ ,\hat B = 70^\circ \). Tia phân giác của góc C cắt cạnh AB tại M. Tính đo góc BMC.

Phương pháp

Áp dụng định lí tổng ba góc của một tam giác, tính chất tia phân giác của một góc.

Lời giải

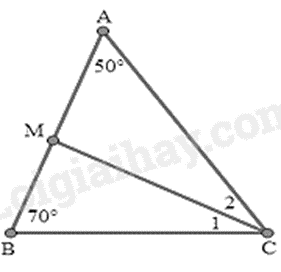
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

\(\hat A + \hat B + \hat C = 180^\circ \)

suy ra \(\hat C = 180^\circ  - \left( {\hat A + \hat B} \right)\)

\( = 180^\circ  - \left( {50^\circ  + 70^\circ } \right) = 60^\circ \).

Do CM là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\hat C}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).

Áp dụng định lí tổng ba góc trong tam giác BMC có:

\(\hat B + \widehat {BMC} + {\hat C_1} = 180^\circ \)

suy ra \(\widehat {BMC} = 180^\circ  - \left( {\hat B + \widehat {{C_1}}} \right)\)

\( = 180^\circ  - \left( {70^\circ  + 30^\circ } \right) = 80^\circ \)

Bài 9: Cho \(\Delta ABC\) có \(AB + AC = 10cm,AC - AB = 4cm\). So sánh \(\hat B\) và \(\hat C\)?

Phương pháp

 - Tính và so sánh độ dài các cạnh của tam giác.

- Áp dụng định lí: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn

Lời giải

Xét \(\Delta ABC\) có:

AB + AC = 10cm (1) và AC - AB = 4cm (2)

nên AB = \(\frac{{10 - 4}}{2}\) = 3 (cm)

suy ra AC = 10 - 3 = 7 (cm)

Do đó AC > AB suy ra \(\widehat B > \widehat C\).

Bài 10: Cho tam giác ABC có \(\hat C > \hat B\) (\(\hat B,{\mkern 1mu} \hat C\) là các góc nhọn). Vẽ phân giác AD. So sánh BD và CD.

Phương pháp

+ Trên cạnh AB lấy điểm E sao cho AC = AE.

+ So sánh CD với DE bằng cách sử dụng hai tam giác bằng nhau

+ So sánh DE với BC theo quan hệ giữa cạnh và góc trong tam giác

+ Từ đó so sánh CD và BD.

Lời giải

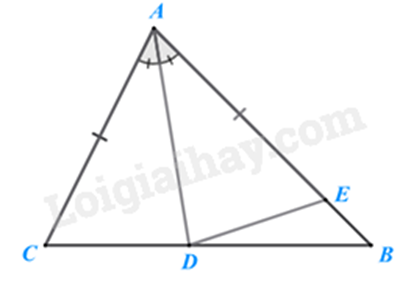
Từ đề bài \(\hat C > \hat B\) nên \(AB > AC\). Trên cạnh AB lấy điểm \(E\) sao cho \(AC = AE.\)

Xét tam giác ACD và tam giác AED có

+ \(AC = AE\)

+ \(\widehat {CAD} = \widehat {DAB}\) (tính chất tia phân giác)

+ Cạnh AD chung

nên \(\Delta ACD = \Delta AED\left( {c - g - c} \right)\)

suy ra \(DE = CD{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\) và \(\widehat {AED} = \widehat {ACD}\)

Mà \(\widehat {ACD}\) là góc nhọn nên \(\widehat {AED}\) là góc nhọn, suy ra \(\widehat {BED} = 180^\circ  - \widehat {AED}\) là góc tù, do đó \(\widehat {BED} > \widehat {EBD}\)

Xét tam giác BED có \(\widehat {BED} > \widehat {EBD}\) suy ra \(BD > DE{\mkern 1mu} {\mkern 1mu} \left( 2 \right)\)

Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(DC < BD.\)

Bài 11: Tam giác ABC có \(\hat B + \hat C = \hat A\) và \(\hat C = 2\hat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\).

Phương pháp

Sử dụng định lí tổng các góc của một tam giác, tính chất tia phân giác của một góc.

Lời giải

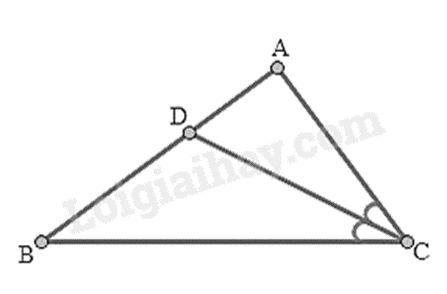
Xét tam giác ABC có \(\hat A + \hat B + \hat C = 180^\circ \) mà \(\hat B + \hat C = \hat A\), do đó \(2\hat A = 180^\circ \) suy ra \(\hat A = 90^\circ \).

Xét tam giác ABC có \(\hat A = 90^\circ \) nên \(\hat B + \hat C = 90^\circ \).

Mà \(\hat C = 2\hat B\) do đó \(3\hat B = 90^\circ \) suy ra \(\hat B = 30^\circ \) nên \(\hat C = 60^\circ \)

Do CD là tia phân giác của góc ACD nên \(\widehat {ACD} = \widehat {DCB} = \hat C:2 = 60^\circ :2 = 30^\circ \)

Xét tam giác ADC có:

\(\hat A + \widehat {ADC} + \widehat {ACD} = 180^\circ \) suy ra \(\widehat {ADC} = 180^\circ  - \left( {\hat A + \widehat {ACD}} \right) = 180^\circ  - \left( {30^\circ  + 90^\circ } \right) = 60^\circ \)

Bài 12: Cho tam giác ABC, biết \(\hat A:\hat B:\hat C = 3:5:7.\) So sánh các cạnh của tam giác.

Phương pháp

- Từ tỉ lệ góc cho trước ta so sánh các góc

- Sử dụng quan hệ giữa cạnh và góc trong tam giác để so sánh các cạnh.

Lời giải

Từ đề bài ta có \(\hat A:\hat B:\hat C = 3:5:7\) nên \(\frac{{\hat A}}{3} = \frac{{\hat B}}{5} = \frac{{\hat C}}{7}\)

suy ra \(\hat A < \hat B < \hat C\)

Vì \(\hat A < \hat B < \hat C\) nên \(BC < AC < AB.\)

Bài 13: Cho tam giác ABH vuông tại \(H{\mkern 1mu} \left( {\hat A > \hat B} \right).\) Kẻ đường cao \(HC{\mkern 1mu} {\mkern 1mu} \left( {C \in AB} \right).\) So sánh BH và \(AH;{\mkern 1mu} CH\) và CB.

Phương pháp

- Áp dụng:

+ Định lí: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

+ Định lí: Trong tam giác vuông, hai góc nhọn phụ nhau.

Lời giải

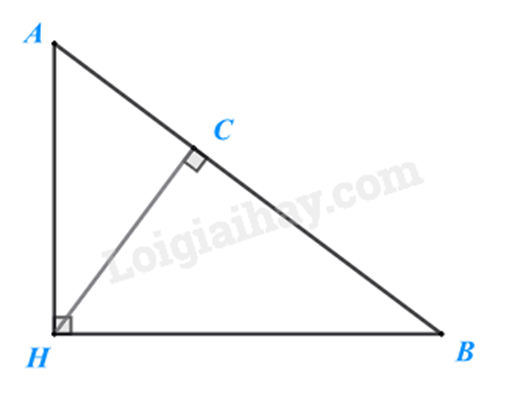
\(\Delta ABH\) có  (gt) nên \(BH > AH\) (quan hệ giữa góc và cạnh đối diện trong tam giác).

\(\Delta ABH\) vuông tại \(H\) nên \(\hat A + \hat B = 90^\circ \)        (1)

\(\Delta BCH\) vuông tại \(C\) nên \(\widehat {BHC} + \hat B = 90^\circ \)     (2)

Từ (1) và (2) suy ra \(\hat A = \widehat {BHC}\).

Mặt khác \(\widehat A > \widehat B\) (gt) nên \(\widehat {BHC} > \widehat B\) suy ra \(CB > CH\) (quan hệ giữa góc và cạnh đối diện trong tam giác).

Bài 14: Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng 5cm. Tính cạnh BC của tam giác đó biết chu vi của tam giác là 17cm.

Phương pháp

 - Áp dụng tính chất tam giác cân.

- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Lời giải

Giả sử \(\Delta ABC\) cân tại A.

- Trường hợp 1:

\(AB = AC = 5cm\) thì \(BC = 17 - 5 - 5 = 7cm.\)

Ta có: \(AB + AC = 5 + 5 = 10 > BC = 7cm\) (thỏa mãn bất đẳng thức tam giác)

- Trường hợp 2: \(BC = 5cm\) thì \(AB = AC = \left( {17 - 5} \right):2 = 6cm\)

Ta có: \(AB + BC = 5 + 6 = 11 > AC = 6cm\) (thỏa mãn bất đẳng thức tam giác)

Vậy nếu \(\Delta ABC\) cân tại A có:

+ \(AB = AC = 5cm\) thì \(BC = 7cm\)

+ \(BC = 5cm\) thì \(AB = AC = 6cm\)

Vậy \(BC = 7{\mkern 1mu} cm\) hoặc \(BC = 5{\mkern 1mu} cm.\)

Bài 15: Cho \(\Delta ABC\) có \(M\) là trung điểm BC. So sánh \(AB + AC\) và 2AM.

Phương pháp

- Trên tia đối của tia MA lấy điểm N sao cho MN = MA.

- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Lời giải

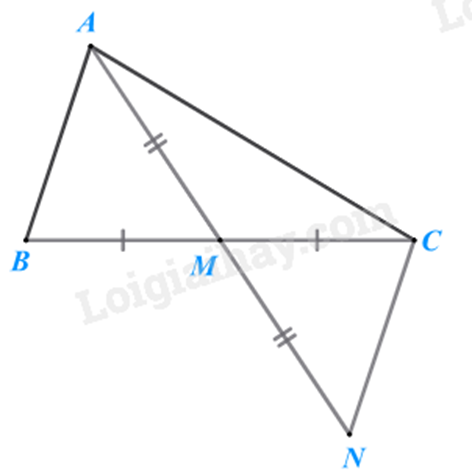
Trên tia đối của tia MA lấy điểm \(N\) sao cho \(MN = MA.\)

Vì M là trung điểm của BC (gt) nên MB = MC (tính chất trung điểm)

Xét \(\Delta MAB\) và \(\Delta MNC\) có:

\(MB = MC\left( {cmt} \right)\)

\(\widehat {AMB} = \widehat {NMC}\) (đối đỉnh)

\(AM = MN\left( {gt} \right)\)

nên \(\Delta MAB = \Delta MNC\left( {c - g - c} \right)\)

suy ra \(NC = AB\left( 1 \right)\) (2 cạnh tương ứng)

Xét \(\Delta ACN\) có: \(AN < AC + CN\left( 2 \right)\) (bất đẳng thức tam giác)

Từ \(\left( 1 \right)\left( 2 \right)\) suy ra \(AN < AC + AB\).

Mặt khác, \(AN = 2AM\left( {gt} \right)\) nên \(2AM < AB + AC.\)