Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
Tải vềDạng 1. Hình hộp chữ nhật và hình lập phương
Lý thuyết
|
|
Hình hộp chữ nhật
|
Hình lập phương
|
|
Đặc điểm |
- 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo. - Các mặt đều là hình chữ nhật. - Các cạnh bên bằng nhau. |
- 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo. - Các mặt đều là hình vuông. - Các cạnh đều bằng nhau. |
|
Diện tích xung quanh |
\({S_{xq}} = 2\left( {a + b} \right).h\) |
\({S_{xq}} = 4{a^2}\) |
|
Diện tích toàn phần |
\({S_{tp}} = {S_{xq}} + \) S2 đáy \( = 2\left( {a + b} \right).h + 2ab\) |
\({S_{tp}} = 6{a^2}\) |
|
Thể tích |
\(V = a.b.h\) |
\(V = {a^3}\) |
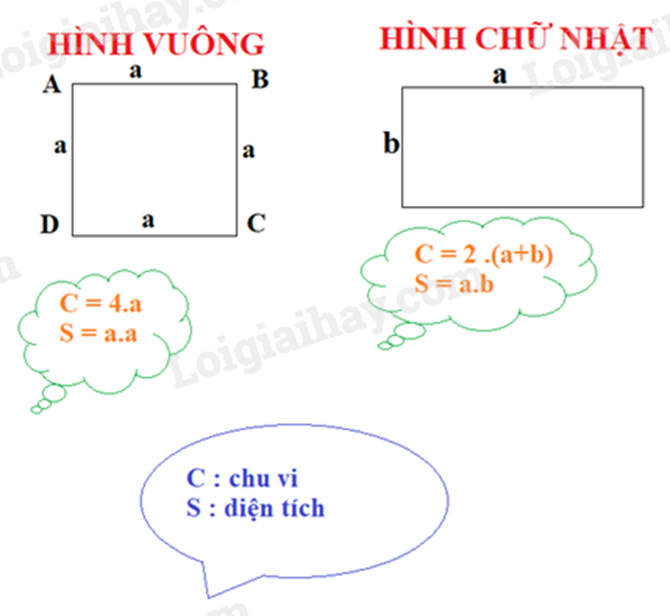
Lưu ý: Một số công thức tính chu vi và diện tích hình học liên quan:
Bài tập
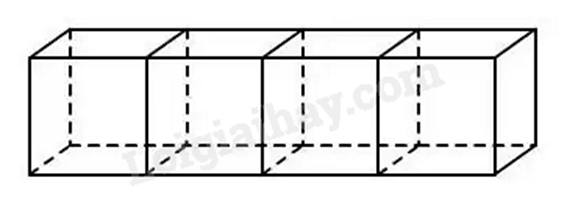
Bài 1: Trong hình dưới đây có m hình lập phương, n hình hộp chữ nhật. Tính m + n = ?
A. 8.
B. 9.
C. 10.
D. 11.
Bài 2: Hình hộp chữ nhật có
A. 4 mặt, 8 đỉnh, 12 cạnh.
B. 6 mặt, 8 đỉnh, 12 cạnh.
C. 6 mặt, 12 đỉnh, 8 cạnh.
D. 8 mặt, 6 đỉnh, 12 cạnh.
Bài 3: Cho hình lập phương ABCD.A'B'C'D'. Phát biểu nào sau đây là đúng?
A. 6 mặt là hình chữ nhật.
B. 6 mặt là hình vuông.
C. 6 mặt là hình thoi.
D. 8 mặt là hình vuông.
Bài 4: Chọn câu sai.
A. Hình hộp chữ nhật và hình lập phương có 6 mặt đều là hình vuông.
B. Hình hộp chữ nhật và hình lập phương đều có 8 đỉnh, 6 mặt và 12 cạnh.
C. Hình hộp chữ nhật và hình lập phương đều có 4 cạnh bên bằng nhau.
D. 8 mặt là hình vuông.
Bài 5: Hình hộp chữ nhật với ba kích thước lần lượt là a, 2a, 4a thì có thể tích là
A. a3 (đvtt).
B. 2a3 (đvtt).
C. 8a3 (đvtt).
D. 8a2 (đvdt).
Bài 6: Cho hình hộp chữ nhật có chiều dài bằng 6cm, chiều rộng bằng \(\frac{1}{3}\) chiều dài và chiều cao gấp 4 lần chiều rộng. Thể tích của hình hộp chữ nhật đó là
A. \(216c{m^3}\).
B. \(81c{m^3}\).
C. 288\(c{m^3}\).
D. 96\(c{m^3}\).
Bài 7: Cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh hình lập phương là 4 cm. Hỏi thể tích hình lập phương là bao nhiêu?
A. 16 cm3.
B. 4 cm3.
C. 32 cm3.
D. 64 cm3.
Bài 8: Bạn An làm một chiếc hộp đựng quà hình lập phương có cạnh bằng 10 cm. Bỏ qua các mép gấp, diện tích giấy mà bạn An cần dùng là

A. \(60c{m^2}\).
B. \(100c{m^2}\).
C. \(600c{m^2}\).
D. \(1000c{m^2}\).
Bài 9: Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 50 cm. Mực nước trong bể cao 25 cm. Người ta cho vào bể một hòn đá có thể tích tăng 20000 cm3. Hỏi mực nước trong bể lúc này cao bao nhiêu?
Bài 10: Một người thuê sơn mặt trong và mặt ngoài của 1 cái thùng sắt không nắp dạng hình lập phương có cạnh 0,8 m. Biết giá tiền mỗi mét vuông là 16000 đồng. Hỏi người ấy phải trả bao nhiêu tiền?
Bài 11: Một xưởng sản xuất đồ nội thất muốn sản xuất tủ quần áo có kích thước như hình vẽ.

Tính diện tích gỗ xưởng cần dùng để làm một chiếc tủ như thiết kế đó (giả sử độ dày của gỗ không đáng kể).
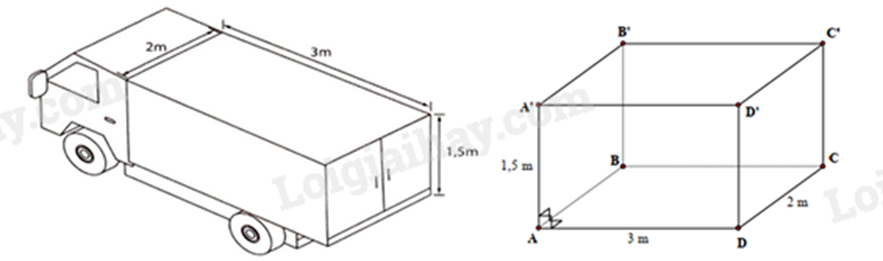
Bài 12: Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên. Tính thể tích của thùng xe và diện tích phần Inox đóng thùng xe (tính luôn sàn).
Bài 13: Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 1690 cm2. Tính thể tích của hình lập phương đó.
Bài 14: Một hình lăng trụ đứng có đáy là hình chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng 6cm. Một kích thước của đáy bằng 10cm, tính kích thước còn lại.
Bài 15: Một nhóm thợ xây có 100 khối bê tông có dạng như hình dưới đây.
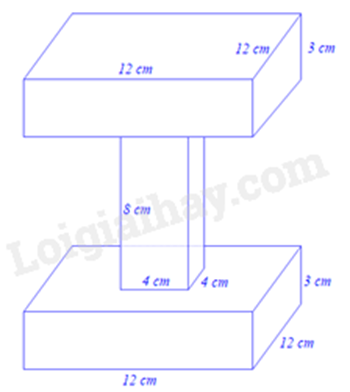
Người ta muốn sơn tất cả các mặt của từng khối bê tông. Hỏi số tiền sơn số bê tông đó là bao nhiêu đồng? Biết rằng số tiền để sơn 1 m2 bê tông là 100 000 đồng.
--------Hết--------
Lời giải chi tiết:
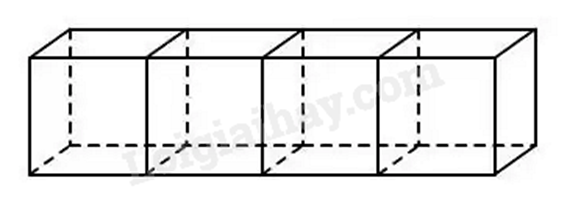
Bài 1: Trong hình dưới đây có m hình lập phương, n hình hộp chữ nhật. Tính m + n = ?
A. 8.
B. 9.
C. 10.
D. 11.
Phương pháp
Xác định số hình lập phương và số hình hộp chữ nhật có trong hình.
Lời giải
Hình trên có 4 hình lập phương và 6 hình hộp chữ nhật.
Vậy m = 4, n = 6.
Do đó, m + n = 4 + 6 = 10
Đáp án: C
Bài 2: Hình hộp chữ nhật có
A. 4 mặt, 8 đỉnh, 12 cạnh.
B. 6 mặt, 8 đỉnh, 12 cạnh.
C. 6 mặt, 12 đỉnh, 8 cạnh.
D. 8 mặt, 6 đỉnh, 12 cạnh.
Phương pháp
Đặc điểm của hình hộp chữ nhật.
Lời giải
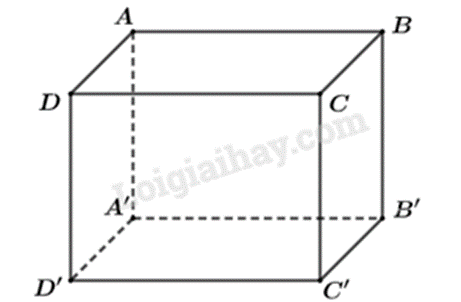
Quan sát hình vẽ, hình hộp chữ nhật ABCD.A'B'C'D' có:
+ 6 mặt: ABCD, A'B'C'D', ADD'A',BCC'B', ABB'A', DCD'C'
+ 8 đỉnh: A, B, C, D, A', B', C', D'
+ 12 cạnh: AB, A'B', BC, B'C', CD, C'D', DA,D'A', AA', BB', CC', DD'
Vậy hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
Đáp án: B
Bài 3: Cho hình lập phương ABCD.A'B'C'D'. Phát biểu nào sau đây là đúng?
A. 6 mặt là hình chữ nhật.
B. 6 mặt là hình vuông.
C. 6 mặt là hình thoi.
D. 8 mặt là hình vuông.
Phương pháp
Đặc điểm của hình lập phương.
Lời giải
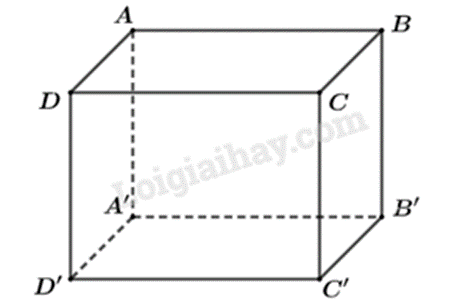
Hình lập phương có 6 mặt là hình vuông bằng nhau.
Đáp án: B
Bài 4: Chọn câu sai.
A. Hình hộp chữ nhật và hình lập phương có 6 mặt đều là hình vuông.
B. Hình hộp chữ nhật và hình lập phương đều có 8 đỉnh, 6 mặt và 12 cạnh.
C. Hình hộp chữ nhật và hình lập phương đều có 4 cạnh bên bằng nhau.
D. 8 mặt là hình vuông.
Phương pháp
Hình hộp chữ nhật là hình:
- Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình chữ nhật.
- Các cạnh bên bằng nhau.
Hình lập phương là hình:
- Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo
- Các mặt đều là hình vuông
- Các cạnh đều bằng nhau
Lời giải
Đáp án A sai vì hình hộp chữ nhật có 6 mặt là hình chữ nhật, hình lập phương có 6 mặt là hình vuông.
Đáp án: A
Bài 5: Hình hộp chữ nhật với ba kích thước lần lượt là a, 2a, 4a thì có thể tích là
A. a3 (đvtt).
B. 2a3 (đvtt).
C. 8a3 (đvtt).
D. 8a2 (đvdt).
Phương pháp
Thể tích hình hộp chữ nhật: V = chiều dài . chiều rộng . chiều cao
Lời giải
V = a. 2a. 4a = 8a3 (đvtt)
Đáp án: C
Bài 6: Cho hình hộp chữ nhật có chiều dài bằng 6cm, chiều rộng bằng \(\frac{1}{3}\) chiều dài và chiều cao gấp 4 lần chiều rộng. Thể tích của hình hộp chữ nhật đó là
A. \(216c{m^3}\).
B. \(81c{m^3}\).
C. 288\(c{m^3}\).
D. 96\(c{m^3}\).
Phương pháp
Tính độ dài chiều rộng và chiều cao của hình hộp
Thể tích hình hộp chữ nhật: V = chiều dài . chiều rộng . chiều cao
Lời giải
Chiều rộng của hình hộp chữ nhật là: \(6.\frac{1}{3} = 2{\mkern 1mu} \left( {cm} \right)\)
Chiều cao của hình hộp chữ nhật là: 4 . 2 = 8 ( cm)
Thể tích của hình hộp chữ nhật là: 6 . 2 . 8 = 96 ( cm3)
Đáp án: D
Bài 7: Cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh hình lập phương là 4 cm. Hỏi thể tích hình lập phương là bao nhiêu?
A. 16 cm3.
B. 4 cm3.
C. 32 cm3.
D. 64 cm3.
Phương pháp
Thể tích hình lập phương cạnh a là V = a3
Lời giải
Thể tích hình lập phương đó là:
V = 43 = 64 (cm3)
Đáp án: D
Bài 8: Bạn An làm một chiếc hộp đựng quà hình lập phương có cạnh bằng 10 cm. Bỏ qua các mép gấp, diện tích giấy mà bạn An cần dùng là

A. \(60c{m^2}\).
B. \(100c{m^2}\).
C. \(600c{m^2}\).
D. \(1000c{m^2}\).
Phương pháp
Diện tích giấy mà bạn An cần dùng chính là diện tích toàn phần của hình lập phương.
Diện tích toàn phần của hình lập phương bằng \(6{a^2}\) (với a là cạnh của hình lập phương).
Lời giải
Diện tích giấy mà bạn An cần dùng chính là diện tích toàn phần của hình lập phương.
Diện tích giấy mà bạn An cần dùng là: \({6.10^2} = 600\left( {c{m^2}} \right)\)
Đáp án: C
Bài 9: Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 50 cm. Mực nước trong bể cao 25 cm. Người ta cho vào bể một hòn đá có thể tích tăng 20000 cm3. Hỏi mực nước trong bể lúc này cao bao nhiêu?
Phương pháp
Tính thể tích nước ban đầu.
Tính thể tích phần bể chứa nước lúc sau.
Tính chiều cao mực nước lúc sau.
Lời giải
Thể tích phần bể chứa nước ban đầu là:
\(V = 80.50.25 = 100000\;c{m^3}\)
Sau khi cho vào một hòn đá thể tích tăng 20000 cm3.
Vậy thể tích phần bể chứa nước lúc sau là:
\({V_1} = V + 20000 = 100000 + 20000 = 120000\;c{m^3}\)
Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi.
Gọi chiều cao mực nước lúc sau là h cm. Ta có:
\(V = 80.50.h = 120000\) suy ra \(h = \frac{V}{{80.50}} = \frac{{120000}}{{80.50}} = 30\;cm\)
Bài 10: Một người thuê sơn mặt trong và mặt ngoài của 1 cái thùng sắt không nắp dạng hình lập phương có cạnh 0,8 m. Biết giá tiền mỗi mét vuông là 16000 đồng. Hỏi người ấy phải trả bao nhiêu tiền?
Phương pháp
Tính diện tích phần cần sơn.
Tính tiền = diện tích cần sơn . giá tiền.
Lời giải
Thùng sắt (không nắp) có dạng hình lập phương.\( \Rightarrow \)Thùng sắt có 5 mặt bằng nhau.
Diện tích một mặt thùng sắt là:
\(S = 0,{8^2} = 0,64\;{m^2}\)
Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt.
Vậy diện tích mặt trong và mặt ngoài thùng sắt là:
\({S_{mt}} = {S_{mn}} = 5S = 5.0,64 = 3,2\;{m^2}\)
Số tiền người thuê sơn thùng sắt cần trả là:
\(({S_{mt}} + {S_{mn}}).16000 = (3,2 + 3,2).16000 = 6,4.16000 = 102400\) (đồng)
Bài 11: Một xưởng sản xuất đồ nội thất muốn sản xuất tủ quần áo có kích thước như hình vẽ.

Tính diện tích gỗ xưởng cần dùng để làm một chiếc tủ như thiết kế đó (giả sử độ dày của gỗ không đáng kể).
Phương pháp
Diện tích toàn phần của hình hộp chữ nhật bằng diện tích xung quanh cộng với diện tích hai đáy.
Diện tích xung quanh của hình hộp chữ nhật bằng chu vi đáy nhân với chiều cao.
Lời giải
Đổi \(55{\mkern 1mu} cm = 0,55{\mkern 1mu} m\).
Diện tích xung quanh của chiếc tủ hình hộp chữ nhật là:
\(2\left( {1 + 0,55} \right).1,8 = 5,58{\mkern 1mu} \left( {{m^2}} \right)\)
Diện tích một mặt đáy của chiếc tủ là: \(0,55.1 = 0,55{\mkern 1mu} \left( {{m^2}} \right)\)
Diện tích hai mặt đáy của chiếc tủ là: \(0,55.2 = 1,1{\mkern 1mu} \left( {{m^2}} \right)\)
Tổng diện tích gỗ xưởng cần dùng để làm một chiếc tủ là: \(5,58 + 1,1 = 6,68{\mkern 1mu} {m^2}\)
Mà \(6,68{\mkern 1mu} {m^2} \approx 6,9{\mkern 1mu} {m^2}\)
Vậy diện tích gỗ cần dùng là \(6,9{\mkern 1mu} {m^2}\).
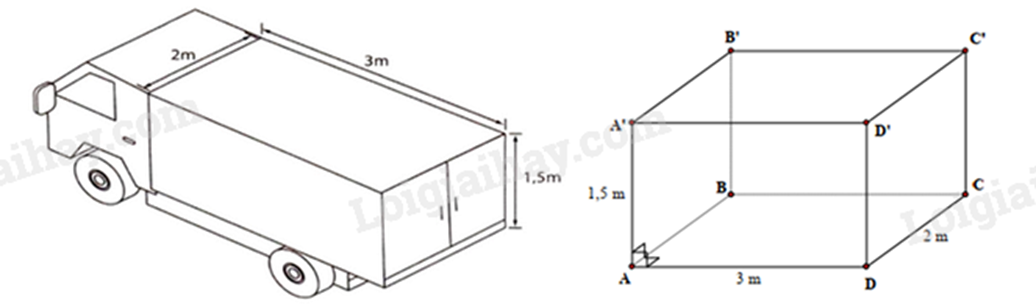
Bài 12: Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên. Tính thể tích của thùng xe và diện tích phần Inox đóng thùng xe (tính luôn sàn).
Phương pháp
- Sử dụng công thức tính thể tích hình hộp chữ nhật: V = chiều dài. chiều rộng. chiều cao.
- Diện tích phần Inox đóng thùng xe chính là diện tích toàn phần của hình hộp chữ nhật.
Stp = Sxq + 2Sđáy.
Sxq = chu vi đáy. chiều cao.
Lời giải
Thể tích thùng xe là: \(3.2.1,5 = 9\left( {{m^3}} \right)\).
Diện tích xung quanh Inox đóng thùng xe là: \(2\left( {3 + 2} \right).1,5 = 15\left( {{m^2}} \right)\).
Diện tích toàn phần Inox đóng thùng xe là: \(15 + 2.3.2 = 27\left( {{m^2}} \right)\).
Vậy thể tích thùng xe là \(9{m^3}\), diện tích phần Inox đóng thùng xe là \(27{m^2}\).
Bài 13: Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 1690 cm2. Tính thể tích của hình lập phương đó.
Phương pháp
+ Từ các điều kiện đề bài tìm cạnh của hình lập phương.
+ Sử dụng công thức thể tích hình lập phương để tính toán.
Lời giải
Chiếc hộp hình lập phương không nắp gồm 5 hình vuông, mỗi hình vuông được sơn 2 mặt nên số mặt là: 5.2 = 10 (hình vuông)
Do đó diện tích mỗi hình vuông là:
\(1690:10 = 169(c{m^2})\)
Ta có: \(169 = {13^2}\)
Vì diện tích hình vuông bằng bình phương một cạnh nên cạnh của hình lập phương bằng 13cm.
Thể tích của hình lập phương là:
\({13^3} = 2197(c{m^3})\)
Bài 14: Một hình lăng trụ đứng có đáy là hình chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng 6cm. Một kích thước của đáy bằng 10cm, tính kích thước còn lại.
Phương pháp
Sử dụng công thức diện tích xung quanh của hình lăng trụ đứng:
\({S_{xq}} = C.h\)
Trong đó, \(C\) là chu vi đáy; \(h\) là chiều cao.
Lời giải
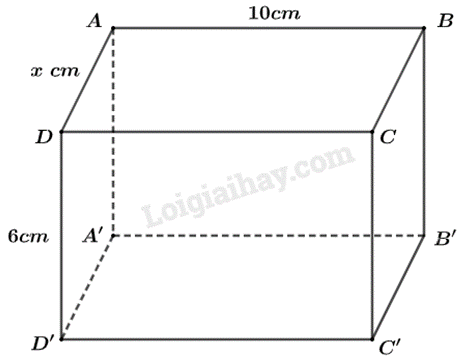
Đặt \(AD = x\left( {cm} \right)\).
Chu vi đáy của hình lăng trụ là: \(C = 2(AB + AD) = 2(10 + x)(cm)\)
Diện tích xung quanh của hình lăng trụ là:
\({S_{xq}} = C.h\)\( = 2.\left( {10 + x} \right).6\)\( = 12.\left( {10 + x} \right){\mkern 1mu} {\mkern 1mu} \left( {c{m^2}} \right)\)
Tổng diện tích hai đáy của hình lăng trụ là: \(2.10x = 20x{\mkern 1mu} {\mkern 1mu} (c{m^2})\)
Theo đề bài, ta có diện tích xung quanh bằng tổng diện tích hai đáy nên \(12.\left( {10 + x} \right) = 20x\)
Do đó \(120 + 12x = 20x\)
Suy ra \(x = 15{\mkern 1mu} \left( {cm} \right)\)
hay \(AD = 15\left( {cm} \right)\)
Vậy kích thước còn lại của đáy bằng 15 cm.
Bài 15: Một nhóm thợ xây có 100 khối bê tông có dạng như hình dưới đây.
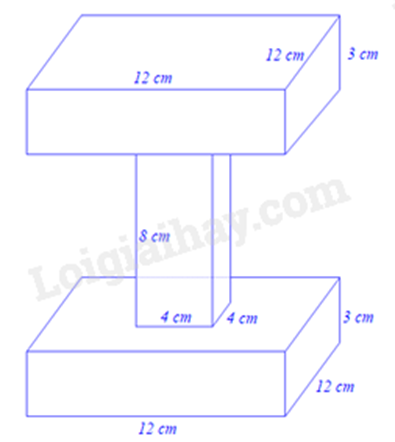
Người ta muốn sơn tất cả các mặt của từng khối bê tông. Hỏi số tiền sơn số bê tông đó là bao nhiêu đồng? Biết rằng số tiền để sơn 1 m2 bê tông là 100 000 đồng.
Phương pháp
- Ta chia khối bê tông thành ba hình khối có dạng hình hộp chữ nhật.
- Tính diện tích xung quanh của mỗi hình hộp chữ nhật.
- Tính diện tích 2 mặt đáy và 2 mặt giáp với hình hộp chữ nhật ở giữa. Với mặt giáp, ta cần trừ đi diện tích phần nối giữa hai hình hộp chữ nhật.
- Tính chi phí để sơn 1 khối bê tông, ta lấy diện tích 3 khối xung quanh cộng với diện tích 2 mặt đáy và 2 mặt giáp với hình hộp chữ nhật ở giữa đã trừ đi diện tích phần nối.
- Tính chi phí sơn 100 khối.
- Lưu ý khi tính để cùng một đơn vị đo.
Lời giải
Ta chia khối bê tông thành ba hình khối như hình vẽ dưới đây, trong đó hình (1) và hình (3) có diện tích tất cả các mặt bằng nhau.
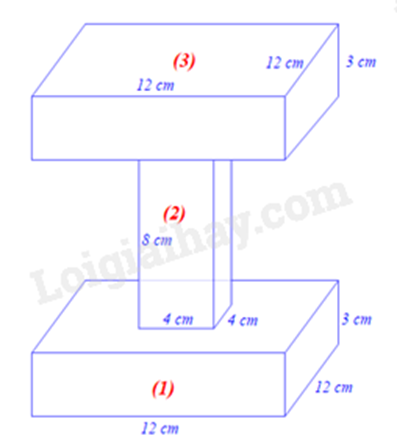
Diện tích xung quanh của hình hộp chữ nhật (1) là:
S1 = 2.(12 + 12).3 = 144 (cm2).
Diện tích một mặt đáy của hình hộp chữ nhật (1) là:
S2 = 12.12 = 144 (cm2).
Diện tích tiếp giáp giữa hình hộp chữ nhật (1) với hình hộp chữ nhật (2) chính là diện tích một mặt đáy của hình hộp chữ nhật (2) và bằng:
S3 = 4.4 = 16 (cm2).
Diện tích xung quanh của hình hộp chữ nhật (2) là:
S4 = 2.(4 + 4).8 = 128 (cm2).
Diện tích tiếp giáp giữa hình hộp chữ nhật (2) với hình hộp chữ nhật (3) bằng S3 = 16 (cm2).
Khi đó diện tích tất cả các mặt của khối bê tông là:
S = 2.[S1 + S2 + (S2 – S3)] + S4
= 2.[144 + 144 + (144 – 16)] + 128 = 960 (cm2) = 0,096 (m2).
Chi phí sơn một khối bê tông là: 0,096 . 100 000 = 9 600 (đồng)
Chi phí sơn 100 khối bê tông là: 9 600 . 100 = 960 000 (đồng).
Các bài khác cùng chuyên mục
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8












Danh sách bình luận