Dạng bài hai tam giác bằng nhau - Ôn hè Toán 7 lên 8
Tải vềDạng 2. Hai tam giác bằng nhau
Lý thuyết
* Khái niệm:
Hai tam giác bằng nhau là hai tam giác có cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta ký hiệu là \(\Delta ABC = \Delta A'B'C'\).
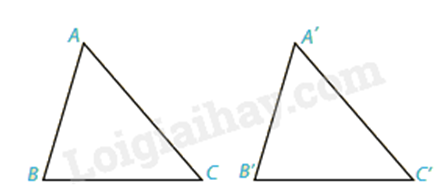
Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.
Chú ý:
- Nếu \(AB = A'B',BC = B'C',CA = C'A'\) và \(\widehat A = \widehat {A'},\widehat B = \widehat {B'},\widehat C = \widehat {C'}\) thì \(\Delta ABC = \Delta A'B'C'\).
- Nếu \(\Delta ABC = \Delta A'B'C'\) thì \(AB = A'B',BC = B'C',CA = C'A'\) và \(\widehat A = \widehat {A'},\widehat B = \widehat {B'},\widehat C = \widehat {C'}\).
* Các trường hợp bằng nhau của hai tam giác:
|
Trường hợp cạnh – cạnh – cạnh (c.c.c) Nếu 3 cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. |
Xét \(\Delta ABC\) và \(\Delta MNP\) có: AB = MN BC = NP AC = MP Vây \(\Delta ABC = \Delta MNP\left( {c.c.c} \right)\) |
|
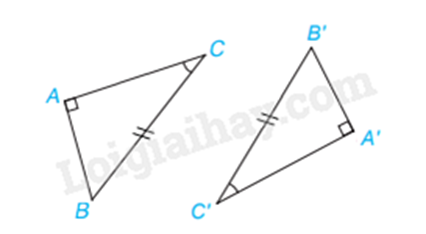
Trường hợp cạnh – góc – cạnh (c.g.c) Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. |
Xét \(\Delta ABC\) và \(\Delta MNP\) có: AB = MN \(\widehat {BAC} = \widehat {NMP}\) AC = MP Vây \(\Delta ABC = \Delta MNP\left( {c.g.c} \right)\) |
|
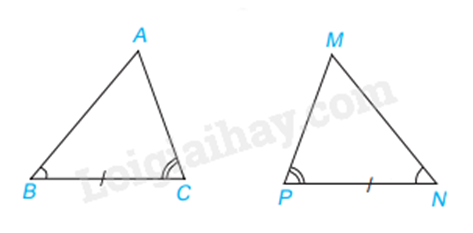
Trường hợp góc – cạnh – góc (g.c.g) Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 cạnh và 2 góc kề của tam giác kia thì hai tam giác đó bằng nhau. |
Xét \(\Delta ABC\) và \(\Delta MNP\) có: \(\widehat B = \widehat N\) BC = NP \(\widehat C = \widehat P\) Vây \(\Delta ABC = \Delta MNP\left( {g.c.g} \right)\) |
* Các trường hợp bằng nhau của hai tam giác vuông:
|
Trường hợp hai cạnh góc vuông Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Ta có thể kí hiệu là: (c.g.c) hoặc (hai cạnh góc vuông) |
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có: AB = A’B’ \(\widehat A = \widehat {A'}\left( { = 90^\circ } \right)\) AC = A’C’ Vậy \(\Delta ABC = \Delta A'B'C'\left( {c.g.c} \right)\) |
|
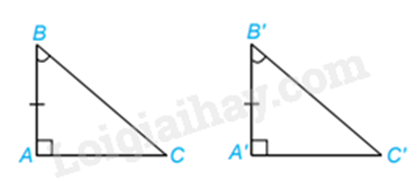
Trường hợp cạnh góc vuông – góc nhọn kề Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g.c.g) |
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có: \(\widehat A = \widehat {A'}\left( { = 90^\circ } \right)\) AB = A’B’ \(\widehat B = \widehat {B'}\) Vậy \(\Delta ABC = \Delta A'B'C'\left( {g.c.g} \right)\) |
|
Trường hợp cạnh huyền – góc nhọn Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (cạnh huyền – góc nhọn) |
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có: \(\widehat A = \widehat {A'}\left( { = 90^\circ } \right)\) BC = B’C’ \(\widehat C = \widehat {C'}\) Vậy \(\Delta ABC = \Delta A'B'C'\) (cạnh huyền – góc nhọn) |
Bài tập
Bài 1: Cho \(\Delta ABC = \Delta DEF.\) Cho \(\hat E = 46^\circ \). Khẳng định đúng là:
A. \(\hat A = 46^\circ \).
B. \(\hat B = 46^\circ \).
C. \(\hat F = 46^\circ \).
D. \(\hat F = 46^\circ \).
Bài 2: Cho hình vẽ sau. Tam giác bằng với tam giác DEA là:
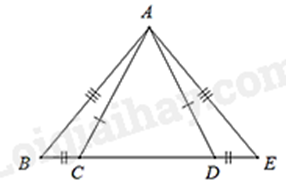
A. Tam giác ABC.
B. Tam giác CBA.
C. Tam giác DBA.
D. Tam giác BCA.
Bài 3: Cho tam giác BAC và tam giác KEF có \(BA = EK,\) \(\hat A = \hat K\), \(CA = KF.\) Phát biểu nào trong trong các phát biểu sau đây là đúng:
A. \(\Delta BAC = \Delta EKF\).
B. \(\Delta BAC = \Delta EFK\).
C. \(\Delta {\rm{A}}BC = \Delta FKE\).
D. \(\Delta BAC = \Delta KEF\).
Bài 4: Cho tam giác DEF và tam giác HKG có \(\hat D = \hat H\), \(\hat E = \hat K\), \(DE = HK.\) Biết \(\hat F = 80^\circ \). Số đo góc \(G\) là:
A. \(70^\circ \).
B. \(80^\circ \).
C. \(90^\circ \).
D. \(100^\circ \).
Bài 5: Cho tam giác ABC vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ BH và CK vuông góc với đường thẳng d. Khẳng định đúng là:
A. BH = CK.
B.\(\widehat {ABC} = \widehat {CAH}\).
C. \(\widehat {ABH} = \widehat {ACB}\).
D. AK = BH.
Bài 6: Cho hình vẽ bên, biết \(\widehat A = 100^\circ \), \(AB = DB\), \(AC = CD\).
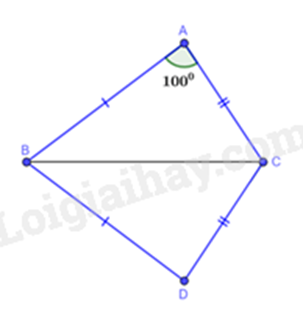
a) Tính số đo góc D.
b) Chứng tỏ rằng BC là tia phân giác của góc ABD.
Bài 7: Cho hai đoạn thẳng AB và DC cắt nhau tại trung điểm O của mỗi đoạn thẳng.
a) Chứng minh AC = BD và AC // BD; AD = BC và AD // BC.
b) Vẽ \(CH \bot AB\) tại H. Trên tia đối của tia OH lấy điểm I sao cho OI = OH. Chứng minh \(DI \bot AB\).
Bài 8: Cho góc nhọn \(xOy\) và tia phân giác Oz của góc đó. Qua điểm I thuộc tia Oz, kẻ đường thẳng vuông góc với Oz, đường thẳng này cắt tia \(Ox\), \(Oy\) lần lượt tại A và B.
a) Chứng minh rằng OA = OB.
b) Trên tia Oz lấy điểm C. Chứng minh \(\widehat {OAC} = \widehat {OBC}\).
Bài 9: Cho \(\widehat {xOy}\). Lấy hai điểm A và B thuộc tia \(Ox\) sao cho \(OA < OB\). Lấy hai điểm C và D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) \(\Delta EAB = \Delta ECD\).
c) \(OE\) là tia phân giác của \(\widehat {xOy}\).
Bài 10: Cho \(\Delta ABC\) có AB = AC. Vẽ BD và CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm của BD và CE.
a) Chứng minh \(\Delta AEI = \Delta ADI\).
b) Gọi M là trung điểm của BC. Chứng minh ba điểm A, I, M thẳng hàng.
--------Hết--------
Lời giải chi tiết:
Bài 1: Cho \(\Delta ABC = \Delta DEF.\) Cho \(\hat E = 46^\circ \). Khẳng định đúng là:
A. \(\hat A = 46^\circ \).
B. \(\hat B = 46^\circ \).
C. \(\hat F = 46^\circ \).
D. \(\hat F = 46^\circ \).
Phương pháp
Khi 2 tam giác bằng nhau thì các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Lời giải
Vì \(\Delta ABC = \Delta DEF\) nên \(\hat B = \hat E\) (2 góc tương ứng)
suy ra \(\hat B = 46^\circ \)
Đáp án: B
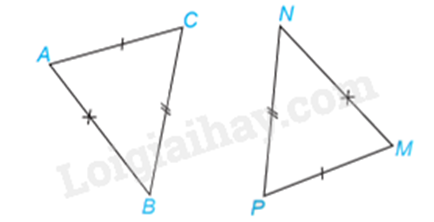
Bài 2: Cho hình vẽ sau. Tam giác bằng với tam giác DEA là:
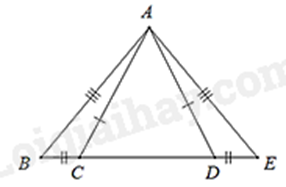
A. Tam giác ABC.
B. Tam giác CBA.
C. Tam giác DBA.
D. Tam giác BCA.
Phương pháp
Hai tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. (c.c.c)
Lời giải
Xét tam giác DEA và tam giác CBA, ta có:
DE = CB
EA = BA
DA = CA
suy ra \(\Delta DEA = \Delta CBA\) (c.c.c)
Đáp án: B
Bài 3: Cho tam giác BAC và tam giác KEF có \(BA = EK,\) \(\hat A = \hat K\), \(CA = KF.\) Phát biểu nào trong trong các phát biểu sau đây là đúng:
A. \(\Delta BAC = \Delta EKF\).
B. \(\Delta BAC = \Delta EFK\).
C. \(\Delta {\rm{A}}BC = \Delta FKE\).
D. \(\Delta BAC = \Delta KEF\).
Phương pháp
Sử dụng trường hợp bằng nhau thứ hai của tam giác.
Lời giải
Xét tam giác BAC và tam giác KEF có \(BA = EK,\) \(\hat A = \hat K\), \(CA = KF.\)
Suy ra \(\Delta BAC = \Delta EKF\) (c.g.c).
Đáp án: A
Bài 4: Cho tam giác DEF và tam giác HKG có \(\hat D = \hat H\), \(\hat E = \hat K\), \(DE = HK.\) Biết \(\hat F = 80^\circ \). Số đo góc \(G\) là:
A. \(70^\circ \).
B. \(80^\circ \).
C. \(90^\circ \).
D. \(100^\circ \).
Phương pháp
Áp dụng trường hợp bằng nhau thứ ba của tam giác để chứng minh hai tam giác bằng nhau, từ đó suy ra tính chất về góc của hai tam giác bằng nhau.
Lời giải
Xét tam giác DEF và tam giác HKG có \(\hat D = \hat H\), \(\hat E = \hat K\), \(DE = HK,\) do đó \(\Delta DEF = \Delta HKG\) (g.c.g).
Do đó \(\hat G = \hat F = 80^\circ \) (hai góc tương ứng).
Đáp án: B
Bài 5: Cho tam giác ABC vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ BH và CK vuông góc với đường thẳng d. Khẳng định đúng là:
A. BH = CK.
B.\(\widehat {ABC} = \widehat {CAH}\).
C. \(\widehat {ABH} = \widehat {ACB}\).
D. AK = BH.
Phương pháp
Chứng minh hai tam giác bằng nhau \(\Delta ABH = \Delta CAK\) suy ra các cạnh tương ứng bằng nhau
Lời giải
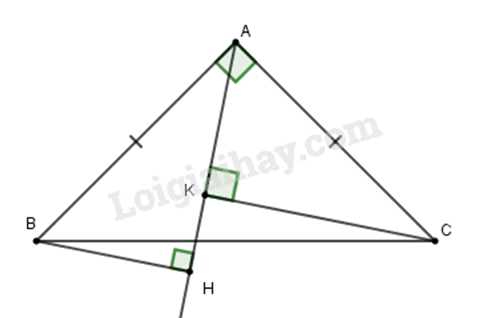
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất)
Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\) ) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \)
Nên \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\) )
\(\Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn) nên \(BH = AK.\) (2 cạnh tương ứng)
Đáp án: D
Bài 6: Cho hình vẽ bên, biết \(\widehat A = 100^\circ \), \(AB = DB\), \(AC = CD\).
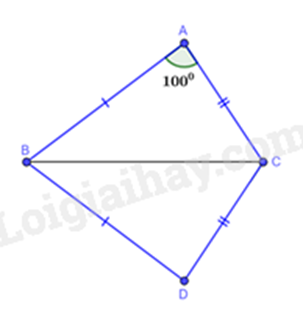
a) Tính số đo góc D.
b) Chứng tỏ rằng BC là tia phân giác của góc ABD.
Phương pháp
a) Chứng minh \(\Delta ABC = \Delta DBC\) suy ra hai góc tương ứng bằng nhau.
b) Chứng minh \(\widehat {ABC} = \widehat {DBC}\) nên BC là tia phân giác của góc ABD.
Lời giải
a) Xét \(\Delta ABC\) và \(\Delta DBC\) có:
AB = DB (gt)
AC = DC (gt)
BC là cạnh chung
nên \(\Delta ABC = \Delta DBC\) (c.c.c)
Suy ra \(\widehat D = \widehat A = 100^\circ \).
b) Vì \(\Delta ABC = \Delta DBC\) (cmt) nên \(\widehat {ABC} = \widehat {DBC}\) hay BC là tia phân giác của góc ABD.
Bài 7: Cho hai đoạn thẳng AB và DC cắt nhau tại trung điểm O của mỗi đoạn thẳng.
a) Chứng minh AC = BD và AC // BD; AD = BC và AD // BC.
b) Vẽ \(CH \bot AB\) tại H. Trên tia đối của tia OH lấy điểm I sao cho OI = OH. Chứng minh \(DI \bot AB\).
Phương pháp
a) Chứng minh \(\Delta AOC = \Delta BOD\) (c.g.c)
Suy ra AC = BD và \(\widehat {{A_1}} = \widehat {{B_1}}\)
Hai góc này ở vị trí so le trong nên AC // BD.
Chứng minh tương tự \(\Delta AOD = \Delta BOC\) để có AD = BC và AD // BC.
b) Chứng minh \(\Delta COH = \Delta DOI\) (c.g.c)
Suy ra \(\widehat {DIO} = 90^\circ \) nên \(DI \bot AB\).
Lời giải
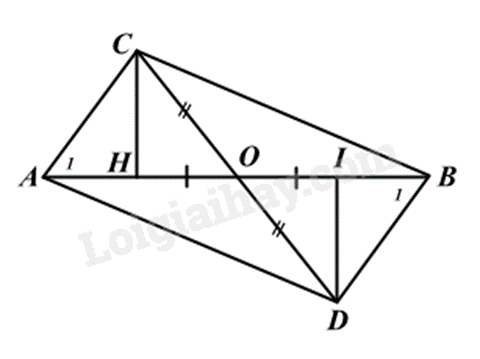
Xét \(\Delta AOC\) và \(\Delta BOD\) có:
\(\widehat {AOC} = \widehat {BOC}\) (hai góc đối đỉnh)
\(OA = OB\) (gt)
\(OC = OD\) (gt)
Do đó \(\Delta AOC = \Delta BOD\) (c.g.c)
Suy ra \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên AC // BD.
Vì \(\Delta AOC = \Delta BOD\) nên AC = BD (hai cạnh tương ứng)
Chứng minh tương tự với \(\Delta AOD\) và \(\Delta BOC\) để có AD = BC và AD // BC.
b) Xét \(\Delta COH\) và \(\Delta DOI\) có:
\(\widehat {COH} = \widehat {DOI}\) (hai góc đối đỉnh)
OH = OI (gt)
OC = OB (gt)
Do đó \(\Delta COH = \Delta DOI\) (c.g.c)
Suy ra \(\widehat {DIO} = \widehat {CHO} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DI \bot AB\).
Bài 8: Cho góc nhọn \(xOy\) và tia phân giác Oz của góc đó. Qua điểm I thuộc tia Oz, kẻ đường thẳng vuông góc với Oz, đường thẳng này cắt tia \(Ox\), \(Oy\) lần lượt tại A và B.
a) Chứng minh rằng OA = OB.
b) Trên tia Oz lấy điểm C. Chứng minh \(\widehat {OAC} = \widehat {OBC}\).
Phương pháp
a) Chứng minh \(\Delta OAI = \Delta OBI\) (g.c.g)
Suy ra \(OA = OB\) (hai cạnh tương ứng)
b) Chứng minh \(\Delta OAC = \Delta OBC\) (c.g.c)
Suy ra \(\widehat {OAC} = \widehat {OBC}\) (hai góc tương ứng).
Lời giải
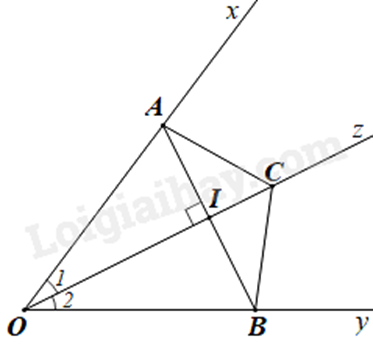
a) Vì Oz là tia phân giác của góc \(xOy\) nên ta có: \(\widehat {{O_1}} = \widehat {{O_2}}\).
Xét \(\Delta OAI\) và \(\Delta OBI\) có:
\(\widehat {{O_1}} = \widehat {{O_2}}\) (gt)
OI là cạnh chung
\(\widehat {OIA} = \widehat {OIB}\left( { = 90^\circ } \right)\) (gt)
Do đó \(\Delta OAI = \Delta OBI\) (g.c.g)
Suy ra \(OA = OB\) (hai cạnh tương ứng)
b) Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(OC\) là cạnh chung
\(\widehat {{O_1}} = \widehat {{O_2}}\)
\(OA = OB\) (cmt)
Do đó \(\Delta OAC = \Delta OBC\) (c.g.c)
Suy ra \(\widehat {OAC} = \widehat {OBC}\) (hai góc tương ứng).
Bài 9: Cho \(\widehat {xOy}\). Lấy hai điểm A và B thuộc tia \(Ox\) sao cho \(OA < OB\). Lấy hai điểm C và D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) \(\Delta EAB = \Delta ECD\).
c) \(OE\) là tia phân giác của \(\widehat {xOy}\).
Phương pháp
a) Chứng minh \(\Delta AOD = \Delta COB\) (c.g.c)
Suy ra \(AD = BC\) (cạnh tương ứng)
b) Chứng minh \(CD = AB\)
Chứng minh \(\widehat {DCE} = \widehat {BAE}\)
Suy ra \(\Delta EAB = \Delta ECD\) (g.c.g)
c) Chứng minh \(\Delta OED = \Delta OEB\) (c.c.c)
suy ra \(\widehat {DOE} = \widehat {BOE}\) (góc tương ứng) nên OE là tia phân giác của góc xOy.
Lời giải
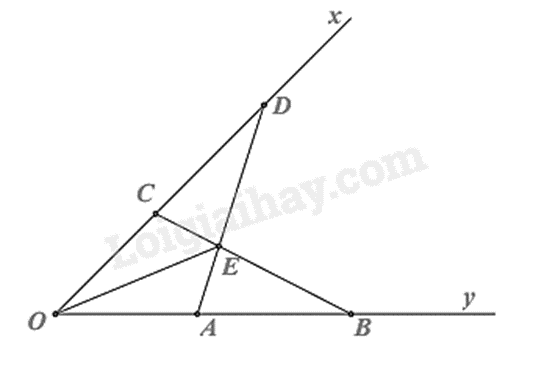
a) Xét \(\Delta AOD\) và \(\Delta COB\) có
\(OA = OC\) (gt)
\(\widehat O\) chung
\(OD = OB\) (gt)
Do đó \(\Delta AOD = \Delta COB\) (c.g.c)
Suy ra \(AD = BC\) (cạnh tương ứng)
b) Ta có: \(OD = OB\) (gt)
\(OC = OA\) (gt)
suy ra \(OD - OC = OB - OA\) hay \(CD = AB\)
\(\widehat {DCE} + \widehat {OCB} = 180^\circ \) (kề bù), tương tự \(\widehat {BAE} + \widehat {OAD} = 180^\circ \)
Mà \(\widehat {OCB} = \widehat {OAD}\) (do \(\Delta AOD = \Delta COB\)) suy ra \(\widehat {DCE} = \widehat {BAE}\)
Xét \(\Delta EAB\) và \(\Delta ECD\) có:
\(\widehat B = \widehat D\) (do \(\Delta AOD = \Delta COB\))
\(AB = CD\) (cmt)
\(\widehat {DCE} = \widehat {BAE}\) (cmt)
Do đó: \(\Delta EAB = \Delta ECD\) (g.c.g)
c) Xét \(\Delta OED\) và \(\Delta OEB\) có
OE cạnh chung
\(ED = EB\) (do \(\Delta EAB = \Delta ECD\))
\(OD = OB\) (gt)
Do đó \(\Delta OED = \Delta OEB\) (c.c.c)
suy ra \(\widehat {DOE} = \widehat {BOE}\) (góc tương ứng)
Do đó OE là tia phân giác của góc xOy.
Bài 10: Cho \(\Delta ABC\) có AB = AC. Vẽ BD và CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm của BD và CE.
a) Chứng minh \(\Delta AEI = \Delta ADI\).
b) Gọi M là trung điểm của BC. Chứng minh ba điểm A, I, M thẳng hàng.
Phương pháp
a) Chứng minh \(\Delta AEC = \Delta ADB\) (ch – gn)
suy ra \(AE = AD\) (hai cạnh tương ứng)
Từ đó chứng minh \(\Delta AEI = \Delta ADI\) (ch – cgv)
b) Chứng minh \(\Delta AMB = \Delta AMC\) (c.c.c) nên AM là tia phân giác của \(\widehat {BAC}\).
Từ \(\Delta AEI = \Delta ADI\) suy ra AI là tia phân giác của \(\widehat {BAC}\).
Suy ra A, M, I thẳng hàng.
Lời giải
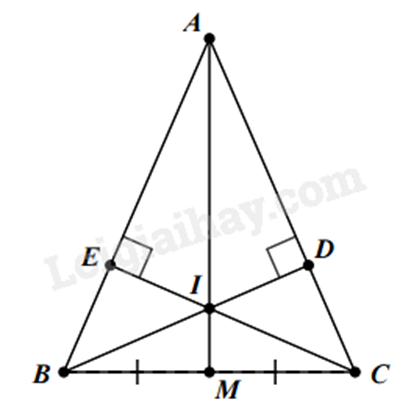
a) Xét \(\Delta AEC\) và \(\Delta ADB\) có:
\(\widehat A\) chung
AC = AB (gt)
\(\widehat {AEC} = \widehat {ADB}\left( { = 90^\circ } \right)\) (gt)
Do đó \(\Delta AEC = \Delta ADB\) (ch – gn)
suy ra \(AE = AD\) (hai cạnh tương ứng)
Xét \(\Delta AEI\) và \(\Delta ADI\) có:
\(\widehat {AEI} = \widehat {ADI}\left( { = 90^\circ } \right)\) (gt)
\(AI\) là cạnh chung
\(AE = AD\) (cmt)
Suy ra \(\Delta AEI = \Delta ADI\) (ch – cgv)
b) Xét \(\Delta AMB\) và \(\Delta AMC\) có:
\(AM\) là cạnh chung
\(AB = AC\) (gt)
\(MB = MC\) (M là trung điểm của BC)
Do đó \(\Delta AMB = \Delta AMC\) (c.c.c)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) (hai góc tương ứng), suy ra AM là tia phân giác của \(\widehat {BAC}\).
Lại có \(\Delta AEI = \Delta ADI\) (cmt) nên \(\widehat {EAI} = \widehat {DAI}\), suy ra AI là tia phân giác của \(\widehat {BAC}\).
Hai điểm M và I cùng thuộc tia phân giác của góc BAC nên A, M, I thẳng hàng.
- Dạng bài tam giác cân, vuông, vuông cân, đều - Ôn hè Toán 7 lên 8
- Dạng bài đường vuông góc và đường xiên - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài góc và cạnh của một tam giác - Ôn hè Toán 7 lên 8
>> Xem thêm
Các bài khác cùng chuyên mục
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8













Danh sách bình luận