Dạng bài so sánh số hữu tỉ - Ôn hè Toán 7 lên 8

Lý thuyết

* So sánh các số hữu tỉ:

Viết \(x,y\) dưới dạng hai số cùng mẫu số dương \(x = \frac{a}{m},y = \frac{b}{m}\left( {m > 0} \right)\).

+ Nếu \(a < b\) thì \(x < y\).

+ Nếu \(a > b\) thì \(x > y\).

+ Nếu \(a = b\) thì \(x = y\).

Lưu ý:

- Nếu \(b > 0,d > 0\) thì \(\frac{a}{b} > \frac{c}{d}\) khi và chỉ khi \(ad > bc\).

- Nếu \(\frac{a}{b} - 1 > \frac{c}{d} - 1\) thì \(\frac{a}{b} > \frac{c}{d}\).

- Nếu \(\frac{a}{b} + 1 > \frac{c}{d} + 1\) thì \(\frac{a}{b} > \frac{c}{d}\).

* So sánh hai luỹ thừa:

Với \(a,b \in \mathbb{Q};m,n \in \mathbb{Z}\). Ta có:

+ Tính chất 1: Nếu \(a > b > 0\) thì \({a^n} > {b^n}\).

+ Tính chất 2: Nếu \(a > b\) thì \({a^{2n + 1}} > {b^{2n + 1}}\).

+ Tính chất 3: Nếu \(a > 1,m > n > 0\) thì \({a^m} > {a^n}\).

+ Tính chất 4: Nếu \(0 < a < 1,m > n > 0\) thì \({a^m} < {a^n}\).

Bài tập

Bài 1: So sánh hai phân số: \(x = \frac{{11}}{{ - 24}}\) và \(y = \frac{{ - 7}}{{18}}\).

A. \(x < y\).

B. \(x = y\).

C. \(x > y\).

D. \(x \ge y\).

Bài 2: So sánh hai số \(a = \frac{4}{{15}}\) và \(b =  - \frac{{ - 8}}{{21}}\).

A. \(a > b\).

B. \(a < b\).

C. \(a = b\).

D. \(a \le b\).

Bài 3: So sánh \(x = \frac{{2022}}{{2021}}\) và \(y = \frac{{15}}{{16}}\)

A. \(x \ge y\).

B. \(y \ge x\).

C. \(x > y\).

D. \(x < y\).

Bài 4: So sánh \(x = \frac{{2020}}{{2021}}\) và \(y = \frac{{1000}}{{999}}\).

A. \(y = x\).

B. \(y < x\).

C. \(y > x\).

D. \(x \ge y\).

Bài 5: Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây.

Hỏi bạn nào chạy nhanh nhất?

A. An.

B. Bình.

C. Chi.

D. Duy.

Bài 6: Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:

A. \(\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}\).

B. \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\).

C. \(\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}\).

D. \(\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}\).

Bài 7: So sánh các số hữu tỉ sau:

a) \(\frac{{ - 1}}{4}\) và \(\frac{1}{{100}}\)

b) \(\frac{1}{{ - 2}}\) và \(\frac{{ - 1}}{3}\)

c) \(\frac{{ - 2}}{3}\) và \(\frac{{ - 3}}{{ - 5}}\)

d) \( - 2,5\) và \(\frac{5}{{ - 2}}\)

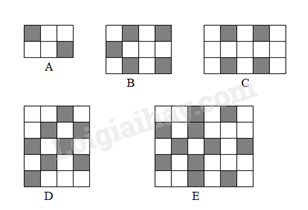
Bài 8: Lưới nào sẫm nhất?

a) Đối với mỗi lưới ô vuông ở hình trên, hãy lập một phân số có tử là số ô sẫm, mẫu là tổng số ô sẫm và trắng.

b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô sẫm so với tổng số ô là lớn nhất).

Bài 9: So sánh các phân số sau:

a) \(\frac{{1234}}{{1235}}\) và \(\frac{{4319}}{{4320}}\)

b) \(\frac{{22}}{{ - 67}}\) và \(\frac{{51}}{{ - 152}}\)

 c) \(\frac{{ - 18}}{{91}}\) và \(\frac{{ - 23}}{{114}}\)

Bài 10: Trong dịp hè, bạn An muốn mua một số vở để chuẩn bị cho năm học mới. Cửa hàng có 2 loại vở: 6 quyển vở Hồng Hà có giá 65 nghìn đồng và 9 quyển vở Campus có giá 103 nghìn đồng. Hỏi để tiết kiệm tiền bạn An nên mua loại vở nào?

--------Hết--------

Lời giải chi tiết:

Bài 1: So sánh hai phân số: \(x = \frac{{11}}{{ - 24}}\) và \(y = \frac{{ - 7}}{{18}}\).

A. \(x < y\).

B. \(x = y\).

C. \(x > y\).

D. \(x \ge y\).

Phương pháp

Quy đồng đưa hai phân số về cùng mẫu dương rồi so sánh hai tử số với nhau.

Lời giải

Ta có: \(x = \frac{{11}}{{ - 24}} = \frac{{11.( - 3)}}{{ - 24.( - 3)}} = \frac{{ - 33}}{{72}}\)

           \(y = \frac{{ - 7}}{{18}}\frac{{ - 7.4}}{{18.4}} = \frac{{ - 28}}{{72}}\)

Mà \( - 33 <  - 28\) nên \(\frac{{ - 33}}{{72}} < \frac{{ - 28}}{{72}}\).

Vậy \(x < y\).

Đáp án: A

Bài 2: So sánh hai số \(a = \frac{4}{{15}}\) và \(b =  - \frac{{ - 8}}{{21}}\).

A. \(a > b\).

B. \(a < b\).

C. \(a = b\).

D. \(a \le b\).

Phương pháp

Để so sánh hai số đã cho:

+ Viết hai số dưới dạng hai phân số có cùng một mẫu dương

+ So sánh các tử số với nhau, phân số nào có tử lớn hơn thì lớn hơn.

Lời giải

Ta có: \(a = \frac{4}{{15}} = \frac{{4.7}}{{15.7}} = \frac{{28}}{{105}}\);

\(b =  - \frac{{ - 8}}{{21}} = \frac{8}{{21}} = \frac{{8.5}}{{21.5}} = \frac{{40}}{{105}}\) 

Vì \(28 < 40\) nên \(\frac{{28}}{{105}} < \frac{{40}}{{105}}\) hay \(a < b\).

Đáp án: B

Bài 3: So sánh \(x = \frac{{2022}}{{2021}}\) và \(y = \frac{{15}}{{16}}\)

A. \(x \ge y\).

B. \(y \ge x\).

C. \(x > y\).

D. \(x < y\).

Phương pháp

So sánh với số \(1\).

Lời giải

Ta có \(x = \frac{{2022}}{{2021}} > \frac{{2021}}{{2021}} = 1\) hay \(x > 1\)

Và \(y = \frac{{15}}{{16}} < \frac{{16}}{{16}} = 1\) hay \(y < 1\)

Từ đó suy ra \(x > 1 > y\) hay \(x > y\) .

Đáp án: C

Bài 4: So sánh \(x = \frac{{2020}}{{2021}}\) và \(y = \frac{{1000}}{{999}}\).

A. \(y = x\).

B. \(y < x\).

C. \(y > x\).

D. \(x \ge y\).

Phương pháp

So sánh hai số với số \(1\): Nếu \(\frac{a}{b} > 1\) và \(1 > \frac{c}{d}\) thì \(\frac{a}{b} > \frac{c}{d}\).

Lời giải

Ta có: \(x = \frac{{2020}}{{2021}} < \frac{{2021}}{{2021}} = 1\) hay \(x < 1\);

\(y = \frac{{1000}}{{999}} > \frac{{999}}{{999}} = 1\) hay \(y > 1\)

Từ đó suy ra \(y > 1 > x\) hay \(y > x\).

Đáp án: C

Bài 5: Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây.

Hỏi bạn nào chạy nhanh nhất?

A. An.

B. Bình.

C. Chi.

D. Duy.

Phương pháp

So sánh thành tích của các bạn: So sánh các số hữu tỉ

Bạn nào có thời gian chạy nhỏ nhất thì bạn đó chạy nhanh nhất.

Lời giải

Ta có: \(\frac{1}{3}\)phút = \(\frac{1}{3}\) . 60 = 20 giây

\(\frac{{108}}{5}\) giây = 21,6 giây

\(20\frac{3}{8}\) giây = 20,375 giây

Vì 20 < 20,375 < 21,54 < 21,6 nên Bình chạy nhanh nhất

Đáp án: B

Bài 6: Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:

A. \(\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}\).

B. \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\).

C. \(\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}\).

D. \(\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}\).

Phương pháp

+ Dùng tính chất: Nếu a < b thì –a > - b

+ Các phân số có cùng mẫu số dương: phân số nào có tử số lớn hơn thì phân số đó lớn hơn

+ Các phân số dương có cùng tử số: phân số nào có mẫu số lớn hơn thì nhỏ hơn

Lời giải

+ So sánh \(\frac{5}{{ - 20}}\) và \(\frac{{ - 5}}{{17}}\):

Vì 20 > 17 nên \(\frac{5}{{20}} < \frac{5}{{17}}\), do đó \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}}\)

+ So sánh \(\frac{{ - 5}}{{17}}\) và \(\frac{1}{{ - 3}}\):

Vì \(\frac{5}{{17}} < \frac{5}{{15}}\) nên \(\frac{{ - 5}}{{17}} > \frac{{ - 5}}{{15}} = \frac{1}{{ - 3}}\)

+ So sánh \(\frac{1}{{ - 3}}\) và \(\frac{{ - 7}}{{20}}\):

Vì \(\frac{7}{{20}} > \frac{7}{{21}}\) nên \(\frac{{ - 7}}{{20}} < \frac{{ - 7}}{{21}} = \frac{1}{{ - 3}}\)

Do đó, \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}} > \frac{1}{{ - 3}} > \frac{{ - 7}}{{20}}\)

Đáp án: A

Bài 7: So sánh các số hữu tỉ sau:

a) \(\frac{{ - 1}}{4}\) và \(\frac{1}{{100}}\)

b) \(\frac{1}{{ - 2}}\) và \(\frac{{ - 1}}{3}\)

c) \(\frac{{ - 2}}{3}\) và \(\frac{{ - 3}}{{ - 5}}\)

d) \( - 2,5\) và \(\frac{5}{{ - 2}}\)

Phương pháp

a) So sánh hai số hữu tỉ với 0.

b) So sánh \(\frac{1}{2}\) và \(\frac{1}{3}\) suy ra so sánh được \(\frac{1}{{ - 2}}\) và \(\frac{{ - 1}}{3}\) (đổi dấu).

c) So sánh hai số hữu tỉ với 0.

d) Đưa về cùng dạng phân số để so sánh.

Lời giải

a) \(\frac{{ - 1}}{4}\) và \(\frac{1}{{100}}\)   

Vì \(\frac{{ - 1}}{4} < 0\,;\,\frac{1}{{100}} > 0\) nên \(\frac{{ - 1}}{4} < \frac{1}{{100}}\)

b) \(\frac{1}{{ - 2}}\) và \(\frac{{ - 1}}{3}\)   

Vì 2 < 3 nên \(\frac{1}{2} > \frac{1}{3}\)

Do đó \(\frac{1}{{ - 2}} < \frac{{ - 1}}{3}\)

c) \(\frac{{ - 2}}{3}\) và \(\frac{{ - 3}}{{ - 5}}\)

Ta có: \(\frac{{ - 3}}{{ - 5}} = \frac{3}{5} > \frac{{ - 2}}{3}\) (do \(\frac{3}{5} > 0;0 > \frac{{ - 2}}{3}\))

Vậy \(\frac{{ - 2}}{3} < \frac{{ - 3}}{{ - 5}}\)

d) \( - 2,5\) và \(\frac{5}{{ - 2}}\)

Ta có: \( - 2,5 = \frac{{ - 5}}{2} = \frac{5}{{ - 2}}\)

Vậy \( - 2,5 = \frac{5}{{ - 2}}\)

Bài 8: Lưới nào sẫm nhất?

a) Đối với mỗi lưới ô vuông ở hình trên, hãy lập một phân số có tử là số ô sẫm, mẫu là tổng số ô sẫm và trắng.

b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô sẫm so với tổng số ô là lớn nhất).

Phương pháp

a) Quan sát hình vẽ, đếm số ô sẫm màu, tổng số ô của từng hình để lập phân số tương ứng.

b) Đưa các phân số về cùng mẫu dương.

So sánh tử số, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

Lời giải

a) A. \(\frac{2}{6}\); B. \(\frac{5}{{12}}\); C. \(\frac{4}{{15}}\); D. \(\frac{8}{{20}}\); E. \(\frac{{11}}{{30}}\).

b) Ta có: \(\frac{2}{6} = \frac{{20}}{{60}};{\rm{ }}\frac{5}{{12}} = \frac{{25}}{{60}};{\rm{ }}\frac{4}{{15}} = \frac{{16}}{{60}};\) \(\frac{8}{{20}} = \frac{{24}}{{60}};{\rm{ }}\frac{{11}}{{30}} = \frac{{22}}{{60}}\)

Mà 16 < 20 < 22 < 24 < 25 nên \(\frac{{16}}{{60}} < \frac{{20}}{{60}} < \frac{{22}}{{60}} < \frac{{24}}{{60}} < \frac{{25}}{{60}}\)

hay \(\frac{4}{{15}} < \frac{2}{6} < \frac{{11}}{{30}} < \frac{8}{{20}} < \frac{5}{{12}}\).

Vậy lưới \(B\) sẫm nhất.

Bài 9: So sánh các phân số sau:

a) \(\frac{{1234}}{{1235}}\) và \(\frac{{4319}}{{4320}}\)

b) \(\frac{{22}}{{ - 67}}\) và \(\frac{{51}}{{ - 152}}\)

 c) \(\frac{{ - 18}}{{91}}\) và \(\frac{{ - 23}}{{114}}\)

Phương pháp

a) Sử dụng: Nếu \(\frac{a}{b} - 1 > \frac{c}{d} - 1\) thì \(\frac{a}{b} > \frac{c}{d}\).

b) So sánh qua phân số trung gian \( - \frac{1}{3}\).

c) So sánh qua phân số trung gian \( - \frac{1}{5}\).

Lời giải

a) \(\frac{{1234}}{{1235}}\) và \(\frac{{4319}}{{4320}}\)

Ta có: \(\frac{{1234}}{{1235}} - 1 = \frac{{ - 1}}{{1235}};\frac{{4319}}{{4320}} - 1 = \frac{{ - 1}}{{4320}}\)

Vì \(1235 < 4320\) nên \(\frac{{ - 1}}{{1235}} < \frac{{ - 1}}{{4320}}\), suy ra \(\frac{{1234}}{{1235}} - 1 < \frac{{4319}}{{4320}} - 1\).

Do đó \(\frac{{1234}}{{1235}} < \frac{{4319}}{{4320}}\).

b) \(\frac{{22}}{{ - 67}}\) và \(\frac{{51}}{{ - 152}}\)

Ta có:

\(\begin{array}{l}\frac{{22}}{{ - 67}} = \frac{{ - 22}}{{67}} > \frac{{ - 22}}{{66}} = \frac{{ - 1}}{3};\\\frac{{ - 1}}{3} = \frac{{ - 51}}{{153}} > \frac{{ - 51}}{{152}} = \frac{{51}}{{ - 152}}\end{array}\)

Do đó \(\frac{{22}}{{ - 67}} > \frac{{51}}{{ - 152}}\).

c) \(\frac{{ - 18}}{{91}}\) và \(\frac{{ - 23}}{{114}}\)

Ta có:

\(\begin{array}{l}\frac{{ - 18}}{{91}} > \frac{{ - 18}}{{90}} = \frac{{ - 1}}{5};\\\frac{{ - 1}}{5} = \frac{{ - 23}}{{115}} > \frac{{ - 23}}{{114}}\end{array}\)

Do đó  \(\frac{{ - 18}}{{91}} > \frac{{ - 23}}{{114}}\).

Bài 10: Trong dịp hè, bạn An muốn mua một số vở để chuẩn bị cho năm học mới. Cửa hàng có 2 loại vở: 6 quyển vở Hồng Hà có giá 65 nghìn đồng và 9 quyển vở Campus có giá 103 nghìn đồng. Hỏi để tiết kiệm tiền bạn An nên mua loại vở nào?

Phương pháp

Tính giá tiền mỗi quyển vở Hồng Hà, vở Campus.

So sánh hai phân số bằng cách quy đồng mẫu.

Lời giải

Giá tiền mỗi quyển vở Hồng Hà là: \(\frac{{65}}{6}\) (nghìn đồng).

Giá tiền mỗi quyển vở Campus là: \(\frac{{103}}{9}\) (nghìn đồng).

Quy đồng mẫu số hai phân số ta có: \(\frac{{65}}{6} = \frac{{195}}{{18}};{\rm{ }}\frac{{103}}{9} = \frac{{206}}{{18}}\)

Vì \(\frac{{195}}{{18}} < \frac{{206}}{{18}}\) nên \(\frac{{65}}{6} < \frac{{103}}{9}\).

Vậy để tiết kiệm tiền bạn An nên mua vở Hồng Hà.