Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
Tải vềDạng 2. Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác
Lý thuyết
|
|
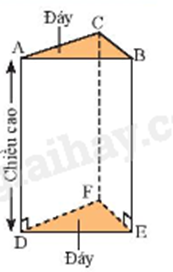
Hình lăng trụ đứng tam giác
|
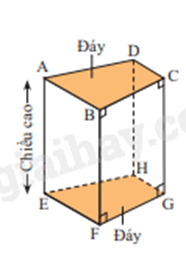
Hình lăng trụ đứng tứ giác
|
|
Đặc điểm |
- 6 đỉnh - 3 mặt bên là hình chữ nhật - 3 cạnh bên bằng nhau và song song với nhau (chiều cao của lăng trụ) - 2 mặt đáy là hình tam giác |
- 8 đỉnh - 4 mặt bên là hình chữ nhật - 4 cạnh bên bằng nhau và song song với nhau (chiều cao của lăng trụ) - 2 mặt đáy là hình tứ giác |
|
Diện tích xung quanh |
Sxq = chu vi đáy . chiều cao |
|
|
Diện tích toàn phần |
Stp = Sxq + S2 đáy |
|
|
Thể tích |
V = diện tích đáy . chiều cao |
|
Lưu ý:
- Hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác.
- Một số công thức tính chu vi và diện tích hình học quen thuộc:
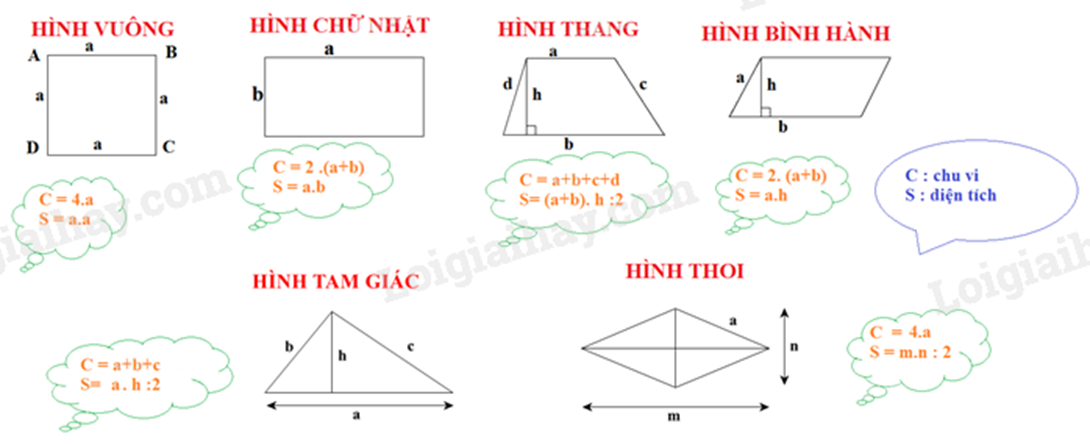
Bài tập
Bài 1: Cho các hình vẽ sau. Hình nào có dạng hình lăng trụ đứng?

A. Hình 1 và Hình 2.
B. Hình 2 và Hình 3.
C. Hình 3.
D. Tất cả các hình trên.
Bài 2: Hình lăng trụ đứng tam giác có tất cả bao nhiêu cạnh?
A. 9.
B. 6.
C. 12.
D. 8.
Bài 3: Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
B. Các mặt bên của hình lăng trụ đứng là các hình thang cân.
C. Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật.
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác.
Bài 4: Hình lăng trụ đứng tứ giác có đáy là hình thang cân có bao nhiêu mặt bên?
A. \(3\).
B. \(4\).
C. \(5\).
D. \(6\).
Bài 5: Tính thể tích của hình lăng trụ đứng có chiều cao 20cm, đáy là một tam giác vuông có các cạnh góc vuông lần lượt là 8cm và 10cm.
A. \(800c{m^3}\).
B. \(400c{m^3}\).
C. \(600c{m^3}\).
D. \(500c{m^3}\).
Bài 6: Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước \(3cm,{\mkern 1mu} {\mkern 1mu} 8cm\). Chiều cao của hình lăng trụ đứng là 2cm. Diện tích xung quanh của hình lăng trụ đứng là
A. \(44c{m^2}\).
B. \(24c{m^2}\).
C. \(48c{m^2}\).
D. \(22c{m^2}\).
Bài 7: Cho hình lăng trụ đứng có diện tích xung quanh bằng 336 cm2, chiều cao 14 cm. Khi đó, chu vi đáy của hình lăng trụ đứng là:
A. 12cm.
B. 24cm.
C. 36cm.
D. 48cm.
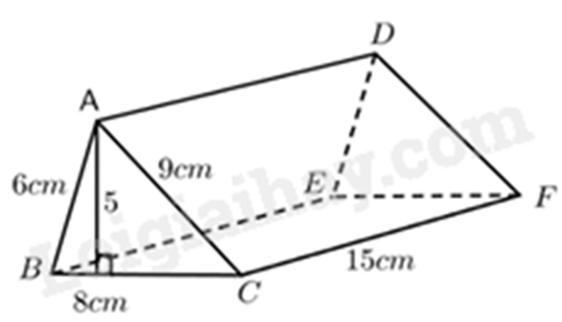
Bài 8: Tính diện tích xung quanh và thể tích của hình lăng trụ ABC.DEF?
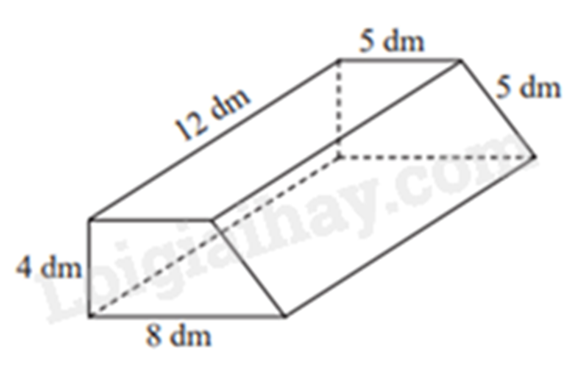
Bài 9: Một cái bục hình lăng trụ đứng tứ giác có kích thước như hình vẽ bên.
a) Tính diện tích xung quanh hình lăng trụ.
b) Người ta muốn sơn tất cả các mặt của cái bục trừ mặt nằm dưới đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
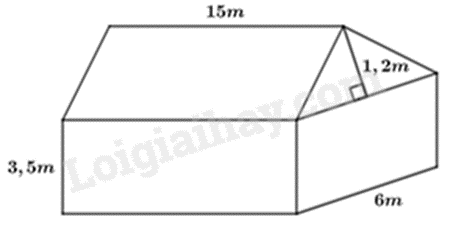
Bài 10: Tính thể tích phần không gian của một ngôi nhà dạng một lăng trụ đứng theo các kích thước đã cho trong hình.
Bài 11: Người ta đào một đoạn mương dài 20 m, sâu 1,5 m. Bề mặt của mương rộng 1,8 m và đáy mương rộng 1,2 m. Tính thể tích khối đất phải đào.
Bài 12: Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng 6 m. Đường cao của đáy (là chiều rộng của nhà kho) bằng 5 m. Các cạnh đáy của hình thang vuông dài 3 m và 4 m. Tính thể tích của nhà kho.
Bài 13: Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
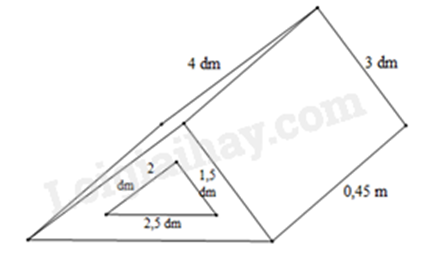
a) Tính thể tích của khối gỗ.
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
--------Hết--------
Lời giải chi tiết:
Bài 1: Cho các hình vẽ sau. Hình nào có dạng hình lăng trụ đứng?

A. Hình 1 và Hình 2.
B. Hình 2 và Hình 3.
C. Hình 3.
D. Tất cả các hình trên.
Phương pháp
Dựa vào kiến thức về hình lăng trụ đứng.
Hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác.
Lời giải
Cả 3 hình đều là hình lăng trụ đứng, trong đó Hình 1 và Hình 2 là hình lăng trụ đứng tứ giác (hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác); Hình 3 là hình lăng trụ đứng tam giác.
Đáp án: D
Bài 2: Hình lăng trụ đứng tam giác có tất cả bao nhiêu cạnh?
A. 9.
B. 6.
C. 12.
D. 8.
Phương pháp
Đặc điểm hình lăng trụ đứng tam giác.
Lời giải
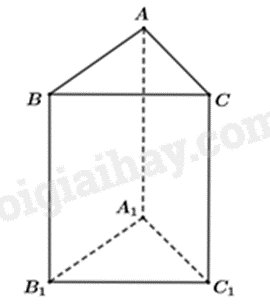
Các cạnh của hình lăng trụ đứng tam giác là: \(AB,{\mkern 1mu} {\mkern 1mu} AC,{\mkern 1mu} {\mkern 1mu} BC,{\mkern 1mu} {\mkern 1mu} {A_1}{B_1},\)\({A_1}{C_1},{\mkern 1mu} {\mkern 1mu} {B_1}{C_1},{\mkern 1mu} {\mkern 1mu} A{A_1},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B{B_1},{\mkern 1mu} C{C_1}\)
Vậy hình lăng trụ đứng tam giác có tất cả \(9\) cạnh.
Đáp án: A
Bài 3: Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
B. Các mặt bên của hình lăng trụ đứng là các hình thang cân.
C. Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật.
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác.
Phương pháp
Đặc điểm hình lăng trụ đứng tam giác.
Lời giải
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Đáp án: A
Bài 4: Hình lăng trụ đứng tứ giác có đáy là hình thang cân có bao nhiêu mặt bên?
A. \(3\).
B. \(4\).
C. \(5\).
D. \(6\).
Phương pháp
Đặc điểm lăng trụ đứng tứ giác.
Lời giải
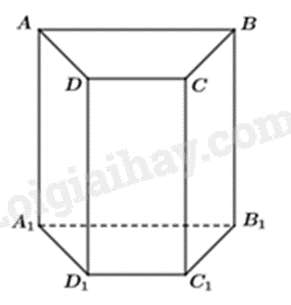
Hình lăng trụ đứng \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có đáy \({A_1}{B_1}{C_1}{D_1}\) là hình thang cân, có các mặt bên là: \(AD{D_1}{A_1};{\mkern 1mu} {\mkern 1mu} AB{B_1}{A_1};{\mkern 1mu} {\mkern 1mu} DC{C_1}{D_1};{\mkern 1mu} {\mkern 1mu} BC{C_1}{B_1}\)
Vậy hình lăng trụ đứng tứ giác đáy là hình thang cân có 4 mặt bên.
Đáp án: B
Bài 5: Tính thể tích của hình lăng trụ đứng có chiều cao 20cm, đáy là một tam giác vuông có các cạnh góc vuông lần lượt là 8cm và 10cm.
A. \(800c{m^3}\).
B. \(400c{m^3}\).
C. \(600c{m^3}\).
D. \(500c{m^3}\).
Phương pháp
+ Tính diện tích đáy là tam giác vuông: Sđáy = \(\frac{1}{2}\). Cạnh góc vuông . cạnh góc vuông
+ Tính thể tích: V = Sđáy . h
Lời giải
Diện tích đáy của hình lăng trụ đứng là:\(\frac{1}{2}.8.10 = 40c{m^3}\)
Thể tích của hình lăng trụ đứng là: \(40.20 = 800{\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)\)
Vậy thể tích của hình lăng trụ đứng là \(800{\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)\).
Đáp án: A
Bài 6: Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước \(3cm,{\mkern 1mu} {\mkern 1mu} 8cm\). Chiều cao của hình lăng trụ đứng là 2cm. Diện tích xung quanh của hình lăng trụ đứng là
A. \(44c{m^2}\).
B. \(24c{m^2}\).
C. \(48c{m^2}\).
D. \(22c{m^2}\).
Phương pháp
+ Tính chu vi đáy là hình chữ nhật
+ Tính Sxq = chu vi đáy . chiều cao
Lời giải
Chu vi đáy của hình lăng trụ đứng là: \(\left( {8 + 3} \right).2 = 22\left( {cm} \right)\)
Diện tích xung quanh của hình lăng trụ đứng là: \({S_{xq}} = C.h = 22.2 = 44{\mkern 1mu} {\mkern 1mu} \left( {c{m^2}} \right)\)
Vậy diện tích xung quanh của hình lăng trụ đứng là \(44{\mkern 1mu} {\mkern 1mu} \left( {c{m^2}} \right)\)
Đáp án: A
Bài 7: Cho hình lăng trụ đứng có diện tích xung quanh bằng 336 cm2, chiều cao 14 cm. Khi đó, chu vi đáy của hình lăng trụ đứng là:
A. 12cm.
B. 24cm.
C. 36cm.
D. 48cm.
Phương pháp
Từ công thức Sxq = Chu vi đáy . chiều cao suy ra chu vi đáy
Lời giải
Chu vi đáy của hình lăng trụ đứng đó là:
C = Sxq : h = 336 : 14 = 24 (cm)
Đáp án: B
Bài 8: Tính diện tích xung quanh và thể tích của hình lăng trụ ABC.DEF?
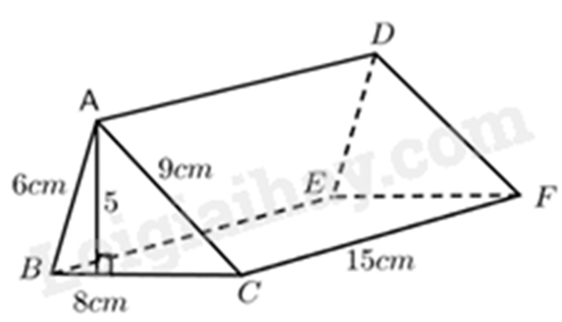
Phương pháp
Sử dụng công thức tính diện tích xung quanh và thể tích hình lăng trụ:
Sxq = Cđáy.chiều cao.
V = Sđáy.chiều cao.
Lời giải
Tính diện tích xung quanh của hình lăng trụ ABC.DEF là:
\({S_{xq}} = \left( {6 + 9 + 8} \right).15 = 345\left( {c{m^2}} \right)\)
Thể tích của hình lăng trụ ABC.DEF là:
\(V = \left( {5.8} \right):2.15 = 300\left( {c{m^3}} \right)\)
Bài 9: Một cái bục hình lăng trụ đứng tứ giác có kích thước như hình vẽ bên.
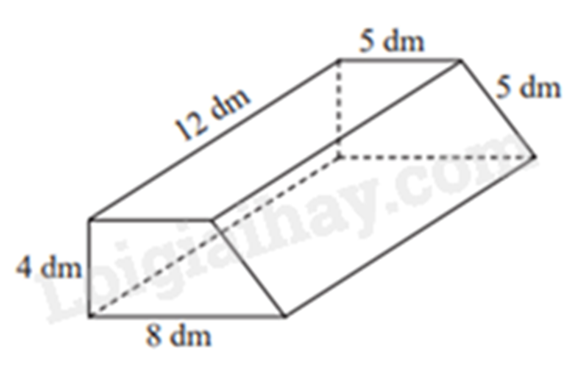
a) Tính diện tích xung quanh hình lăng trụ.
b) Người ta muốn sơn tất cả các mặt của cái bục trừ mặt nằm dưới đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
Phương pháp
a) Sử dụng công thức tính diện tích xung quanh của hình lăng trụ: Sxq = Cđáy . h.
b) Tính diện tích hai đáy.
Tính diện tích cần sơn (gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới)).
Chi phí bằng diện tích cần sơn . 25 nghìn đồng.
Lời giải
a) Diện tích xung quanh chiếc hộp là:
Sxq = Cđáy . h = (4 + 5 + 5 + 8) . 12 = 264 (dm2)
Diện tích 2 đáy là:
S2đáy = (5 + 8). 4 : 2 . 2 = 52 (dm2)
Các mặt cần sơn gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới) nên diện tích phần cần sơn là:
264 + 52 – 8.12 = 220 (dm2) = 2,2 (m2)
Do đó chi phí để sơn là:
2,2 . 25 = 55 (nghìn đồng).
Bài 10: Tính thể tích phần không gian của một ngôi nhà dạng một lăng trụ đứng theo các kích thước đã cho trong hình.
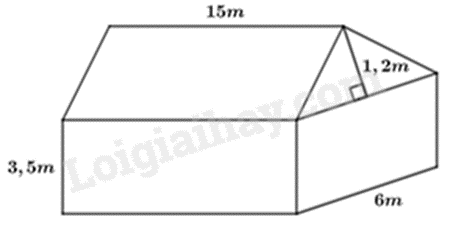
Phương pháp
Tính tổng của thể tích hình lăng trụ và thể tích hình hộp chữ nhật.
Lời giải
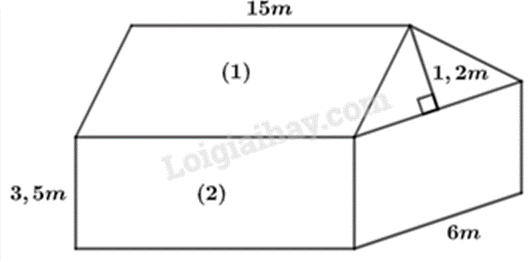
Theọ hình vẽ, ngôi nhà gồm hai phần: một phần là lăng trụ đứng có đáy là tam giác cân cạnh đáy bằng 6m, chiều cao đáy 1,2m, chiều cao lăng trụ bằng 15m; phần còn lại là hình hộp chữ nhật có kích thước đáy là 6m và 15m, chiều cao 3,5m.
Thể tích hình lăng trụ tam giác là:
\({V_1} = \frac{1}{2}.6.1,2.15 = 54\left( {{m^3}} \right)\)
Thể tích hình hộp chữ nhật là:
\({V_2} = 6.15.3,5 = 315\left( {{m^3}} \right)\)
Thể tích phần không gian bên trong của cả ngôi nhà là:
\(V = {V_1} + {V_2} = 54 + 315 = 369\left( {{m^3}} \right)\)
Thể tích phần không gian của ngôi nhà là \(369\left( {{m^3}} \right)\)
Bài 11: Người ta đào một đoạn mương dài 20 m, sâu 1,5 m. Bề mặt của mương rộng 1,8 m và đáy mương rộng 1,2 m. Tính thể tích khối đất phải đào.
Phương pháp
- Để tính diện tích hình thang, ta lấy chiều dài 2 cạnh đáy cộng lại với nhau, sau đó lấy kết quả đó nhân cho chiều cao rồi chia cho 2.
- Để tính diện tích hình lăng trụ đứng tứ giác, ta lấy diện tích đáy nhân với chiều cao.
Lời giải
Gọi đoạn mương có dạng hình lăng trụ đứng tứ giác BCC’B’.ADD’A’ có đáy là hình thang BCC’B’ (như hình vẽ).
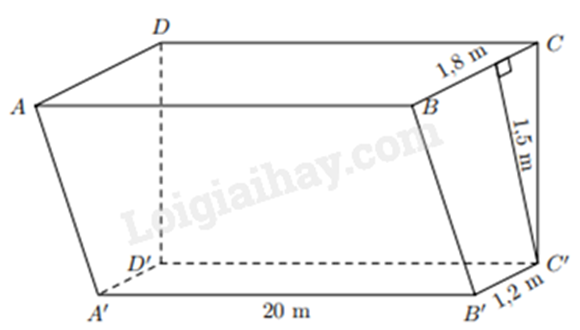
Diện tích đáy hình thang BCC’B’ là:
\(\frac{{1,2 + 1,8}}{2}.1,5 = 2,25{\mkern 1mu} \left( {{m^2}} \right)\)
Thể tích khối đất phải đào là:
\(V = 2,25.20 = 45\;({m^3})\)
Vậy thể tích khối đất phải đào là \(45\;{m^3}\).
Bài 12: Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng 6 m. Đường cao của đáy (là chiều rộng của nhà kho) bằng 5 m. Các cạnh đáy của hình thang vuông dài 3 m và 4 m. Tính thể tích của nhà kho.
Phương pháp
Sử dụng công thức tính diện tích hình thang để tính diện tích đáy.
\({S_{hthang}} = \frac{1}{2}\). tổng hai đáy. chiều cao
Sử dụng công thức tính thể tích hình lăng trụ để tính thể tích kho.
\(V = \) Sđáy . chiều cao
Lời giải
Gọi nhà kho có dạng hình lăng trụ đứng ABCD.A’B’C’D’.
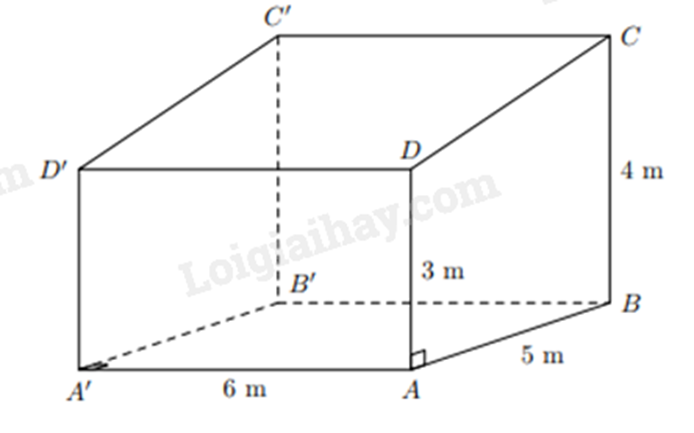
Diện tích đáy hình lăng trụ là:
\({S_{ABCD}} = \frac{1}{2}.(3 + 4).5 = 17,5(c{m^2})\)
Thể tích nhà kho là:
\({V_{kho}}{\rm{\;}} = {S_{ABCD}}.AA' = 17,5.6 = 105(c{m^3})\)
Vậy thể tích nhà kho là \(105c{m^3}\).
Bài 13: Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
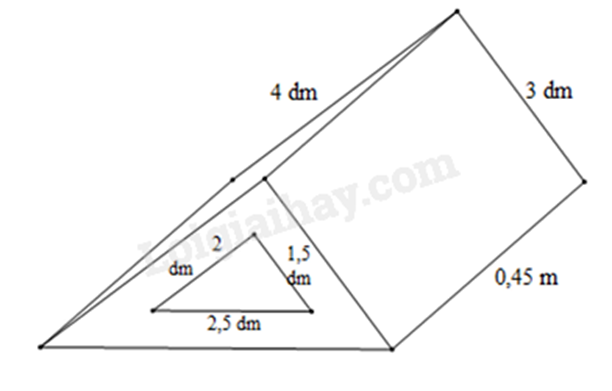
a) Tính thể tích của khối gỗ.
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Phương pháp
a) - Thể tính của khối gỗ bằng = thể tích khối gỗ khi chưa khoét - thể tích khối gỗ bị khoét.
- Công thức tính diện tích tam giác vuông = tích hai cạnh góc vuông : 2
- \(V = Sh\)
(V: Thể tích hình lăng trụ đứng tam giác; S: Diện tích đáy; h: Chiều cao)
b) - Đổi về cùng đơn vị đo.
- Tính diện tích xung quanh bên ngoài của khối gỗ.
- Diện tích xung quanh bên trong của khối gỗ.
- Tính diện tích đáy của khối gỗ sau khi khoát lỗ.
- Công thức tính diện tích xung quanh hình lăng trụ đứng tam giác = chu vi đáy x chiều cao.
- Công thức tính diện tích hình tam giác vuông = tích hai cạnh góc vuông : 2
Lời giải
a) Đổi \(0,45m = 4,5dm\).
Thể tích của khối gỗ là:
\(\frac{{4.3}}{2}.4,5 - \frac{{2.1,5}}{2}.4,5 = 20,25(d{m^3})\).
b) Đổi: \(0,5m = 5dm\)
Diện tích xung quanh bên ngoài khối gỗ là:
\((3 + 4 + 5).4,5 = 54(d{m^2})\).
Diện tích xung quanh của cái lỗ là:
\((2 + 1,5 + 2,5).4,5 = 27(d{m^2})\).
Diện tích hai đáy của khối gỗ sau khi khoét lỗ là:
\(\left( {\frac{1}{2}.3.4 - \frac{1}{2}.1,5.2} \right).2 = 9(d{m^2})\)
Diện tích bề mặt cần sơn là:
\(54 + 27 + 9 = 90\left( {d{m^2}} \right) = 0,9{m^2}\)
Vậy diện tích cần sơn là 0,9 mét vuông.
Các bài khác cùng chuyên mục
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8
- Dạng bài hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Ôn hè Toán 7 lên 8
- Dạng bài hình hộp chữ nhật và hình lập phương - Ôn hè Toán 7 lên 8
- Đề ôn hè Toán 7 lên 8 - Đề 10
- Dạng bài tính chất ba đường trung trực, trung tuyến, đường cao, phân giác của tam giác - Ôn hè Toán 7 lên 8
- Dạng bài đường trung trực của một đoạn thẳng - Ôn hè Toán 7 lên 8












Danh sách bình luận