Đề ôn hè Toán 7 lên 8 - Đề 6

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Giá trị của \(x\) trong biểu thức  \(\frac{1}{7} - x = \frac{3}{4}\) là

A. \(x =  - \frac{{17}}{{28}}\).

B. \(x = \frac{{17}}{{28}}\).

C. \(\frac{4}{{11}}\).

D. \(x = \frac{{ - 2}}{3}\).

Câu 2: Căn bậc hai số học của 121 là

A. -11.

B. 11.

C. 11 và -11.

D. \({11^2}\).

Câu 3: Kết quả của phép tính \(\left| { - 7} \right|.( - 2)\) là

A. -14.

B. -49.

C. 49.

D. 14.

Câu 4: Cho hình lăng trụ đứng tam giác ABC.DEF (hình vẽ), biết AB = 4cm, AC = 3cm, BE = 6cm.  Thể tích hình lăng trụ đó bằng

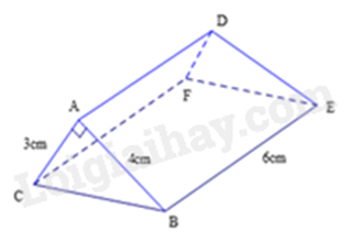
A. \(20c{m^3}\).

B. \(36c{m^3}\).

C. \(26c{m^3}\).

D. \(9c{m^3}\).

Câu 5: Nếu MN // a và MK // a thì theo tiên đề Euclid:

A. Ba điểm M, N, K tạo thành tam giác.

B. MN song song MK.

C. Ba điểm M, N, K cùng nằm trên một đường thẳng.

D. MN vuông góc MK.

Câu 6: Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 45^\circ \), số đo \(\widehat {yOz}\) bằng

A. \(45^\circ \).

B. \(55^\circ \).

C. \(105^\circ \).

D. \(135^\circ \).

Câu 7: Biểu đồ sau đây cho biết môn thể thao yêu thích nhất của các bạn học sinh khối 7 một trường THCS.

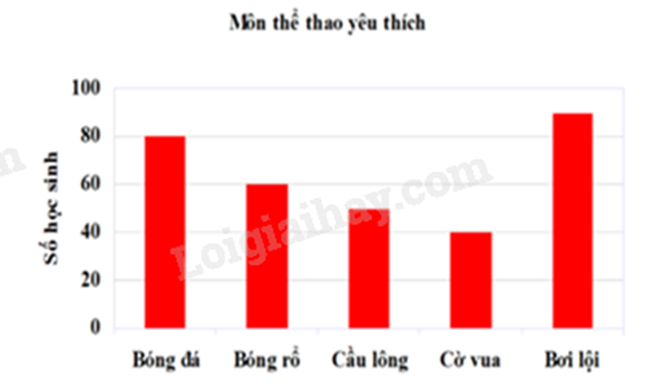
Môn thể thao được yêu thích nhất là:

A. Bóng đá.

B. Bóng rổ.

C. Cầu lông.

D. Bơi lội.

Câu 8: Đội múa có 1 bạn nam và 5 bạn nữ. Chọn ngẫu nhiên 1 bạn để phỏng vấn. Biết mỗi bạn đều có khả năng được chọn. Xác suất của biến cố “Bạn được chọn là nam”.

A. 1.

B. \(\frac{1}{6}\).

C. \(\frac{5}{6}\).

D. \(\frac{1}{2}\).

Câu 9: Biểu thức đại số biểu thị: “Tổng các bình phương của \(x\) và \(y\)” là

A. \(x + y\).

B. \({\left( {x + y} \right)^2}\).

C. \({x^2} + {y^2}\).

D. \({x^2}{y^2}\).

Câu 10: Tam giác ABC có G là trọng tâm, AM là đường trung tuyến, ta có:

A. AG =\(\frac{1}{3}\)AM.

B. AG =\(\frac{2}{3}\)AM.

C. AG =\(\frac{1}{2}\)AM.

D. AG =\(\frac{3}{2}\)AM.

Câu 11: Cho \(\Delta ABC\) có \(\widehat A = 80^\circ ;\widehat B = 45^\circ \), so sánh các cạnh của \(\Delta ABC\) ta được

A. BC > AC > AB.

B. BC > AB > AC.

C. AB > BC > AC.

D. AC > AB > BC.

Câu 12: Cho đường thẳng MN . Gọi I là một điểm nằm trên đường trung trực của đoạn thẳng MN và IM = 8cm. Khi đó độ dài đoạn IN bằng.

A. IN = 8cm.

B. IN = 4cm.

C. IN = 16cm.

D. IN = 3cm.

Phần tự luận (7 điểm)

Bài 1. (1 điểm) a) Thực hiện phép tính \(\,\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right)\).

b) Tìm x, biết \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\).

Bài 2. (2 điểm)

1. Để làm xong một công việc trong 5 giờ cần 12 công nhân. Nếu số công nhân tăng thêm 8 người thì thời gian hoàn thành công việc giảm được mấy giờ? (Giả sử năng suất làm việc của mỗi công nhân là như nhau)

2. Một khu vườn có dạng hình chữ nhật có chiều dài \(a\) (m), chiều rộng ngắn hơn chiều dài 8 (m). Trên khu vườn ấy, bác An đào một cái ao hình vuông có cạnh là b (m) (b < a – 8).

a) Viết biểu thức biểu thị diện tích còn lại của khu vườn đó.

b) Tính diện tích còn lại của khu vườn đó khi a = 50, b = 10.

Bài 3. (1 điểm) Cho hai đa thức: \(P\left( x \right) = 4{x^2} + 2x + 1\) và \(Q(x) = 2x - 1\).

a) Tính \(P\left( x \right) + Q\left( x \right)\).

b) Tìm đa thức \(A\left( x \right)\)sao cho \(A\left( x \right) + 2.Q\left( x \right) = P\left( x \right)\).

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A. Tia phân giác của \(\widehat B\) cắt AC tại E. Từ E kẻ EH vuông góc với BC tại H.

a) Chứng minh: \(\Delta ABE = \Delta HBE\,.\)

b Chứng minh BE là đường trung trực của đoạn thẳng AH.

c) Kẻ \(AD \bot BC\,\,(D \in BC)\). Chứng minh AH là tia phân giác của \(\widehat {DAC}\).

Bài 5. (0,5 điểm) Tổ I của lớp 7A có 5 học sinh nữ là: Ánh, Châu, Hương, Hoa, Ngân và 5 học sinh nam là: Bình, Dũng, Hùng, Huy, Việt. Chọn ra ngẫu nhiên một học sinh trong Tổ I của lớp 7A. Tính xác suất của biến cố sau: “Học sinh được chọn ra là học sinh nữ”.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Giá trị của \(x\) trong biểu thức  \(\frac{1}{7} - x = \frac{3}{4}\) là

A. \(x =  - \frac{{17}}{{28}}\).

B. \(x = \frac{{17}}{{28}}\).

C. \(\frac{4}{{11}}\).

D. \(x = \frac{{ - 2}}{3}\).

Phương pháp

Chuyển vế để tìm \(x\).

Lời giải

Ta có:

\(\begin{array}{l}\frac{1}{7} - x = \frac{3}{4}\\x = \frac{1}{7} - \frac{3}{4}\\x =  - \frac{{17}}{{28}}\end{array}\)

Đáp án: A

Câu 2: Căn bậc hai số học của 121 là

A. -11.

B. 11.

C. 11 và -11.

D. \({11^2}\).

Phương pháp

Căn bậc hai số học của a là \(\sqrt a \).

Lời giải

Căn bậc hai số học của \(121\) là \(\sqrt {121}  = 11\).

Đáp án: B

Câu 3: Kết quả của phép tính \(\left| { - 7} \right|.( - 2)\) là

A. -14.

B. -49.

C. 49.

D. 14.

Phương pháp

Tính \(\left| A \right|\) rồi tính phép tính.

Lời giải

\(\left| { - 7} \right|.\left( { - 2} \right) = 7.\left( { - 2} \right) =  - 14\).

Đáp án: A

Câu 4: Cho hình lăng trụ đứng tam giác ABC.DEF (hình vẽ), biết AB = 4cm, AC = 3cm, BE = 6cm.  Thể tích hình lăng trụ đó bằng

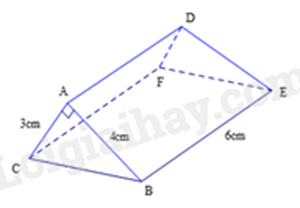
A. \(20c{m^3}\).

B. \(36c{m^3}\).

C. \(26c{m^3}\).

D. \(9c{m^3}\).

Phương pháp

Thể tích của hình lăng trụ đứng: V = S_đáy.chiều cao.

Lời giải

Diện tích đáy của hình lăng trụ đứng là: \(S = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)

Thể tích của hình lăng trụ đứng là: \(V = S.h = 6.6 = 36\left( {c{m^3}} \right)\).

Đáp án: B

Câu 5: Nếu MN // a và MK // a thì theo tiên đề Euclid:

A. Ba điểm M, N, K tạo thành tam giác.

B. MN song song MK.

C. Ba điểm M, N, K cùng nằm trên một đường thẳng.

D. MN vuông góc MK.

Phương pháp

Sử dụng kiến thức về tiên đề Euclid: qua một điểm, chỉ có một đường thẳng đi qua nó song song với đường thẳng đã cho.

Lời giải

Vì MN // a và MK // a mà qua M chỉ có một đường thẳng song song với a nên MN trùng với MK hay M, N, K cùng nằm trên một đường thẳng.

Đáp án: C

Câu 6: Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 45^\circ \), số đo \(\widehat {yOz}\) bằng

A. \(45^\circ \).

B. \(55^\circ \).

C. \(105^\circ \).

D. \(135^\circ \).

Phương pháp

Hai góc kề bù thì có tổng số đo bằng \(180^\circ \).

Lời giải

Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \).

Suy ra \(\widehat {yOz} = 180^\circ  - \widehat {xOy} = 180^\circ  - 45^\circ  = 135^\circ \).

Đáp án: D

Câu 7: Biểu đồ sau đây cho biết môn thể thao yêu thích nhất của các bạn học sinh khối 7 một trường THCS.

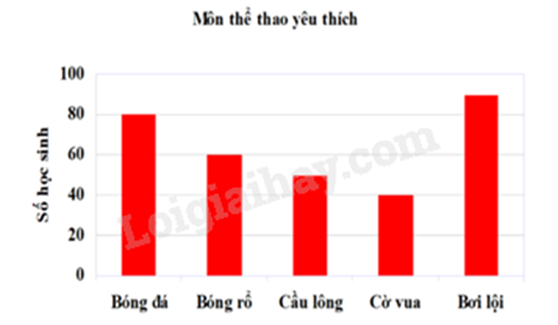
Môn thể thao được yêu thích nhất là:

A. Bóng đá.

B. Bóng rổ.

C. Cầu lông.

D. Bơi lội.

Phương pháp

Quan sát biểu đồ, xác định cột cao nhất thì môn thể thao đó được yêu thích nhất.

Lời giải

Quan sát biểu đồ ta thấy cột bơi lội cao nhất nên môn bơi lội được yêu thích nhất.

Đáp án: D

Câu 8: Đội múa có 1 bạn nam và 5 bạn nữ. Chọn ngẫu nhiên 1 bạn để phỏng vấn. Biết mỗi bạn đều có khả năng được chọn. Xác suất của biến cố “Bạn được chọn là nam”.

A. 1.

B. \(\frac{1}{6}\).

C. \(\frac{5}{6}\).

D. \(\frac{1}{2}\).

Phương pháp

Tính tổng số bạn là k.

Vì mỗi bạn có khả năng được chọn như nhau nên khả năng chọn được bạn nam là \(\frac{1}{k}\).

Lời giải

Có tổng 1 + 5 = 6 bạn.

Vì mỗi bạn có khả năng được chọn như nhau nên khả năng chọn được bạn nam là \(\frac{1}{6}\).

Đáp án: B

Câu 9: Biểu thức đại số biểu thị: “Tổng các bình phương của \(x\) và \(y\)” là

A. \(x + y\).

B. \({\left( {x + y} \right)^2}\).

C. \({x^2} + {y^2}\).

D. \({x^2}{y^2}\).

Phương pháp

Biểu diễn theo yêu cầu.

Lời giải

Bình phương của \(x\) là \({x^2}\).

Bình phương của \(y\) là \({y^2}\).

Do đó tổng các bình phương của \(x\) và \(y\) là \({x^2} + {y^2}\).

Đáp án: C

Câu 10: Tam giác ABC có G là trọng tâm, AM là đường trung tuyến, ta có:

A. AG =\(\frac{1}{3}\)AM.

B. AG =\(\frac{2}{3}\)AM.

C. AG =\(\frac{1}{2}\)AM.

D. AG =\(\frac{3}{2}\)AM.

Phương pháp

Dựa vào tính chất của đường trung tuyến: khoảng cách từ đỉnh đến trọng tâm bằng \(\frac{2}{3}\) độ dài đường trung tuyến từ đỉnh đó.

Lời giải

Vì G là trọng tâm, AM là đường trung tuyến của tam giác ABC nên \(AG = \frac{2}{3}AM\).

Đáp án: B

Câu 11: Cho \(\Delta ABC\) có \(\widehat A = 80^\circ ;\widehat B = 45^\circ \), so sánh các cạnh của \(\Delta ABC\) ta được

A. BC > AC > AB.

B. BC > AB > AC.

C. AB > BC > AC.

D. AC > AB > BC.

Phương pháp

Sử dụng tổng ba góc trong tam giác bằng \(180^\circ \) nên tính được góc C.

Sử dụng mối quan hệ giữa cạnh và góc trong tam giác, góc nào lớn hơn thì cạnh đối của góc đó lớn hơn.

Lời giải

Áp dụng định lí tổng ba góc trong tam giác vào \(\Delta ABC\), ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \)

suy ra \(\widehat C = 180^\circ  - \widehat A - \widehat B = 180^\circ  - 80^\circ  - 45^\circ  = 55^\circ \).

Vì \(80^\circ  > 55^\circ  > 45^\circ \) nên \(\widehat A > \widehat C > \widehat B\), do đó \(BC > AB > AC\).

Đáp án: B

Câu 12: Cho đường thẳng MN . Gọi I là một điểm nằm trên đường trung trực của đoạn thẳng MN và IM = 8cm. Khi đó độ dài đoạn IN bằng.

A. IN = 8cm.

B. IN = 4cm.

C. IN = 16cm.

D. IN = 3cm.

Phương pháp

Khoảng cách từ các điểm thuộc đường trung trực với hai đầu mút là bằng nhau.

Lời giải

Vì I là điểm nằm trên đường trung trực của đoạn thẳng MN nên IM = IN = 8cm.

Đáp án: A

Phần tự luận.

Bài 1. (1 điểm) a) Thực hiện phép tính \(\,\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right)\).

b) Tìm x, biết \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\).

Phương pháp

a) Thực hiện lần lượt phép nhân đến phép cộng.

b) Chuyển vế để tìm \(x\).

Lời giải

a) \(\,\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right)\)\( = \frac{2}{3} + \frac{3}{5} = \frac{{19}}{{15}}\)

b) \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\)

           \(\frac{2}{3}.x = \frac{4}{9} - \frac{1}{3}\)

           \(\frac{2}{3}.x = \frac{1}{9}\)

               \(\begin{array}{l}x = \frac{1}{9}:\frac{2}{3}\\x = \frac{1}{6}\end{array}\)

Vậy \(x = \frac{1}{6}\).

Bài 2. (2 điểm)

1. Để làm xong một công việc trong 5 giờ cần 12 công nhân. Nếu số công nhân tăng thêm 8 người thì thời gian hoàn thành công việc giảm được mấy giờ? (Giả sử năng suất làm việc của mỗi công nhân là như nhau)

2. Một khu vườn có dạng hình chữ nhật có chiều dài \(a\) (m), chiều rộng ngắn hơn chiều dài 8 (m). Trên khu vườn ấy, bác An đào một cái ao hình vuông có cạnh là b (m) (b < a – 8).

a) Viết biểu thức biểu thị diện tích còn lại của khu vườn đó.

b) Tính diện tích còn lại của khu vườn đó khi a = 50, b = 10.

Phương pháp

1. Tính số công nhân sau khi tăng thêm 8 người.

Gọi x (giờ) là thời gian hoàn thành công việc với 20 công nhân (x > 0)

Chứng minh số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch với nhau.

Suy ra tỉ lệ tương ứng giữa hai tỉ lệ.

Giải để tìm \(x\).

Tính số giờ được giảm.

2.

a) Viết biểu thức biểu thị chiều rộng, diện tích khu vườn, diện tích cái ao.

Suy ra biểu thức biểu thị diện tích còn lại của khu vườn.

b) Thay a = 50, b = 10 vào biểu thức để tính giá trị.

Lời giải

1. Số công nhân sau khi tăng thêm 8 người là 12 + 8 = 20 (công nhân)

Gọi x (giờ) là thời gian hoàn thành công việc với 20 công nhân (x > 0)

Vì cùng hoàn thành một công việc nên số công nhân và thời gian hoàn thành công việc là 2 đại lượng tỉ lệ nghịch với nhau.

Ta có \(\frac{5}{x} = \frac{{20}}{{12}}\)

suy ra x = \(\frac{{5.12}}{{20}} = 3\)

Vậy sau khi tăng thêm 8 công nhân thì thời gian hoàn thành công việc được giảm là 5 – 3 = 2 (giờ)

2. a) Chiều rộng hình chữ nhật là: a – 8 (m)

Diện tích hình chữ nhật là: \(a\left( {a - 8} \right)\)\(\left( {{m^2}} \right)\)

Diện tích hình vuông là: \({b^2}\)\(\left( {{m^2}} \right)\)

Vậy biểu thức biểu thị diện tích còn lại của khu vườn đó là: \(a\left( {a - 8} \right) - {b^2}\)\(\left( {{m^2}} \right)\)

b) Với a = 50, b = 10, diện tích còn lại của khu vườn đó là:

 \(a\left( {a - 8} \right) - {b^2} = 50(50 - 8) - {10^2} = 2000\)\(\left( {{m^2}} \right)\)

Bài 3. (1 điểm) Cho hai đa thức: \(P\left( x \right) = 4{x^2} + 2x + 1\) và \(Q(x) = 2x - 1\).

a) Tính \(P\left( x \right) + Q\left( x \right)\).

b) Tìm đa thức \(A\left( x \right)\)sao cho \(A\left( x \right) + 2.Q\left( x \right) = P\left( x \right)\).

Phương pháp

a) Để cộng đa thức một biến, ta bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc (theo hàng ngang).

b) Để tìm đa thức chưa biết trong một đẳng thức, ta làm như sau:

- Xác định vai trò của đa thức chưa biết (chẳng hạn, đóng vai trò số hạng chưa biết, số bị trừ, số trừ, …)

- Áp dụng quy tắc dấu ngoặc, quy tắc chuyển vế và quy tắc cộng, trừ đa thức một biến để biến đổi.

Lời giải

a) \(P\left( x \right) + Q(x) = (4{x^2} + 2x + 1){\rm{  +  (}}2x - 1)\)

\(\begin{array}{l} = 4{x^2} + 2x + 1 + 2x - 1\\ = 4{x^2} + (2x + 2x) + (1 - 1)\\ = 4{x^2} + 4x\end{array}\)

b) \(A\left( x \right) + 2.Q\left( x \right) = P\left( x \right)\)

\(\begin{array}{l}A\left( x \right) = P\left( x \right) - 2.Q\left( x \right)\\A\left( x \right) = \left( {4{x^2} + 2x + 1} \right) - 2.\left( {2x - 1} \right)\\A\left( x \right) = 4{x^2} + 2x + 1 - 4x + 2\\A\left( x \right) = 4{x^2} - 2x + 3\end{array}\)

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A. Tia phân giác của \(\widehat B\) cắt AC tại E. Từ E kẻ EH vuông góc với BC tại H.

a) Chứng minh: \(\Delta ABE = \Delta HBE\,.\)

b Chứng minh BE là đường trung trực của đoạn thẳng AH.

c) Kẻ \(AD \bot BC\,\,(D \in BC)\). Chứng minh AH là tia phân giác của \(\widehat {DAC}\).

Phương pháp

a) Chứng minh \(\Delta ABE = \Delta HBE\) (cạnh huyền - góc nhọn)

b) Chứng minh BA = BH và EA = EH nên B và E thuộc đường trung trực của AH.

c) Chứng minh AH là tia phân giác của \(\widehat {DAC}\)

Chứng minh \(\widehat {DAH} = \;\widehat {EHA}\;\) và \(\widehat {EAH} = \;\widehat {EHA}\) nên \(\widehat {EAH} = \;\widehat {DAH}\) hay AH là tia phân giác của \(\widehat {DAC}\).

Lời giải

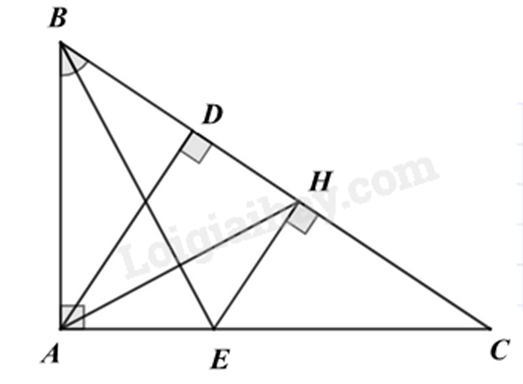
a) Chứng minh \(\Delta ABE = \Delta HBE\)

Xét 2 tam giác \(\Delta ABE\) và \(\Delta HBE\) ta có:

\(\widehat {BAE} = \widehat {BHE} = 90^\circ \left( {gt} \right)\)

BE cạnh chung

\(\widehat {ABE} = \widehat {DBE}\) (gt)

Suy ra \(\Delta ABE = \Delta HBE\) (cạnh huyền - góc nhọn)

b) Chứng minh BE là đường trung trực của đoạn thẳng AH

Vì \(\Delta ABE = \Delta HBE\) (cmt) nên:

BA = BH (hai cạnh tương ứng) nên B thuộc đường trung trực của AH

EA = EH (hai cạnh tương ứng) nên E thuộc đường trung trực của AH

Vậy BE là đường trung trực của đoạn thẳng AH.

c) Chứng minh AH là tia phân giác của \(\widehat {DAC}\)

Ta có: AD // EH (cùng vuông góc với BC) suy ra \(\widehat {DAH} = \;\widehat {EHA}\;\) (hai góc so le trong)

Vì EA = EH (cmt) nên tam giác EAH cân tại E suy ra \(\widehat {EAH} = \;\widehat {EHA}\)

Vậy \(\widehat {EAH} = \;\widehat {DAH}\) hay AH là tia phân giác của \(\widehat {DAC}\).

Bài 5. (0,5 điểm) Tổ I của lớp 7A có 5 học sinh nữ là: Ánh, Châu, Hương, Hoa, Ngân và 5 học sinh nam là: Bình, Dũng, Hùng, Huy, Việt. Chọn ra ngẫu nhiên một học sinh trong Tổ I của lớp 7A. Tính xác suất của biến cố sau: “Học sinh được chọn ra là học sinh nữ”.

Phương pháp

Tính số kết quả có thể xảy ra.

Tính số kết quả thuận lợi cho biến cố.

Xác suất của biến cố = số kết quả thuận lợi : số kết quả có thể.

Lời giải

Tập hợp có thể xảy ra đối với học sinh được chọn ra là:

E = {Ánh; Châu; Hương; Hoa; Ngân; Bình; Dũng; Hùng; Huy; Việt}.

Số phần tử của tập hợp E là 10 phần tử.

Có 5 kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nữ” là: Ánh, Châu, Hương, Hoa, Ngân.

Do đó xác suất của biến cố “Học sinh được chọn ra là học sinh nữ” bằng \(\frac{5}{{10}} = \frac{1}{2}\).