Đề ôn hè Toán 7 lên 8 - Đề 2

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Số 9 là căn bậc hai số học của số

A. -81.

B. 81.

C. 3.

D. -3.

Câu 2: Làm tròn số 35,3256 với độ chính xác 0,05 là

A. 35,3.

B. 35,33.

C. 35,32.

D. 35,325.

Câu 3: Các giá trị của \(x\) thoả mãn \(\left| x \right| - 1 = 3\) là

A. \(x = 4\).

B. \(x = 4;x =  - 4\).

C. \(x = 2;x =  - 2\).

D. \(x =  - 4\).

Câu 4: Giá trị của \(x\) trong đẳng thức \(\frac{{ - 1}}{5} = \frac{x}{{ - 15}}\) là

A. 75.

B. -3.

C. 3.

D. -75.

Câu 5: Tam giác ABC có \(\widehat A = 60^\circ ;\widehat B = 35^\circ \), khi đó số đo của góc C là:

A. \(85^\circ \).

B. \(75^\circ \).

C. \(95^\circ \).

D. \(60^\circ \).

Câu 6: Cho hình vẽ. Với các kí hiệu trên hình vẽ, cần thêm yếu tố nào để \(\Delta ABC = \Delta ADE\left( {g.c.g} \right)\)?

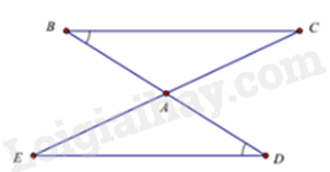
A. \(AB = AD\).

B. \(\widehat {BCA} = \widehat {AED}\).

C. \(\widehat {BCA} = \widehat {DEA}\).

D. \(AC = AE\).

Câu 7: Thu nhập bình quân lao động của Việt Nam ở một số năm trong giai đoạn từ năm 2022 đến năm 2024, thống kê như sau:

Thu nhập bình quân lao động của Việt Nam ở năm 2024 tăng so với năm 2023 là khoảng

A. 105%.

B. 5,4%.

C. 5,47%.

D. 5,48%.

Câu 8: Gieo ngẫu nhiên xúc xắc 6 mặt một lần. Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số” là:

A. \(\frac{5}{6}\).

B. \(\frac{4}{6}\).

C. \(\frac{1}{2}\).

D. \(\frac{1}{3}\).

Câu 9: Giá trị của đa thức \(F\left( x \right) = {x^2} + 4\) tại \(x =  - 2\) là:

A. -8.

B. 0.

C. 4.

D. 8.

Câu 10: Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, khẳng định nào đúng?

A. \(\widehat A > \widehat B > \widehat C\).

B. \(\widehat C > \widehat A > \widehat B\).

C. \(\widehat A < \widehat B < \widehat C\).

D. \(\widehat C < \widehat A < \widehat B\).

Câu 11: Trong các bộ ba đoạn thẳng sau đây, bộ ba đoạn thẳng nào là độ dài ba cạnh của một tam giác là:

A. 3 cm; 5 cm; 10 cm.

B. 4 cm; 5 cm; 1 cm.

C. 5 cm; 3 cm; 2 cm.

D. 5 cm; 3 cm; 6 cm.

Câu 12: Cho \(\Delta ABC\) cân tại A và có \(\widehat A = 80^\circ \). Số đo góc đáy của tam giác đó bằng

A. \(50^\circ \).

B. \(90^\circ \).

C. \(40^\circ \).

D. \(80^\circ \).

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm)

a) Tính giá trị của biểu thức sau: \({\left( { - 2} \right)^3} + 1\frac{1}{3}\left| {2,5} \right| - \sqrt {49} :\frac{7}{5}\).

b) Tìm \(x\), biết: \(\left| {2x - 1} \right| - \frac{1}{2} = \frac{1}{3}\).

c) Tìm hai số \(x\) và \(y\), biết \(\frac{x}{3} = \frac{y}{2}\) và \(2x + y = 40\).

Bài 2. (2 điểm) Cho hai đa thức:

\(P\left( x \right) = 3 + 2{x^2} - 5x - 1 + 5{x^3} + 7x\)

\(Q\left( x \right) =  - 9x + 5{x^3} + {x^2} + 2 + x\).

a) Thu gọn và sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.

b) Tính \(G\left( x \right) = P\left( x \right) + Q\left( x \right)\); \(H\left( x \right) = P\left( x \right) - Q\left( x \right)\).

c) Tìm nghiệm của đa thức \(H\left( x \right)\).

Bài 3. (1 điểm) Trong một buổi lao động trồng cây, ba bạn Hiếu, An và Khang trồng được số cây tỉ lệ với các số 5; 3; 4. Tính số cây mỗi bạn trồng được, biết tổng số cây trồng được của ba bạn là 48 cây.

Bài 4. (2 điểm) Cho \(\Delta ABC\) vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (\(H \in BC\)). Gọi K là giao điểm của AB và HE. Chứng minh rằng:

a) \(\Delta ABE = \Delta HBE\).

b) BE là đường trung trực của đoạn thẳng AH.

c) \(\Delta BKC\) cân.

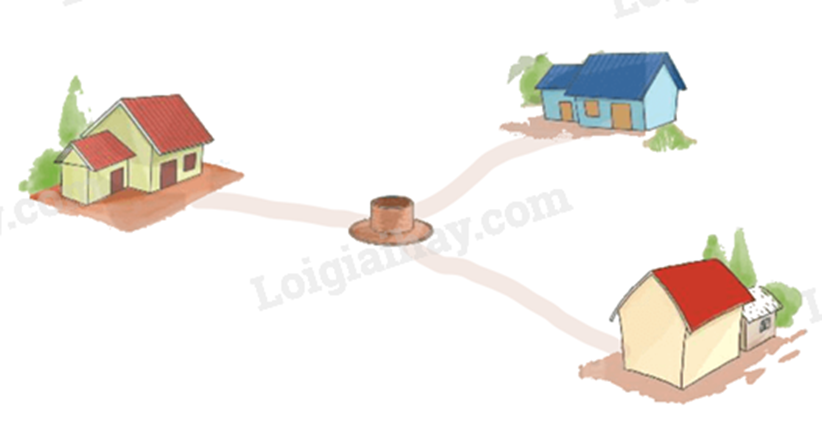
Bài 5. (0,5 điểm) Ba ngôi nhà của ba gia đình ở liền nhau trên một khu đất là ba đỉnh của tam giác nhọn. Họ muốn khoan một cái giếng chung cách đều ba ngôi nhà. Hãy giúp họ chọn địa điểm để khoan giếng.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Số 9 là căn bậc hai số học của số

A. -81.

B. 81.

C. 3.

D. -3.

Phương pháp

Số a là căn bậc hai số học của \({a^2}\).

Lời giải

Số 9 là căn bậc hai số học của \({9^2} = 81\).

Đáp án: B

Câu 2: Làm tròn số 35,3256 với độ chính xác 0,05 là

A. 35,3.

B. 35,33.

C. 35,32.

D. 35,325.

Phương pháp

Làm tròn số với độ chính xác 0,05 là làm tròn số đến hàng phần mười.

Ta thực hiện theo quy tắc làm tròn số.

Lời giải

Số 35,3256 làm tròn với độ chính xác 0,05 là: 35,3.

Đáp án: A

Câu 3: Các giá trị của \(x\) thoả mãn \(\left| x \right| - 1 = 3\) là

A. \(x = 4\).

B. \(x = 4;x =  - 4\).

C. \(x = 2;x =  - 2\).

D. \(x =  - 4\).

Phương pháp

Với \(\left| x \right| = a > 0\), ta chia hai trường hợp \(x = a\) hoặc \(x =  - a\).

Lời giải

\(\begin{array}{l}\left| x \right| - 1 = 3\\\left| x \right| = 3 + 1\\\left| x \right| = 4\end{array}\)

\(x = 4\) hoặc \(x =  - 4\).

Đáp án: B

Câu 4: Giá trị của \(x\) trong đẳng thức \(\frac{{ - 1}}{5} = \frac{x}{{ - 15}}\) là

A. 75.

B. -3.

C. 3.

D. -75.

Phương pháp

Sử dụng tính chất của tỉ lệ thức: \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).

Lời giải

\(\frac{{ - 1}}{5} = \frac{x}{{ - 15}}\)

suy ra \(5.x = \left( { - 1} \right).\left( { - 15} \right)\)

\(\begin{array}{l}5x = 15\\x = 15:5\\x = 3\end{array}\)

Đáp án: C

Câu 5: Tam giác ABC có \(\widehat A = 60^\circ ;\widehat B = 35^\circ \), khi đó số đo của góc C là:

A. \(85^\circ \).

B. \(75^\circ \).

C. \(95^\circ \).

D. \(60^\circ \).

Phương pháp

Sử dụng định lí tổng ba góc của một tam giác bằng \(180^\circ \).

Lời giải

Áp dụng định lí tổng ba góc của một tam giác vào tam giác ABC, ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \)

suy ra \(\widehat C = 180^\circ  - \widehat A - \widehat B = 180^\circ  - 60^\circ  - 35^\circ  = 85^\circ \)

Đáp án: A

Câu 6: Cho hình vẽ. Với các kí hiệu trên hình vẽ, cần thêm yếu tố nào để \(\Delta ABC = \Delta ADE\left( {g.c.g} \right)\)?

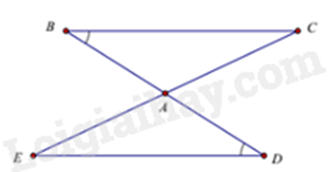
A. \(AB = AD\).

B. \(\widehat {BCA} = \widehat {AED}\).

C. \(\widehat {BCA} = \widehat {DEA}\).

D. \(AC = AE\).

Phương pháp

Xác định các yếu tố đã có trong hình vẽ để bổ sung yếu tố cần.

Lời giải

Trên hình vẽ, ta thấy \(\widehat {ABC} = \widehat {ADE}\); \(\widehat {BAC} = \widehat {DAE}\) (2 góc đối đỉnh), cạnh xen giữa của các cặp góc trên là AB và AD nên ta cần thêm AB = AD để có \(\Delta ABC = \Delta ADE\left( {g.c.g} \right)\)

Đáp án: A

Câu 7: Thu nhập bình quân lao động của Việt Nam ở một số năm trong giai đoạn từ năm 2022 đến năm 2024, thống kê như sau:

Thu nhập bình quân lao động của Việt Nam ở năm 2024 tăng so với năm 2023 là khoảng

A. 105%.

B. 5,4%.

C. 5,47%.

D. 5,48%.

Phương pháp

Xác định thu nhập bình quân năm 2023, 2024.

Thu nhập bình quân lao động của Việt Nam ở năm 2024 tăng so với năm 2023

= (thu nhập 2024 – thu nhập 2023) : thu nhập 2023 . 100%

Lời giải

Quan sát bảng thống kê, ta có thu nhập bình quân lao động ở Việt Nam năm 2023, 2024 lần lượt là 7,3; 7,7.

Thu nhập bình quân lao động của Việt Nam ở năm 2024 tăng so với năm 2023 là:

\(\frac{{7,7 - 7,3}}{{7,3}}.100\%  = 5,48\% \).

Đáp án: D

Câu 8: Gieo ngẫu nhiên xúc xắc 6 mặt một lần. Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số” là:

A. \(\frac{5}{6}\).

B. \(\frac{4}{6}\).

C. \(\frac{1}{2}\).

D. \(\frac{1}{3}\).

Phương pháp

Xác định các kết quả có thể cho biến cố, kết quả thuận lợi cho biến cố.

Xác suất của biến cố = số kết quả thuận lợi : số kết quả có thể.

Lời giải

Vì con xúc xắc có 6 mặt từ 1 đến 6 nên có 6 kết quả có thể khi gieo con xúc xắc.

Từ 1 đến 6 có 2 số là hợp số, đó là 4; 6. Do đó có 2 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số”.

Vậy xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số” là: \(\frac{2}{6} = \frac{1}{3}\).

Đáp án: D

Câu 9: Giá trị của đa thức \(F\left( x \right) = {x^2} + 4\) tại \(x =  - 2\) là:

A. -8.

B. 0.

C. 4.

D. 8.

Phương pháp

Thay giá trị của \(x\) vào đa thức để tính giá trị của đa thức.

Lời giải

Thay \(x =  - 2\) vào đa thức, ta được:

\(F\left( { - 2} \right) = {\left( { - 2} \right)^2} + 4 = 4 + 4 = 8\).

Đáp án: D

Câu 10: Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, khẳng định nào đúng?

A. \(\widehat A > \widehat B > \widehat C\).

B. \(\widehat C > \widehat A > \widehat B\).

C. \(\widehat A < \widehat B < \widehat C\).

D. \(\widehat C < \widehat A < \widehat B\).

Phương pháp

Áp dụng mối quan hệ giữa góc và cạnh đối diện: cạnh nào lớn hơn thì góc đối của nó lớn hơn.

Lời giải

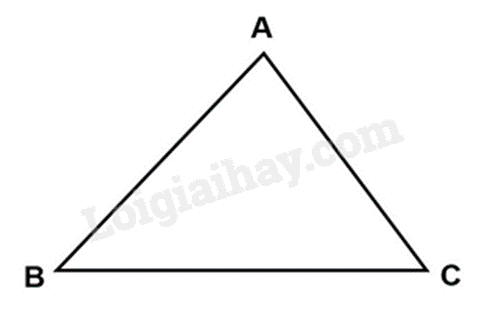
Các góc đối của các cạnh AC, BC, AB lần lượt là \(\widehat B,\widehat A,\widehat C\) nên với \(AC > BC > AB\) thì \(\widehat B > \widehat A > \widehat C\) hay \(\widehat C < \widehat A < \widehat B\).

Đáp án: D

Câu 11: Trong các bộ ba đoạn thẳng sau đây, bộ ba đoạn thẳng nào là độ dài ba cạnh của một tam giác là:

A. 3 cm; 5 cm; 10 cm.

B. 4 cm; 5 cm; 1 cm.

C. 5 cm; 3 cm; 2 cm.

D. 5 cm; 3 cm; 6 cm.

Phương pháp

Dựa vào quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.

Lời giải

Ba đoạn thẳng 3 cm; 5 cm; 10 cm không thể là độ dài ba cạnh của một tam giác vì 3 + 5 = 8 < 10.

Ba đoạn thẳng 4 cm; 5 cm; 1 cm không thể là độ dài ba cạnh của một tam giác vì 4 + 1 = 5.

Ba đoạn thẳng 5 cm; 3 cm; 2 cm không thể là  vì 3 + 2 = 5.

Ba đoạn thẳng 5 cm; 3 cm; 6 cm là độ dài ba cạnh của một tam giác vì:

5 + 3 = 8 > 6;

5 + 6 = 11 > 3;

3 + 6 = 9 > 5.

Đáp án: D

Câu 12: Cho \(\Delta ABC\) cân tại A và có \(\widehat A = 80^\circ \). Số đo góc đáy của tam giác đó bằng

A. \(50^\circ \).

B. \(90^\circ \).

C. \(40^\circ \).

D. \(80^\circ \).

Phương pháp

Sử dụng định lí tổng ba góc của tam giác và hai góc ở đáy của tam giác cân bằng nhau.

Lời giải

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta ABC\), ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(\widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - 80^\circ  = 100^\circ \).

Vì \(\Delta ABC\) cân tại A nên \(\widehat B = \widehat C = \frac{{\widehat B + \widehat C}}{2} = \frac{{100^\circ }}{2} = 50^\circ \).

Đáp án: A

Phần tự luận.

Bài 1. (1,5 điểm)

a) Tính giá trị của biểu thức sau: \({\left( { - 2} \right)^3} + 1\frac{1}{3}\left| {2,5} \right| - \sqrt {49} :\frac{7}{5}\).

b) Tìm \(x\), biết: \(\left| {2x - 1} \right| - \frac{1}{2} = \frac{1}{3}\).

c) Tìm hai số \(x\) và \(y\), biết \(\frac{x}{3} = \frac{y}{2}\) và \(2x + y = 40\).

Phương pháp

a) Tính luỹ thừa, giá trị tuyệt đối, căn bậc hai.

Đưa hỗn số về phân số để thực hiện tính toán.

b) Đưa giá trị tuyệt đối về \(\left| A \right| = B\), chia hai trường hợp \(A = B\) hoặc \(A =  - B\).

c) Quy đồng phân số \(\frac{x}{3}\) để xuất hiện \(2x\).

Sử dụng tính chất dãy tỉ số bằng nhau để tìm x, y.

Lời giải

a) \({\left( { - 2} \right)^3} + 1\frac{1}{3}\left| {2,5} \right| - \sqrt {49} :\frac{7}{5}\)

\(\begin{array}{l} =  - 8 + \frac{4}{3}.2,5 - 7.\frac{5}{7}\\ =  - 8 + \frac{4}{3}.\frac{5}{2} - 5\\ =  - 8 + \frac{{10}}{3} - 5\\ =  - 13 + \frac{{10}}{3}\\ = \frac{{ - 29}}{3}\end{array}\)

b) \(\left| {2x - 1} \right| - \frac{1}{2} = \frac{1}{3}\)

\(\begin{array}{l}\left| {2x - 1} \right| = \frac{1}{3} + \frac{1}{2}\\\left| {2x - 1} \right| = \frac{5}{6}\end{array}\)

suy ra \(2x - 1 = \frac{5}{6}\) hoặc \(2x - 1 = \frac{{ - 5}}{6}\)

TH1: \(2x - 1 = \frac{5}{6}\)

          \(\begin{array}{l}2x = \frac{5}{6} + 1\\2x = \frac{{11}}{6}\\x = \frac{{11}}{6}:2\\x = \frac{{11}}{{12}}\end{array}\)

TH2: \(2x - 1 = \frac{{ - 5}}{6}\)

          \(\begin{array}{l}2x = \frac{{ - 5}}{6} + 1\\2x = \frac{1}{6}\\x = \frac{1}{6}:2\\x = \frac{1}{{12}}\end{array}\)

Vậy \(x = \frac{{11}}{{12}};x = \frac{1}{{12}}\)

c) Vì \(\frac{x}{3} = \frac{y}{2}\) nên \(\frac{{2x}}{6} = \frac{y}{2}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{{2x}}{6} = \frac{y}{2} = \frac{{2x + y}}{{6 + 2}} = \frac{{40}}{8} = 5\)

\(\frac{{2x}}{6} = 5\) thì \(2x = 5.6\), suy ra \(x = \frac{{5.6}}{2} = 15\)

\(\frac{y}{2} = 5\) thì \(y = 5.2 = 10\)

Vậy \(x = 15;y = 10\).

Bài 2. (2 điểm) Cho hai đa thức:

\(P\left( x \right) = 3 + 2{x^2} - 5x - 1 + 5{x^3} + 7x\)

\(Q\left( x \right) =  - 9x + 5{x^3} + {x^2} + 2 + x\).

a) Thu gọn và sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.

b) Tính \(G\left( x \right) = P\left( x \right) + Q\left( x \right)\); \(H\left( x \right) = P\left( x \right) - Q\left( x \right)\).

c) Tìm nghiệm của đa thức \(H\left( x \right)\).

Phương pháp

a) Bước 1: Cộng, trừ các đơn thức cùng bậc để thu được đa thức thu gọn không chứa hai đơn thức nào cùng bậc

Bước 2: Sắp xếp đa thức trên theo lũy thừa giảm của biến.

b) Để cộng (hay trừ) hai đa thức, ta làm như sau:

Bước 1: Viết hai đa thức trong dấu ngoặc

Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc)

Bước 3: Nhóm các hạng tử đồng dạng

Bước 4: Cộng, trừ các đơn thức đồng dạng.

c) Giải tìm \(x\) để \(H\left( x \right) = 0\).

Lời giải

a) \(P\left( x \right) = 3 + 2{x^2} - 5x - 1 + 5{x^3} + 7x\)

\(\begin{array}{l}P\left( x \right) = 5{x^3} + 2{x^2} + \left( { - 5x + 7x} \right) + \left( {3 - 1} \right)\\P\left( x \right) = 5{x^3} + 2{x^2} + 2x + 2\end{array}\)

\(\begin{array}{l}Q\left( x \right) =  - 9x + 5{x^3} + {x^2} + 2 + x\\Q\left( x \right) = 5{x^3} + {x^2} + \left( { - 9x + x} \right) + 2\\Q\left( x \right) = 5{x^3} + {x^2} - 8x + 2\end{array}\)

b) \(G\left( x \right) = P\left( x \right) + Q\left( x \right)\)

\(\begin{array}{l} = 5{x^3} + 2{x^2} + 2x + 2 + 5{x^3} + {x^2} - 8x + 2\\ = \left( {5{x^3} + 5{x^3}} \right) + \left( {2{x^2} + {x^2}} \right) + \left( {2x - 8x} \right) + \left( {2 + 2} \right)\\ = 10{x^3} + 3{x^2} - 6x + 4\end{array}\)

\(H\left( x \right) = P\left( x \right) - Q\left( x \right)\)

\(\begin{array}{l} = \left( {5{x^3} + 2{x^2} + 2x + 2} \right) - \left( {5{x^3} + {x^2} - 8x + 2} \right)\\ = 5{x^3} + 2{x^2} + 2x + 2 - 5{x^3} - {x^2} + 8x - 2\\ = \left( {5{x^3} - 5{x^3}} \right) + \left( {2{x^2} - {x^2}} \right) + \left( {2x + 8x} \right) + \left( {2 - 2} \right)\\ = {x^2} + 10x\end{array}\)

c) Cho \(H\left( x \right) = 0\)

\(\begin{array}{l}{x^2} + 10x = 0\\x\left( {x + 10} \right) = 0\end{array}\)

\(x = 0\) hoặc \(x + 10 = 0\)

TH1: \(x = 0\)

TH2: \(x + 10 = 0\)

          \(x =  - 10\)

Vậy đa thức \(H\left( x \right)\) có nghiệm là \(x = 0\) và \(x =  - 10\).

Bài 3. (1 điểm) Trong một buổi lao động trồng cây, ba bạn Hiếu, An và Khang trồng được số cây tỉ lệ với các số 5; 3; 4. Tính số cây mỗi bạn trồng được, biết tổng số cây trồng được của ba bạn là 48 cây.

Phương pháp

Gọi số cây mà ba bạn Hiếu, An, Khang trồng được lần lượt là \(x,y,z\) (cây), \(x,y,z \in {\mathbb{N}^*}\).

Sử dụng tính chất dãy tỉ số bằng nhau để tính số cây.

Lời giải

Gọi số cây mà ba bạn Hiếu, An, Khang trồng được lần lượt là \(x,y,z\) (cây), \(x,y,z \in {\mathbb{N}^*}\).

Vì số cây ba bạn Hiếu, An, Khang trồng được tỉ lệ với các số 5, 3, 4 nên ta có: \(\frac{x}{5} = \frac{y}{3} = \frac{z}{4}\).

Vì tổng số cây trồng được của ba bạn là 48 cây nên ta có: \(x + y + z = 48\).

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{x}{5} = \frac{y}{3} = \frac{z}{4} = \frac{{x + y + z}}{{5 + 3 + 4}} = \frac{{48}}{{12}} = 4\)

\(\frac{x}{5} = 4\) suy ra \(x = 20\) (TMĐK)

\(\frac{y}{3} = 4\) suy ra \(y = 12\) (TMĐK)

\(\frac{z}{4} = 4\) suy ra \(z = 16\) (TMĐK)

Vậy số cây ba bạn Hiếu, An, Khang trồng được lần lượt là 20, 12, 16 cây.

Bài 4. (2 điểm) Cho \(\Delta ABC\) vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (\(H \in BC\)). Gọi K là giao điểm của AB và HE. Chứng minh rằng:

a) \(\Delta ABE = \Delta HBE\).

b) BE là đường trung trực của đoạn thẳng AH.

c) \(\Delta BKC\) cân.

Phương pháp

a) Chứng minh \(\Delta ABE = \Delta HBE\) theo trường hợp cạnh huyền – góc nhọn.

b) Chứng minh B, E cùng cách đều A và H nên BE là đường trung trực của đoạn thẳng AH.

c) Chứng minh \(\Delta BKC\) có hai cạnh bằng nhau nên là tam giác cân.

Lời giải

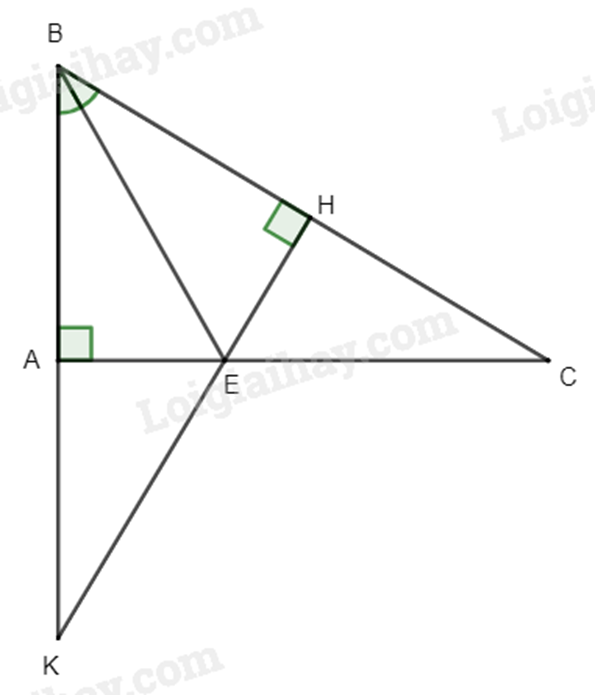
a) Xét \(\Delta ABE\) vuông tại A và \(\Delta HBE\) vuông tại H có:

BE là cạnh chung

\(\widehat {ABE} = \widehat {HBE}\left( {gt} \right)\)

Suy ra \(\Delta ABE = \Delta HBE\) (cạnh huyền – góc nhọn)

b) Ta có: BA = BH (do \(\Delta ABE = \Delta HBE\)) nên B nằm trên đường trung trực của AH (1)

Ta lại có AE = EH (do \(\Delta ABE = \Delta HBE\)) nên E nằm trên đường trung trực của AH (2)

Từ (1) và (2) suy ra BE là đường trung trực của AH.

c) Xét tam giác vuông BKH vuông tại H và tam giác BCA vuông tại A có:

BA = BH (cmt)

\(\widehat B\) chung

Do đó \(\Delta BHK = \Delta BAC\) (cạnh góc vuông – góc nhọn)

Suy ra \(BK = BC\) (hai cạnh tương ứng)

Xét \(\Delta BKC\) có \(BK = BC\) nên \(\Delta BKC\) là tam giác cân tại B.

Bài 5. (0,5 điểm) Ba ngôi nhà của ba gia đình ở liền nhau trên một khu đất là ba đỉnh của tam giác nhọn. Họ muốn khoan một cái giếng chung cách đều ba ngôi nhà. Hãy giúp họ chọn địa điểm để khoan giếng.

Phương pháp

Dựa vào tính chất giao điểm của các đường cao, đường trung tuyến, đường phân giác, đường trung trực trong tam giác để xác định giao điểm phù hợp.

Lập luận để chứng minh điểm cần tìm.

Lời giải

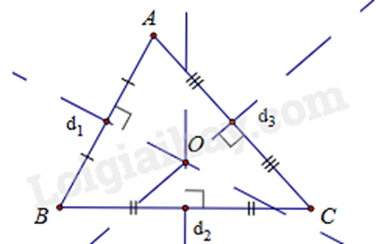
Gọi ba ngôi nhà của ba gia đình là A, B, C và O là vị trí đào giếng cách đều ba ngôi nhà.

Vì ba ngôi nhà là ba đỉnh của một tam giác nhọn, nên:

+ O cách đều A, B nên O thuộc đường trung trực của AB.

+ O cách đều B, C nên O thuộc đường trung trực của BC.

+ O cách đều A, C nên O thuộc đường trung trực của AC.

Suy ra O là giao điểm của ba đường trung trực của ba cạnh \(\Delta ABC\).