Dạng bài thực hiện phép tính - Ôn hè Toán 7 lên 8

Lý thuyết

* Quy tắc cộng, trừ hai đơn thức có cùng số mũ của biến

Để cộng (trừ) hai đơn thức có cùng số mũ của biến, ta cộng (trừ) hai hệ số với nhau và giữ nguyên phần biến.

Tổng quát: \(a{x^k} + b{x^k} = \left( {a + b} \right){x^k};a{x^k} - b{x^k} = \left( {a - b} \right){x^k}\) \(\left( {k \in {\mathbb{N}^*}} \right)\)

* Quy tắc cộng, trừ đa thức một biến

Để cộng, trừ đa thức một biến, ta có thể thực hiện 1 trong 2 cách sau:

Cách 1. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc (theo hàng ngang)

Cách 2. Sắp xếp các hạng tử của các đa thức theo luỹ thừa giảm (tăng) của biến rồi đặt tính cộng/trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng/trừ theo từng cột (theo cột dọc).

* Quy tắc nhân đơn thức với đơn thức

Muốn nhân đơn thức A với đơn thức B, ta làm như sau:

- Nhân hệ số của đơn thức A với hệ số của đơn thức B.

- Nhân luỹ thừa của biến trong A với luỹ thừa của biến trong B.

- Nhân các kết quả vừa tìm được với nhau.

Tổng quát: \(a{x^m}.b{x^n} = ab{x^{m + n}}\) (với \(a \ne 0,b \ne 0,m,n \in \mathbb{N}\)).

* Quy tắc nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức, ta làm như sau:

- Nhân đơn thức đó với từng đơn thức của đa thức.

- Cộng các tích với nhau.

Tổng quát: \(A\left( {B + C} \right) = AB + AC\); \(A\left( {B - C} \right) = AB - AC\).

* Nhân đa thức với đa thức

Muốn nhân một đa thức với một đa thức, ta làm như sau:

- Nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia.

- Cộng các tích với nhau.

Tổng quát: \(\left( {A + B} \right)\left( {C + D} \right) = AC + AD + BC + BD\).

* Quy tắc chia đơn thức cho đơn thức

Muốn chia đơn thức A cho đơn thức B (B \( \ne \) 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến trong B, ta làm như sau:

- Chia hệ số của đơn thức A cho hệ số của đơn thức B.

- Nhân các kết quả vừa tìm được với nhau.

Tổng quát: \(\left( {a{x^m}} \right):\left( {b{x^n}} \right) = \frac{a}{b}.\left( {{x^m}:{x^n}} \right) = \frac{a}{b}{x^{m - n}}\) \(\left( {a \ne 0;b \ne 0;m,n \in \mathbb{N};m \ge n} \right)\)

* Quy tắc chia đa thức cho đơn thức:

Muốn chia đa thức P cho đơn thức Q (Q \( \ne \) 0) khi số mũ của biến ở mỗi đơn thúc của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của đa thức P cho đơn thức Q rồi cộng các thương với nhau.

Tổng quát: \(\left( {A + B} \right):C = A:C + B:C\); \(\left( {A - B} \right):C = A:C - B:C\).

* Quy tắc chia đa thức một biến đã sắp xếp

Để chia một đa thức cho một đa thức khác không (đa thức đã thu gọn, sắp xếp đa thức một biến theo luỹ thừa giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia:

Bước 1.

- Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.

- Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.

- Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.

Bước 2.

Tiếp tục quá trình trên cho đến khi nhận được đa thức 0 hoặc đa thức có bậc nhỏ hơn đa thức chia.

Chú ý: Người ta chứng minh được rằng: đối với hai đa thức của cùng một biến tuỳ ý A và B, \(B \ne 0\) tồn tại duy nhất Q và R sao cho \(A = B.Q + R\), với \(R = 0\) hoặc bậc của \(R\) nhỏ hơn bậc của B.

+ Với \(R = 0\), ta nói A chia hết cho B.

+ Với \(R \ne 0\), ta nói A không chia hết cho B (phép chia có dư).

Bài tập

Bài 1: Cho hai đa thức \(P\left( x \right) =  - 5{x^4} + 2{x^2} - 5\); \(Q\left( x \right) = 5{x^4} - {x^2} + 10\). Tính \(P\left( x \right) + Q\left( x \right)\).

A. \(10{x^4} + {x^2} + 10\).

B. \(10{x^4} - 3{x^2} + 15\).

C. \({x^2} + 10\).

D. \({x^2} + 5\).

Bài 2: Biết \(M\left( x \right) = 5{x^2} + 4x\) và \(N\left( x \right) = 2x + 3\). Các hệ số của \(M\left( x \right) - N\left( x \right)\) lần lượt theo luỹ thừa tăng dần của biến là:

A. -3; 2; 5.

B. 5; 6; 3.

C. 3; 6; 5.

D. 5; 2; 3.

Bài 3: Tích của hai đơn thức \(7{x^2}\) và 3x là

A. \( - 12{x^3}\).

B. 21\({x^3}\).

C. \(12{x^2}\).

D. \(8{x^3}\).

Bài 4: Kết quả của phép nhân (x + 5) . (-x – 3) là:

A. x² + 2x + 15.

B. -x² – 8x – 15.

C. -x² – 15.

D. –x² + 2x – 15.

Bài 5: Tìm giá trị của \(a\) biết \(\left( {x + 1} \right)\left( {x - 2} \right) = {x^2} + ax - 2\)

A. \( - 1\).

B. \(1\).

C. \(2\).

D. \( - 2\).

Bài 6: Tìm kết quả của phép chia 8x⁴ - 2x³ cho 4x²

A. 2x².

B. 4x⁵.

C. 2x² - 0,5.x.

D. 2x² + 1.

Bài 7: Phép chia 2x⁴ – x³ + 2x – 1 cho x² – x + 1 có thương là:

A. 0,5. x² + 2x – 1.

B. - 2x² + 2x – 1.

C. 2x² + x – 1.

D. 2x² + x + 1.

Bài 8: Cho 3 đa thức:

A(x) = 6x² – 3x + x³ – 4x² – 5

B(x) = -2x² – 3x + 7 +2x² + x³

\(C(x) = 6{x^2} - 3x + 4 - 2{x^3} - 2x\)

a) Tính A(x)  + B(x).

b) Tính  A(x) – 3. B(x).

c) Tính A(x) + B(x) – C(x).

Bài 9: Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)

a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến.

b) Tính \(A\left( x \right) - B\left( x \right)\).

Bài 10: Cho các đa thức:

\(A\left( x \right) = 2{x^4} - 5{x^3} + 7x - 5 + 4{x^3} + 3{x^2} + 2x + 3\)

\(B\left( x \right) = 5{x^4} - 3{x^3} + 5x - 3{x^4} - 2{x^3} + 9 - 6x\)

\(C\left( x \right) = {x^4} + 4{x^2} + 5\)

a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),B\left( x \right)\) theo lũy thừa giảm dần của biến.

b) Tính \(A\left( x \right) + B\left( x \right);A\left( x \right) - B\left( x \right)\).

c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.

Bài 11: Cho \(A\left( x \right) = 4{x^2} + 4x + 1\).

a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.

b) Tính \(A\left( x \right):\left( {2x + 1} \right)\).

Bài 12: Cho hai đa thức:

\(A\left( x \right) = 9{x^4} + 2{x^2} - x + 6\);

\(B\left( x \right) = - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}\).

a) Thu gọn và sắp xếp đa thức \(B\left( x \right)\) theo luỹ thừa giảm dần của biến.

b) Chứng tỏ \(x = 9\) là nghiệm của đa thức \(P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}\).

--------Hết--------

Lời giải chi tiết:

Bài 1: Cho hai đa thức \(P\left( x \right) =  - 5{x^4} + 2{x^2} - 5\); \(Q\left( x \right) = 5{x^4} - {x^2} + 10\). Tính \(P\left( x \right) + Q\left( x \right)\).

A. \(10{x^4} + {x^2} + 10\).

B. \(10{x^4} - 3{x^2} + 15\).

C. \({x^2} + 10\).

D. \({x^2} + 5\).

Phương pháp

Để cộng, trừ đa thức một biến, ta có thể thực hiện 1 trong 2 cách sau:

Cách 1. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc (theo hàng ngang)

Cách 2. Sắp xếp các hạng tử của các đa thức theo luỹ thừa giảm (tăng) của biến rồi đặt tính cộng/trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng/trừ theo từng cột (theo cột dọc).

Lời giải

\(\begin{array}{l}P\left( x \right) + Q\left( x \right)\\ = \left( { - 5{x^4} + 2{x^2} - 5} \right) + \left( {5{x^4} - {x^2} + 10} \right)\\ =  - 5{x^4} + 2{x^2} - 5 + 5{x^4} - {x^2} + 10\\ = \left( { - 5{x^4} + 5{x^4}} \right) + \left( {2{x^2} - {x^2}} \right) + \left( { - 5 + 10} \right)\\ = {x^2} + 5\end{array}\)

Đáp án: D

Bài 2: Biết \(M\left( x \right) = 5{x^2} + 4x\) và \(N\left( x \right) = 2x + 3\). Các hệ số của \(M\left( x \right) - N\left( x \right)\) lần lượt theo luỹ thừa tăng dần của biến là:

A. -3; 2; 5.

B. 5; 6; 3.

C. 3; 6; 5.

D. 5; 2; 3.

Phương pháp

Để cộng, trừ đa thức một biến, ta có thể thực hiện 1 trong 2 cách sau:

Cách 1. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc (theo hàng ngang)

Cách 2. Sắp xếp các hạng tử của các đa thức theo luỹ thừa giảm (tăng) của biến rồi đặt tính cộng/trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng/trừ theo từng cột (theo cột dọc).

Lời giải

\(\begin{array}{l}M\left( x \right) = P\left( x \right) + Q\left( x \right)\\ = \left( {5{x^2} + 4x} \right) + \left( {2x + 3} \right)\\ =  - 3 + \left( {4x - 2x} \right) + 5{x^2}\\ =  - 3 + 2x + 5{x^2}\end{array}\).

Do đó các hệ số của \(M\left( x \right) - N\left( x \right)\) lần lượt theo luỹ thừa tăng dần của biến là: -3; 2; 5.

Đáp án: A

Bài 3: Tích của hai đơn thức \(7{x^2}\) và 3x là

A. \( - 12{x^3}\).

B. 21\({x^3}\).

C. \(12{x^2}\).

D. \(8{x^3}\).

Phương pháp

Để nhân hai đơn thức ta nhân hay hệ số với nhau và nhân hai lũy thừa của biến với nhau.

Lời giải

Ta có: \(7{x^2}.3x = 21{x^3}\).

Đáp án: B

Bài 4: Kết quả của phép nhân (x + 5) . (-x – 3) là:

A. x² + 2x + 15.

B. -x² – 8x – 15.

C. -x² – 15.

D. –x² + 2x – 15.

Phương pháp

Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Cách 2: Đặt tính nhân:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trng một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.

Lời giải

Ta có:

(x + 5) . (-x – 3)

= x . (-x) + x . (-3) + 5 . (-x) + 5 . (-3)

= -x² – 3x – 5x – 15

= -x² – 8x – 15

Đáp án: B

Bài 5: Tìm giá trị của \(a\) biết \(\left( {x + 1} \right)\left( {x - 2} \right) = {x^2} + ax - 2\)

A. \( - 1\).

B. \(1\).

C. \(2\).

D. \( - 2\).

Phương pháp

Bước 1: Nhân đa thức với đa thức

Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Cách 2: Đặt tính nhân:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trng một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.

Bước 2: Tìm a

Lời giải

Ta có: \(\left( {x + 1} \right)\left( {x - 2} \right)\)

\( = x\left( {x - 2} \right) + x - 2\)

\( = {x^2} - 2x + x - 2\)

\( = {x^2} - x - 2\)

Lại có: \(\left( {x + 1} \right)\left( {x - 2} \right) = {x^2} + ax - 2\)

\(\begin{array}{*{20}{l}}{{x^2} - x - 2 = {x^2} + ax - 2}\\{a = - 1.}\end{array}\)

Đáp án: A

Bài 6: Tìm kết quả của phép chia 8x⁴ - 2x³ cho 4x²

A. 2x².

B. 4x⁵.

C. 2x² - 0,5.x.

D. 2x² + 1.

Phương pháp

Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.

Lời giải

Ta có:

(8x⁴ - 2x³) : 4x² = 8x⁴ : 4x² - 2x³ : 4x² = 2x² – 0,5.x

Đáp án: C

Bài 7: Phép chia 2x⁴ – x³ + 2x – 1 cho x² – x + 1 có thương là:

A. 0,5. x² + 2x – 1.

B. - 2x² + 2x – 1.

C. 2x² + x – 1.

D. 2x² + x + 1.

Phương pháp

Muốn chia đa thức A cho đa thức B, ta làm như sau:

Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.

Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B

Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3

Bước 5: Làm tương tự như trên

Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.

Lời giải

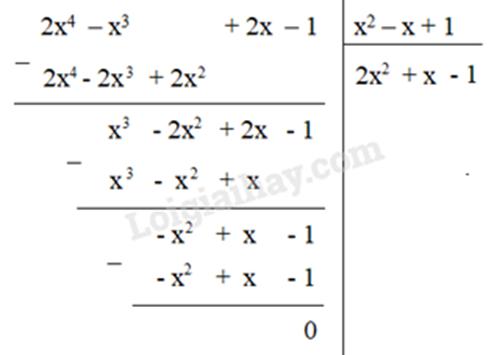
Đáp án: C

Bài 8: Cho 3 đa thức:

A(x) = 6x² – 3x + x³ – 4x² – 5

B(x) = -2x² – 3x + 7 +2x² + x³

\(C(x) = 6{x^2} - 3x + 4 - 2{x^3} - 2x\)

a) Tính A(x)  + B(x).

b) Tính  A(x) – 3. B(x).

c) Tính A(x) + B(x) – C(x).

Phương pháp

a) Bước 1: Thu gọn từng đa thức

Bước 2:

Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.

Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.

b) Bước 1: Thu gọn từng đa thức

Bước 2:

Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.

Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.

c) Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.

Cách 2: Đặt tính cộng, trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng, trừ theo từng cột.

Ta có:

Lời giải

a) Ta có:

A(x) = 6x² – 3x + x³ – 4x² – 5 = x³ + (6x² – 4x²) – 3x – 5 = x³ + 2x² – 3x – 5

B(x) = -2x² – 3x + 7 +2x² + x³ = x³ + (-2x² + 2x²) – 3x + 7 = x³ – 3x + 7

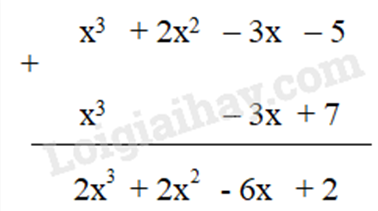
b) Ta có:

A(x) = 6x² – 3x + x³ – 4x² – 5 = x³ + (6x² – 4x²) – 3x – 5 = x³ + 2x² – 3x – 5

B(x) = -2x² – 3x + 7 +2x² + x³ = x³ + (-2x² + 2x²) – 3x + 7 = x³ – 3x + 7 nên 3. B(x) = 3.(x³ – 3x + 7) = 3x³ – 9x + 21

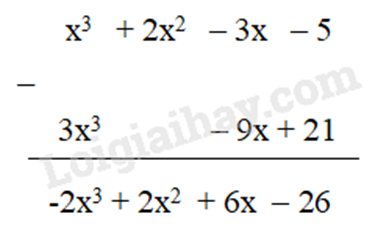
c) A(x)  = 6x² – 3x + x³ – 4x² – 5 = x³ + (6x² – 4x²) – 3x – 5 = x³ + 2x² – 3x – 5

B(x) = -2x² – 3x + 7 +2x² + x³ = x³ + (-2x² + 2x²) – 3x + 7 = x³ – 3x + 7

\(C(x) = 6{x^2} - 3x + 4 - 2{x^3} - 2x\) = -2x³ + 6x² + (-3x – 2x) + 4 = -2x³ + 6x² – 5x + 4

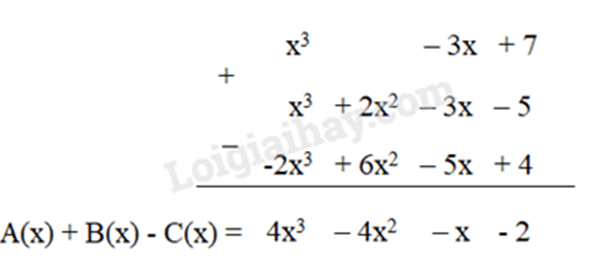
Bài 9: Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)

a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến.

b) Tính \(A\left( x \right) - B\left( x \right)\).

Phương pháp

Thực hiện tính toán với đa thức một biến.

Lời giải

a) \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\)

\(\begin{array}{*{20}{l}}{ = 5{x^4} + \left( { - 7{x^2} - 6{x^2}} \right) + \left( { - 3x + 11x} \right) - 30}\\{ = 5{x^4} - 13{x^2} + 8x - 30}\end{array}\)

\(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)

\(\begin{array}{*{20}{l}}{ = 13{x^4} + \left( { - 11{x^3} + 20{x^3}} \right) + \left( {5x - 34x} \right) + \left( { - 10 - 2} \right)}\\{ = 13{x^4} + 9{x^3} - 29x - 12}\end{array}\)

b) \(A\left( x \right) - B\left( x \right) = \left( {5{x^4} - 13{x^2} + 8x - 30} \right) - \left( {13{x^4} + 9{x^3} - 29x - 12} \right)\)

\(\begin{array}{*{20}{l}}{ = 5{x^4} - 13{x^2} + 8x - 30 - 13{x^4} - 9{x^3} + 29x + 12}\\{ = \left( {5{x^4} - 13{x^4}} \right) - 9{x^3} - 13{x^2} + \left( {8x + 29x} \right) + \left( { - 30 + 12} \right)}\\{ =  - 8{x^4} - 9{x^3} - 13{x^2} + 37x - 18}\end{array}\)

Bài 10: Cho các đa thức:

\(A\left( x \right) = 2{x^4} - 5{x^3} + 7x - 5 + 4{x^3} + 3{x^2} + 2x + 3\)

\(B\left( x \right) = 5{x^4} - 3{x^3} + 5x - 3{x^4} - 2{x^3} + 9 - 6x\)

\(C\left( x \right) = {x^4} + 4{x^2} + 5\)

a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),B\left( x \right)\) theo lũy thừa giảm dần của biến.

b) Tính \(A\left( x \right) + B\left( x \right);A\left( x \right) - B\left( x \right)\).

c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.

Phương pháp

a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),B\left( x \right)\) theo lũy thừa giảm dần của biến.

b) Tính \(A\left( x \right) + B\left( x \right);A\left( x \right) - B\left( x \right)\).

c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.

Lời giải

a) Thu gọn:

\(\begin{array}{*{20}{l}}{A\left( x \right) = 2{x^4} - 5{x^3} + 7x - 5 + 4{x^3} + 3{x^2} + 2x + 3}\\{A\left( x \right) = 2{x^4} + \left( { - 5{x^3} + 4{x^3}} \right) + 3{x^2} + \left( {7x + 2x} \right) - 5 + 3}\\{A\left( x \right) = 2{x^4} - {x^3} + 3{x^2} + 9x - 2}\end{array}\)

\(\begin{array}{*{20}{l}}{B\left( x \right) = 5{x^4} - 3{x^3} + 5x - 3{x^4} - 2{x^3} + 9 - 6x}\\{B\left( x \right) = \left( {5{x^4} - 3{x^4}} \right) + \left( { - 3{x^3} - 2{x^3}} \right) + \left( {5x - 6x} \right) + 9}\\{B\left( x \right) = 2{x^4} - 5{x^3} - x + 9}\end{array}\)

b) Tính \(A\left( x \right) + B\left( x \right);A\left( x \right) - B\left( x \right)\).

\(\begin{array}{*{20}{l}}{ + )A\left( x \right) + B\left( x \right) = \left( {2{x^4} - {x^3} + 3{x^2} + 9x - 2} \right) + \left( {2{x^4} - 5{x^3} - x + 9} \right)}\\{ = \left( {2{x^4} + 2{x^4}} \right) + \left( { - {x^3} - 5{x^3}} \right) + 3{x^2} + \left( {9x - x} \right) + \left( { - 2 + 9} \right)}\\{ = 4{x^4} - 6{x^3} + 3{x^2} + 8x + 7}\end{array}\)

\(\begin{array}{*{20}{l}}{ + )A\left( x \right) - B\left( x \right) = \left( {2{x^4} - {x^3} + 3{x^2} + 9x - 2} \right) - \left( {2{x^4} - 5{x^3} - x + 9} \right)}\\{ = \left( {2{x^4} - {x^3} + 3{x^2} + 9x - 2} \right) - 2{x^4} + 5{x^3} + x - 9}\\{ = \left( {2{x^4} - 2{x^4}} \right) + \left( { - {x^3} + 5{x^3}} \right) + 3{x^2} + \left( {9x + x} \right) + \left( { - 2 - 9} \right)}\\{ = 4{x^3} + 3{x^2} + 10x - 11}\end{array}\)

c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.

Ta có: \(C\left( x \right) = {x^4} + 4{x^2} + 5\).

Vì \({x^4} > 0,\forall x\) và \({x^2} > 0,\forall x\) nên \(C\left( x \right) > 0,\forall x.\)

Suy ra không có giá trị nào của \(x\) làm cho \(C\left( x \right) = 0\).

Vậy \(C\left( x \right)\) là đa thức không có nghiệm.

Bài 11: Cho \(A\left( x \right) = 4{x^2} + 4x + 1\).

a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.

b) Tính \(A\left( x \right):\left( {2x + 1} \right)\).

Phương pháp

a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.

b) Áp dụng quy tắc chia đa thức để tính.

Lời giải

a) Bậc của đa thức là 2.

Hạng tử tự do là 1.

Hạng tử cao nhất của đa thức là 4.

b) Ta có: \(A\left( x \right):\left( {2x + 1} \right) = \left( {4{x^2} + 4x + 1} \right):\left( {2x + 1} \right)\)

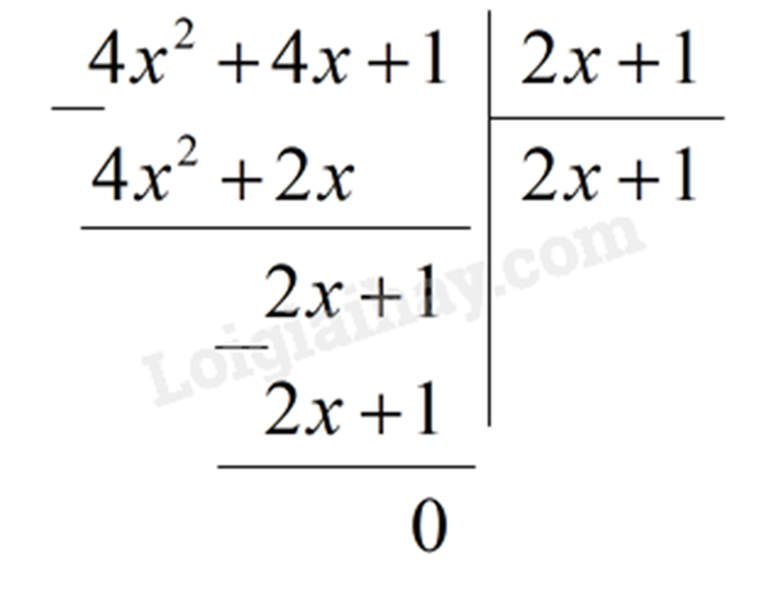
Vậy \(A\left( x \right):\left( {2x + 1} \right) = 2x + 1\)

Bài 12: Cho hai đa thức:

\(A\left( x \right) = 9{x^4} + 2{x^2} - x + 6\);

\(B\left( x \right) = - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}\).

a) Thu gọn và sắp xếp đa thức \(B\left( x \right)\) theo luỹ thừa giảm dần của biến.

b) Chứng tỏ \(x = 9\) là nghiệm của đa thức \(P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}\).

Phương pháp

a) Bước 1: Cộng, trừ các đơn thức cùng bậc để thu được đa thức thu gọn không chứa hai đơn thức nào cùng bậc

Bước 2: Sắp xếp đa thức trên theo lũy thừa giảm của biến.

b) Tìm đa thức P(x).

Thay \(x = 9\) vào \(P\left( x \right)\), nếu \(P\left( 9 \right) = 0\) thì \(x = 9\) là nghiệm của \(P\left( x \right)\).

Lời giải

a) Ta có:

\(\begin{array}{*{20}{l}}{B\left( x \right) = - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}}\\{B\left( x \right) = - 8{x^4} + \left( {4{x^3} - 5{x^3}} \right) - 2{x^2} + 3}\\{B\left( x \right) = - 8{x^4} - {x^3} - 2{x^2} + 3}\end{array}\)

b) Ta có:

\(\begin{array}{*{20}{l}}{P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}}\\{P\left( x \right) = \left( {9{x^4} + 2{x^2} - x + 6} \right) + \left( { - 8{x^4} - {x^3} - 2{x^2} + 3} \right) - {x^4} + {x^3}}\\{P\left( x \right) = 9{x^4} + 2{x^2} - x + 6 - 8{x^4} - {x^3} - 2{x^2} + 3 - {x^4} + {x^3}}\\{P\left( x \right) = \left( {9{x^4} - 8{x^4} - {x^4}} \right) + \left( { - {x^3} + {x^3}} \right) + \left( {2{x^2} - 2{x^2}} \right) - x + \left( {6 + 3} \right)}\\{P\left( x \right) = - x + 9}\end{array}\)

Ta có: \(P\left( 9 \right) = - 9 + 9 = 0\) nên \(x = 9\) là nghiệm của \(P\left( x \right)\).