Đề ôn hè Toán 7 lên 8 - Đề 10

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Số đối của \(\frac{3}{4}\) là?

A. \( - \frac{3}{4}\).

B. \(\frac{4}{3}\).

C. \(\frac{{ - 3}}{{ - 4}}\).

D. \( - \frac{4}{3}\).

Câu 2: Cho \(a{\mkern 1mu} {\rm{//}}{\mkern 1mu} b\), số đo góc \(x\) trên hình vẽ bằng:

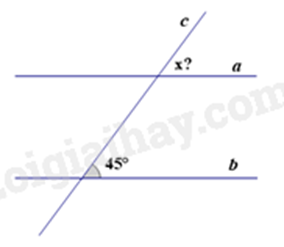
A. \(135^\circ \).

B. \(90^\circ \).

C. \(45^\circ \).

D. \(0^\circ \).

Câu 3: Trong các hình vẽ dưới đây, hình vẽ nào cho biết Ot là tia phân giác của góc xOy?

A.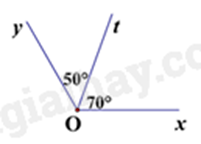 

B.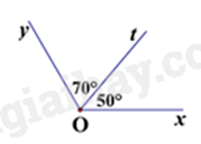 

C.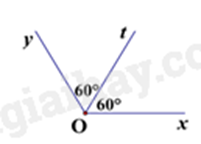 

D.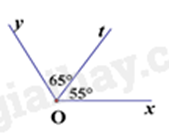 

Câu 4: Hình vẽ nào dưới đây cho biết đường thẳng d là đường trung trực của đoạn thẳng AB?

A.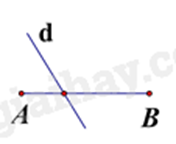 

B.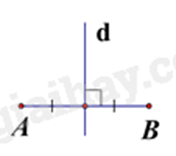 

C.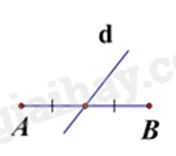 

D.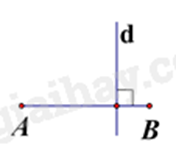 

Câu 5: Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?

A. AB = BC.

B. AB = AC.

C. \(\widehat B = \widehat C\).

D. \(\widehat B = \frac{{{{180}^0} - \widehat A}}{2}\).

Câu 6: Thứ tự nào sau đây đúng?

A. \( - \sqrt 3  < 0 < \sqrt 3 \).

B. \( - \sqrt 3  < \sqrt 3  < 0\).

C. \(0 <  - \sqrt 3  < \sqrt 3 \).

D. \(0 < \sqrt 3  <  - \sqrt 3 \).

Câu 7: Bậc của đa thức \(P =  - 5{x^7} + 4{x^8} - 4x + 6\) là

A. 8.

B. 7.

C. 1.

D. 0.

Câu 8: Bộ ba độ dài đoạn thẳng nào sau đây tạo thành độ dài ba cạnh của một tam giác? 

A. 5cm; 4cm; 1cm.

B. 1cm; 4cm; 10cm.

C. 5cm; 2cm; 2cm.

D. 3cm; 4cm; 5cm.

Câu 9: Cho biết 3 máy cày (các máy cày có cùng năng suất) cày xong một cánh đồng hết 30 giờ. Vậy 5 máy cày như thế cày xong cánh đồng đó hết

A. 25 giờ.

B. 16 giờ.

C. 18 giờ.

D. 20 giờ.

Câu 10: “Khi gieo đồng xu thì được mặt sấp” là:

A. Biến cố ngẫu nhiên.

B. Biến cố chắc chắn.

C. Biến cố không thể.

D. Không phải là biến cố.

Câu 11: Lớp 7A có 20 bạn nam và 20 bạn nữ. giáo viên gọi ngẫu nhiên 1 bạn lên bảng để kiểm tra bài tập. Xác suất để giáo viên gọi được bạn nữ là:

A. \(\frac{1}{6}\).

 B. 1.

 C. \(\frac{1}{3}\).

D. \(\frac{1}{2}\).

Câu 12: Cho \(\Delta ABC\) nếu \(O\) là điểm cách đều ba đỉnh của tam giác. Khi đó \(O\) là giao điểm của

A. ba đường cao.

B. ba đường trung tuyến.

C. ba đường trung trực.

D. ba đường phân giác.

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm)

1. Thực hiện các phép tính sau (tính nhanh nếu có thể):

a) \({\left( { - \frac{1}{2}} \right)^2}.\frac{4}{{11}} + \frac{7}{{11}}.{\left( { - \frac{1}{2}} \right)^2}\)

b) \({\left( { - \frac{1}{3}} \right)^2} + 2:\left| { - \frac{1}{2}} \right| - \sqrt {16}  - {2024^0}\)

2. Tìm \(x\), biết: \(\frac{6}{5} - \left| {x - \frac{1}{2}} \right| = \frac{3}{4}\).

Bài 2. (1 điểm) Biểu đồ sau thể hiện loại kem bán được trong một ngày của một cửa hàng.

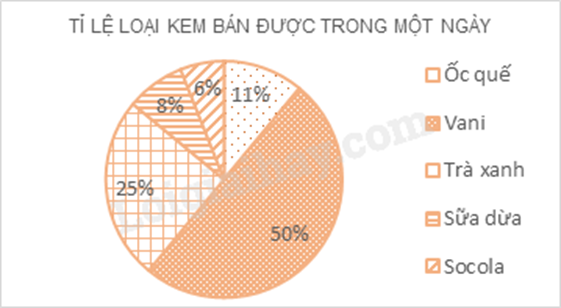
a) Em hãy lập bảng thống kê tỉ lệ các loại kem bán được trong một ngày của cửa hàng.

b) Biết một ngày của hàng đó bán được 200 cây kem. Em hãy tính số kem Vani đã bán được trong một ngày.

Bài 3. (1 điểm) Cho hai đa thức:

\(M\left( x \right) =  - 5{x^4} + 3{x^5} + x\left( {{x^2} + 5} \right) + 14{x^4} - 6{x^5} - {x^3} + x - 1\); \(N\left( x \right) = {x^4}\left( {x - 5} \right) - 3{x^3} + 3x + 2{x^5} - 4{x^4} + 3{x^3} - 5\).

a) Tính \(H\left( x \right) = M\left( x \right) + N\left( x \right)\).

b) Tìm nghiệm của đa thức \(H\left( x \right)\).

Bài 4. (1 điểm) Học sinh của ba lớp 7 cần phải trồng chăm sóc một số cây xanh. Lớp 7A có 32 học sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết số cây tỉ lệ với số học sinh và tổng số cây của lớp 7A và 7B nhiều hơn lớp 7C là 6 cây.

Bài 5. (2,5 điểm)

1. Một thùng dự trữ dầu trong nhà máy có dạng hình hộp chữ nhật có chiều dài 5 m, chiều rộng 4 m và chiều cao 3 m.

a) Tính thể tích của thùng.

b) Người thợ phải tốn bao nhiêu tiền mua sơn để đủ sơn các mặt xung quanh của chiếc thùng? Biết rằng mỗi kg sơn sơn được 9m² và giá tiền 1kg sơn có giá 250 000 đồng.

2. Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Gọi M là trung điểm của CD, đường thẳng qua D và song song với BC cắt đường thẳng BM tại E.

a) Chứng minh rằng ∆CBD là tam giác cân.

b) Gọi G là giao điểm của AE và DM. Chứng minh rằng \(BC = 6.GM\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Số đối của \(\frac{3}{4}\) là?

A. \( - \frac{3}{4}\).

B. \(\frac{4}{3}\).

C. \(\frac{{ - 3}}{{ - 4}}\).

D. \( - \frac{4}{3}\).

Phương pháp

Số đối của a là – a.

Lời giải

Số đối của \(\frac{3}{4}\) là \( - \frac{3}{4}\).

Đáp án: A

Câu 2: Cho \(a{\mkern 1mu} {\rm{//}}{\mkern 1mu} b\), số đo góc \(x\) trên hình vẽ bằng:

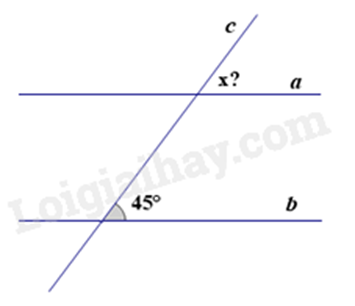
A. \(135^\circ \).

B. \(90^\circ \).

C. \(45^\circ \).

D. \(0^\circ \).

Phương pháp

Hai đường thẳng song song thì hai góc đồng vị bằng nhau.

Lời giải

Số đo góc x là \(45^\circ \) (hai góc đồng vị bằng nhau do a // b).

Đáp án: C

Câu 3: Trong các hình vẽ dưới đây, hình vẽ nào cho biết Ot là tia phân giác của góc xOy?

A.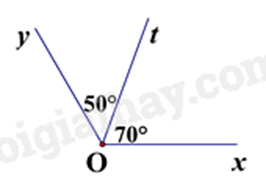 

B.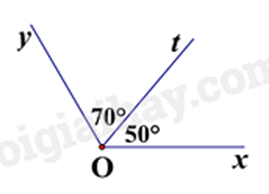 

C.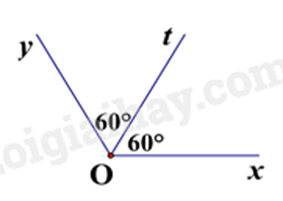 

D.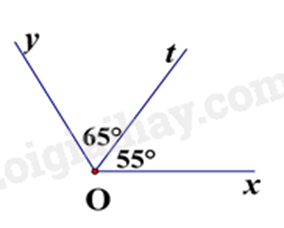 

Phương pháp

Tia phân giác của một góc nằm trong góc đó và chia góc thành hai phần bằng nhau.

Lời giải

Hình C có Ot là tia phân giác của góc xOy do Ot nằm giữa Ox và Oy và \(\widehat {xOt} = \widehat {tOy} = 60^\circ \).

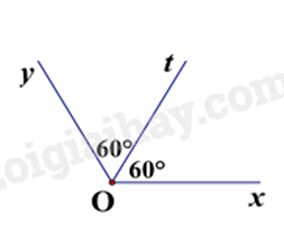
Đáp án: C

Câu 4: Hình vẽ nào dưới đây cho biết đường thẳng d là đường trung trực của đoạn thẳng AB?

A.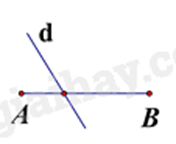 

B.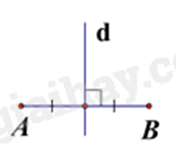 

C.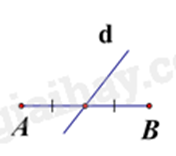 

D.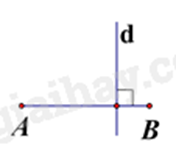 

Phương pháp

Đường trung trực của đoạn thẳng là đường thẳng vuông góc với đường thẳng đó tại trung điểm.

Lời giải

Hình B, đường thẳng d là đường trung trực của đoạn thẳng AB.

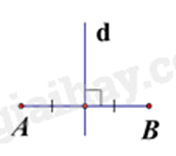
Đáp án: B

Câu 5: Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?

A. AB = BC.

B. AB = AC.

C. \(\widehat B = \widehat C\).

D. \(\widehat B = \frac{{{{180}^0} - \widehat A}}{2}\).

Phương pháp

Tam giác cân có hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau.

Lời giải

Vì tam giác ABC cân tại A nên AB = AC, \(\widehat B = \widehat C\).

Vì tổng ba góc trong tam giác bằng \(180^\circ \) nên \(\widehat A + \widehat B + \widehat C = 180^\circ \), suy ra \(\widehat B + \widehat C = 180^\circ  - \widehat A\).

Mà \(\widehat B = \widehat C\) nên \(\widehat B = \widehat C = \frac{{180^\circ  - \widehat A}}{2}\).

Vậy B, C, D đúng, A sai.

Đáp án: A

Câu 6: Thứ tự nào sau đây đúng?

A. \( - \sqrt 3  < 0 < \sqrt 3 \).

B. \( - \sqrt 3  < \sqrt 3  < 0\).

C. \(0 <  - \sqrt 3  < \sqrt 3 \).

D. \(0 < \sqrt 3  <  - \sqrt 3 \).

Phương pháp

So sánh số thực âm, dương và số 0.

Lời giải

Vì \( - \sqrt 3 \) là số thực âm, \(\sqrt 3 \) là số thực dương nên \( - \sqrt 3  < 0 < \sqrt 3 \).

Đáp án: A

Câu 7: Bậc của đa thức \(P =  - 5{x^7} + 4{x^8} - 4x + 6\) là

A. 8.

B. 7.

C. 1.

D. 0.

Phương pháp

Bậc của đa thức là bậc của hạng tử có số mũ lớn nhất.

Lời giải

Bậc của đa thức \(P =  - 5{x^7} + 4{x^8} - 4x + 6 = 4{x^8} - 5{x^7} - 4x + 6\) là 8.

Đáp án: A

Câu 8: Bộ ba độ dài đoạn thẳng nào sau đây tạo thành độ dài ba cạnh của một tam giác? 

A. 5cm; 4cm; 1cm.

B. 1cm; 4cm; 10cm.

C. 5cm; 2cm; 2cm.

D. 3cm; 4cm; 5cm.

Phương pháp

Sử dụng bất đẳng thức tam giác để kiểm tra.

Lời giải

Ta có: 4 + 1 = 5 không thoả mãn bất đẳng thức tam giác nên 5cm; 4cm; 1cm không phải ba cạnh của một tam giác.

Ta có: 1 + 4 = 5 < 10 không thoả mãn bất đẳng thức tam giác nên 1cm; 4cm; 10cm không phải ba cạnh của một tam giác.

Ta có: 2 + 2 = 4 < 5 không thoả mãn bất đẳng thức tam giác nên 5cm; 2cm; 2cm không phải ba cạnh của một tam giác.

Ta có: 3 + 4 = 7 > 5 nên 3cm; 4cm; 5cm là ba cạnh của tam giác.

Đáp án: D

Câu 9: Cho biết 3 máy cày (các máy cày có cùng năng suất) cày xong một cánh đồng hết 30 giờ. Vậy 5 máy cày như thế cày xong cánh đồng đó hết

A. 25 giờ.

B. 16 giờ.

C. 18 giờ.

D. 20 giờ.

Phương pháp

Sử dụng kiến thức về đại lượng tỉ lệ nghịch để tính.

Lời giải

Gọi thời gian 5 máy cày như thế cày xong cánh đồng đó là \(x\) (giờ)

Vì máy cày và số giờ là hai đại lượng tỉ lệ nghịch nên ta có:

\(5x = 3.30\), suy ra \(x = \frac{{3.30}}{5} = 18\) (giờ).

Vậy 5 máy cày như thế cày xong cánh đồng đó hết 18 giờ.

Đáp án: C

Câu 10: “Khi gieo đồng xu thì được mặt sấp” là:

A. Biến cố ngẫu nhiên.

B. Biến cố chắc chắn.

C. Biến cố không thể.

D. Không phải là biến cố.

Phương pháp

Các hiện tượng, sự kiện trong tự nhiên, cuộc sống được gọi chung là biến cố.

- Biến cố chắc chắn là biến cố biết trước được luôn xảy ra.

- Biến cố không thể là biến cố biết trước được không bao giờ xảy ra.

- Biến cố ngẫu nhiên là biến cố không thể biết trước được có xảy ra hay không.

Lời giải

Khi gieo đồng xu thì mặt xuất hiện có thể là mặt sấp hoặc mặt ngửa.

Vậy biến cố “Khi gieo đồng xu thì được mặt sấp” là biến cố ngẫu nhiên.

Đáp án: A

Câu 11: Lớp 7A có 20 bạn nam và 20 bạn nữ. giáo viên gọi ngẫu nhiên 1 bạn lên bảng để kiểm tra bài tập. Xác suất để giáo viên gọi được bạn nữ là:

A. \(\frac{1}{6}\).

 B. 1.

 C. \(\frac{1}{3}\).

D. \(\frac{1}{2}\).

Phương pháp

Dựa vào kiến thức về hai biến cố đồng khả năng.

Trong một trò chơi hay thí nghiệm, nếu có k biến cố đồng khả năng và luôn xảy ra duy nhất một biến cố trong k biến cố này thì xác suất của mỗi biến cố đó đều bằng \(\frac{1}{k}\).

Lời giải

Xét hai biến cố sau:

A: “Bạn được gọi là bạn nữ”

B: “Bạn được gọi là bạn nam”

Hai biến cố A và B đồng khả năng vì đều có 20 khả năng cô gọi trúng bạn nam và 20 khả năng cô gọi trúng bạn nữ.

Do đó xác suất của mỗi biến cố đó là: \(\frac{1}{2}\).

Đáp án: D

Câu 12: Cho \(\Delta ABC\) nếu \(O\) là điểm cách đều ba đỉnh của tam giác. Khi đó \(O\) là giao điểm của

A. ba đường cao.

B. ba đường trung tuyến.

C. ba đường trung trực.

D. ba đường phân giác.

Phương pháp

Điểm cách đều ba đỉnh là giao điểm của ba đường trung trực.

Lời giải

O cách đều ba đỉnh của tam giác ABC nên O là giao điểm của ba đường trung trực.

Đáp án: C

Phần tự luận.

Bài 1. (1,5 điểm)

1. Thực hiện các phép tính sau (tính nhanh nếu có thể):

a) \({\left( { - \frac{1}{2}} \right)^2}.\frac{4}{{11}} + \frac{7}{{11}}.{\left( { - \frac{1}{2}} \right)^2}\)

b) \({\left( { - \frac{1}{3}} \right)^2} + 2:\left| { - \frac{1}{2}} \right| - \sqrt {16}  - {2024^0}\)

2. Tìm \(x\), biết: \(\frac{6}{5} - \left| {x - \frac{1}{2}} \right| = \frac{3}{4}\).

Phương pháp

1. Sử dụng quy tắc cộng, trừ, nhân, chia với số thực.

2. Chuyển vế.

Sử dụng kiến thức về giá trị tuyệt đối: \(\left| A \right| = B\) thì \(A = B\) hoặc \(A =  - B\).

Lời giải

1.

a) \({\left( { - \frac{1}{2}} \right)^2}.\frac{4}{{11}} + \frac{7}{{11}}.{\left( { - \frac{1}{2}} \right)^2} = \frac{1}{4}.\frac{4}{{11}} + \frac{7}{{11}}.\frac{1}{4} = \frac{1}{4}\left( {\frac{4}{{11}} + \frac{7}{{11}}} \right) = \frac{1}{4}.1 = \frac{1}{4}\)

b)\({\left( { - \frac{1}{3}} \right)^2} + 2:\left| { - \frac{1}{2}} \right| - \sqrt {16}  - {2024^0} = \frac{1}{9} + 4 - 4 - 1 = \frac{1}{9} - 1 = \frac{1}{9} - \frac{9}{9} =  - \frac{8}{9}\)

2.

\(\begin{array}{l}\frac{6}{5} - \left| {x - \frac{1}{2}} \right| = \frac{3}{4}\\\left| {x - \frac{1}{2}} \right| = \frac{6}{5} - \frac{3}{4}\\\left| {x - \frac{1}{2}} \right| = \frac{9}{{20}}\end{array}\)

Trường hợp 1:

 \(x - \frac{1}{2} = \frac{9}{{20}}\)

 \(\begin{array}{l}x = \frac{9}{{20}} + \frac{1}{2}\\x = \frac{{19}}{{20}}\end{array}\)

Trường hợp 2:

 \(\begin{array}{l}x - \frac{1}{2} =  - \frac{9}{{20}}\\x =  - \frac{9}{{20}} + \frac{1}{2}\\x = \frac{1}{{20}}\end{array}\)

Vậy \(x = \frac{{19}}{{20}};x = \frac{1}{{20}}\).

Bài 2. (1 điểm) Biểu đồ sau thể hiện loại kem bán được trong một ngày của một cửa hàng.

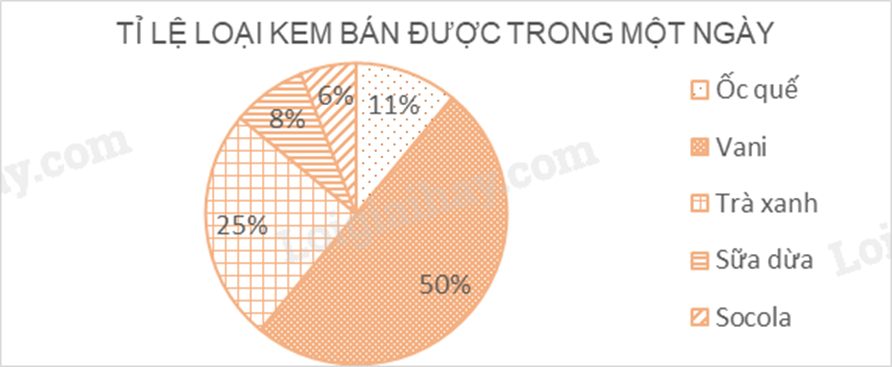
a) Em hãy lập bảng thống kê tỉ lệ các loại kem bán được trong một ngày của cửa hàng.

b) Biết một ngày của hàng đó bán được 200 cây kem. Em hãy tính số kem Vani đã bán được trong một ngày.

Phương pháp

a) Quan sát biểu đồ hình quạt tròn, xác định tỉ lệ % tương ứng với từng loại kem.

b) Tính số kem Vani khi biết tỉ lệ phần trăm tương ứng.

Lời giải

a) Bảng thống kê biểu diễn tỉ lệ phần trăm các loại kem bán được trong một ngày của cửa hàng.

b) Số kem Vani đã bán được trong một ngày là: 50%. 200 = 100 (cây kem)

Bài 3. (1 điểm) Cho hai đa thức:

\(M\left( x \right) =  - 5{x^4} + 3{x^5} + x\left( {{x^2} + 5} \right) + 14{x^4} - 6{x^5} - {x^3} + x - 1\); \(N\left( x \right) = {x^4}\left( {x - 5} \right) - 3{x^3} + 3x + 2{x^5} - 4{x^4} + 3{x^3} - 5\).

a) Tính \(H\left( x \right) = M\left( x \right) + N\left( x \right)\).

b) Tìm nghiệm của đa thức \(H\left( x \right)\).

Phương pháp

a) Thu gọn \(M\left( x \right),N\left( x \right)\)

Thực hiện theo quy tắc cộng hai đa thức để tính \(H\left( x \right)\).

b) Giải \(H\left( x \right) = 0\) để tìm nghiệm.

Lời giải

a) +) \(M\left( x \right) =  - 5{x^4} + 3{x^5} + x\left( {{x^2} + 5} \right) + 14{x^4} - 6{x^5} - {x^3} + x - 1\)

\(M\left( x \right) =  - 5{x^4} + 3{x^5} + {x^3} + 5x + 14{x^4} - 6{x^5} - {x^3} + x - 1\)

\(M\left( x \right) = \left( {3{x^5} - 6{x^5}} \right) + \left( { - 5{x^4} + 14{x^4}} \right) + \left( {{x^3} - {x^3}} \right) + \left( {5x + x} \right) - 1\)

\(M\left( x \right) =  - 3{x^5} + 9{x^4} + 6x - 1\).

+) \(N\left( x \right) = {x^4}\left( {x - 5} \right) - 3{x^3} + 3x + 2{x^5} - 4{x^4} + 3{x^3} - 5\)

\(N\left( x \right) = {x^5} - 5{x^4} - 3{x^3} + 3x + 2{x^5} - 4{x^4} + 3{x^3} - 5\)

\(N\left( x \right) = \left( {{x^5} + 2{x^5}} \right) + \left( { - 5{x^4} - 4{x^4}} \right) + \left( { - 3{x^3} + 3{x^3}} \right) + 3x - 5\)

\(N\left( x \right) = 3{x^5} - 9{x^4} + 3x - 5\).

Ta có:

\(H\left( x \right) = M\left( x \right) + N\left( x \right)\)

\(H\left( x \right) =  - 3{x^5} + 9{x^4} + 6x - 1 + 3{x^5} - 9{x^4} + 3x - 5\)

\(H\left( x \right) = \left( { - 3{x^5} + 3{x^5}} \right) + \left( {9{x^4} - 9{x^4}} \right) + \left( {6x + 3x} \right) + \left( { - 1 - 5} \right)\)

\(H\left( x \right) = 9x - 6\).

Vậy \(H\left( x \right) = 9x - 6\).

b) Ta có:

\(H\left( x \right) = 0\)

\(9x - 6 = 0\)

\(9x = 6\)

\(x = \frac{6}{9} = \frac{2}{3}\)

Vậy nghiệm của \(H\left( x \right)\) là \(\frac{2}{3}\).

Bài 4. (1 điểm) Học sinh của ba lớp 7 cần phải trồng chăm sóc một số cây xanh. Lớp 7A có 32 học sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết số cây tỉ lệ với số học sinh và tổng số cây của lớp 7A và 7B nhiều hơn lớp 7C là 6 cây.

Phương pháp

Gọi số cây cần trồng và chăm sóc của ba lớp 7A, 7B và 7C lần lượt là x, y và z (cây), x, y, z \( \in \)\(N*\)

Từ số cây của ba chi đội lần lượt tỉ lệ thuận với các số học sinh, thiết lập dãy tỉ số bằng nhau.

Từ tổng số cây của lớp 7A và 7B nhiều hơn lớp 7C là 6 cây, thiết lập mối liên hệ giữa x, y, z.

Áp dụng tính chất của dãy tỉ số bằng nhau để tìm x, y, z.

Lời giải

Gọi số cây cần trồng và chăm sóc của ba lớp 7A, 7B và 7C lần lượt là x, y và z (cây), x, y, z \( \in \)\(N*\)

Vì số cây của ba chi đội lần lượt tỉ lệ thuận với các số học sinh, nên ta có:

 \(\frac{x}{{32}} = \frac{y}{{28}} = \frac{z}{{36}}\)

Vì tổng số cây của lớp 7A và 7B nhiều hơn lớp 7C là 6 cây, nên: \(x + y - z = 6\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{{32}} = \frac{y}{{28}} = \frac{z}{{36}} = \frac{{x + y - z}}{{32 + 28 - 36}} = \frac{6}{{24}} = \frac{1}{4}\)

Suy ra \(x = 32.\frac{1}{4} = 8\) (cây);

           \(y = 28.\frac{1}{4} = 7\) (cây);

           \(z = 36.\frac{1}{4} = 9\) (cây).

Vậy số cây cần trồng và chăm sóc của ba lớp 7A, 7B và 7C lần lượt là 8 cây, 7 cây, 9 cây.

Bài 5. (2,5 điểm)

1. Một thùng dự trữ dầu trong nhà máy có dạng hình hộp chữ nhật có chiều dài 5 m, chiều rộng 4 m và chiều cao 3 m.

a) Tính thể tích của thùng.

b) Người thợ phải tốn bao nhiêu tiền mua sơn để đủ sơn các mặt xung quanh của chiếc thùng? Biết rằng mỗi kg sơn sơn được 9m² và giá tiền 1kg sơn có giá 250 000 đồng.

2. Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Gọi M là trung điểm của CD, đường thẳng qua D và song song với BC cắt đường thẳng BM tại E.

a) Chứng minh rằng ∆CBD là tam giác cân.

b) Gọi G là giao điểm của AE và DM. Chứng minh rằng \(BC = 6.GM\).

Phương pháp

1.

a) Tính thể tích thùng bằng thể tích hình hộp chữ nhật:

V = chiều dài. chiều rộng. chiều cao.

b) Tính diện tích xung quanh của chiếc thùng.

Tính số kg sơn cần dùng = diện tích xung quanh của chiếc thùng : số m² mỗi kg sơn được.

Tính chi phí cần chi trả = số kg sơn cần dùng. giá tiền 1kg.

2.

a) Chứng minh \(\Delta ABC = \Delta ADC\), suy ra CB = CD nên \(\Delta CBD\) cân tại C.

b) Chứng minh G là trọng tâm của \(\Delta BDE\). suy ra \(GM = \frac{1}{3}DM\).

Áp dụng tính chất của trọng tâm và tính chất trung điểm để chứng minh BC = 6.GM.

Lời giải

1.

a) Thể tích của thùng là: \(V = 5.4.3 = 60\left( {{m^2}} \right)\).

b) Diện tích xung quanh của thùng là:

\({S_{xq}} = 2\left( {5 + 4} \right).3 = 54\left( {{m^2}} \right)\).

Số kg sơn cần dùng là: \(54:9 = 6\left( {kg} \right)\)

Số tiền cần chi trả là: 6.250 000 = 1 500 000 (đồng).

2.

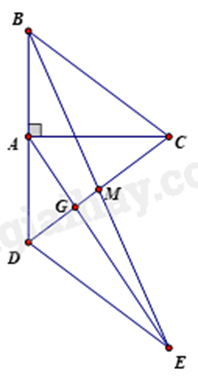
a) Xét \(\Delta ABC\) và \(\Delta ADC\) có

\(\widehat {CAB} = \widehat {CAD}\left( { = 90^\circ } \right)\)

AC chung

AB = AD (gt)

Do đó \(\Delta ABC = \Delta ADC\) (c.g.c).

Suy ra CB = CD, nên \(\Delta CBD\) cân tại C.

b) Xét \(\Delta BDE\) có:

AD = AB nên EA là đường trung tuyến của \(\Delta BDE\).

BM = ME nên DM là đường trung tuyến của \(\Delta BDE\).

Mà G là giao điểm của EA và DM

nên G là trọng tâm của \(\Delta BDE\).

Suy ra \(GM = \frac{1}{3}DM\).

Mà M là trung điểm của CD nên \(DM = \frac{1}{2}CD\).

Suy ra \(GM = \frac{1}{3}.\frac{1}{2}CD = \frac{1}{6}CD\). Do đó \(CD = 6GM\).

Mà BC = CD (cmt)

Suy ra BC = 6.GM.