Vở bài tập Toán 5 tập 2 - Kết nối tri thức

Bài 75: Ôn tập chung (tiết 4) trang 134 vở bài tập Toán 5 - Kết nối tri thức

Biểu đồ dưới đây cho biết số học sinh tham gia bốn môn Cờ vua, Bóng ném, Võ dân tộc, Bơi trong Hội khoẻ Phù Đổng của một trường tiểu học.

Lựa chọn câu để xem lời giải nhanh hơn

Bài 1

Giải Bài 1 trang 134 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống

Biểu đồ dưới đây cho biết số học sinh tham gia bốn môn Cờ vua, Bóng ném, Võ dân tộc, Bơi trong Hội khoẻ Phù Đổng của một trường tiểu học.

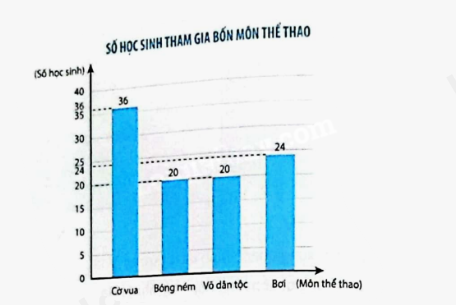
a) Hoàn thành bảng sau.

Môn	Bơi	Võ dân tộc	Bóng ném	Cờ vua
Học sinh

b) Tìm tỉ số phần trăm của số học sinh tham gia ở mỗi môn và tổng số học sinh tham gia.

Phương pháp giải:

a) Quan sát biểu đồ rồi trả lời câu hỏi

b) Tỉ số phần trăm của số học sinh tham gia ở mỗi môn và tổng số học sinh tham gia = Số học sinh tham gia ở mỗi môn : Tổng số học sinh x 100%.

Lời giải chi tiết:

Môn	Bơi	Võ dân tộc	Bóng ném	Cờ vua
Học sinh	24	20	20	36

Tỉ số phần trăm của số học sinh tham gia môn Bơi và tổng số học sinh tham gia là :

24 : 100 x 100% = 24%

Tỉ số phần trăm của số học sinh tham gia môn Võ dân tộc và tổng số học sinh tham gia là :

20 : 100 x 100% = 20%

Tỉ số phần trăm của số học sinh tham gia môn Bóng ném và tổng số học sinh tham gia là :

20 : 100 x 100% = 20%

Tỉ số phần trăm của số học sinh tham gia môn Cờ vua và tổng số học sinh tham gia là :

36 : 100 x 100% = 36%

Bài 2

Giải Bài 2 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống

Viết số thích hợp vào chỗ chấm.

Một bể cá dạng hình hộp chữ nhật có chu vi đáy là 300 cm, chiều dài hơn chiều rộng 30 cm, chiều cao bể cá là 60 cm.

a) - Chiều dài đáy bể cá là .......... cm.

- Chiều rộng đáy bể cá là .......... cm.

b) Biết mực nước ở bể cá là 42 cm.

Lượng nước trong bể chiếm ........% so với lượng nước khi đầy bể.

Phương pháp giải:

- Chiều dài = (Nửa chu vi đáy + Chênh lệch kích thước chiều dài và chiều rộng) : 2.

- Chiều rộng = Nửa chu vi đáy – Chiều dài.

- Thể tích bể cá = Chiều dài x Chiều rộng x Chiều cao.

- Thể tích nước trong bể cá = Chiều dài x Chiều rộng x Chiều cao mực nước.

- Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể = Thể tích nước trong bể cá : Thể tích bể cá x 100%.

Lời giải chi tiết:

- Chiều dài đáy bể cá là (300 : 2 + 30) : 2 = 90 cm.

- Chiều rộng đáy bể cá là 300 : 2 – 90 = 60 cm.

Thể tích bể cá là:

90 x 60 x 60 = 324 000 (cm³)

Thể tích nước trong bể cá là:

90 x 60 x 42 = 226 800 (cm³)

Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể là:

226 800 : 324 000 = 70%

Lượng nước trong bể chiếm 70% so với lượng nước khi đầy bể.

Bài 3

Giải Bài 3 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống

Cùng xuất phát ở bến A đi đến khu du lịch B, Việt đi xe buýt thì đến nơi lúc 8 giờ 15 phút, Mai đi xe taxi đến nơi lúc 7 giờ 30 phút. Rô-bốt cho biết cùng trên quãng đường AB, thời gian đi của taxi bằng $\frac{2}{{3}}$ thời gian đi của xe buýt.

a) Tính thời gian của mỗi xe ô tô đi trên quãng đường AB.

b) Tính độ dài quãng đường AB. Biết vận tốc của xe buýt là 40 km/h.

Phương pháp giải:

1. Vẽ sơ đồ: coi thời gian đi của taxi (đóng vai trò số bé) gồm 2 phần bằng nhau thì thời gian của xe buýt (đóng vai trò số lớn) gồm 3 phần bằng nhau như thế.

2. Tìm hiệu số phần bằng nhau.

3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

4. Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn).

Quãng đường = Vận tốc x Thời gian.

Lời giải chi tiết:

Bài giải

Đổi 8 giờ 15 phút = 8,25 giờ

9 giờ 30 phút = 9,5 giờ

Thời gian đi của xe buýt dài hơn thời gian đi của taxi là:

9,5 – 8,25 = 1,25 (giờ)

Ta có sơ đồ:

Hiệu số phần bằng nhau là:

3 – 2 = 1 (phần)

Thời gian đi xe taxi là:

1,25 x 2 = 2,5 (giờ)

Thời gian đi xe buýt là:

1,25 x 3 = 3,75 (giờ)

Độ dài quãng đường AB là:

40 x 3,75 = 150 (km)

Đáp số: a) 2,5 giờ; 3,75 giờ

b) 150 km.

Bài 4

Giải Bài 4 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống

Viết số thích hợp vào chỗ chấm.

Một tỉnh miền núi có diện tích khoảng 10 000 km². Hiện tại, mật độ dân số ở tỉnh đó khoảng 80 người/km² (nghĩa là cứ mỗi ki-lô-mét vuông có trung bình 80 người).

Nếu muốn tăng mật độ dân số của tỉnh đó lên 92 người/km²thì:

a) Số dân của tỉnh phải tăng thêm ............... người.

b) Số dân phải tăng thêm bằng ........% số dân hiện tại.

Phương pháp giải:

- Số dân của tỉnh với mật độ 80 người/km² = Diện tích tỉnh x Mật độ dân số.

- Số dân của tỉnh với mật độ 92 người/km² = Diện tích tỉnh x Mật độ dân số.

- Số dân của tỉnh phải tăng lên để mật độ dân số là 92 người/km² = Số dân của tỉnh với mật độ 92 người/km² - Số dân của tỉnh với mật độ 80 người/km².

b) Phần trăm số dân tăng thêm so với số dân hiện tại = Số dân tăng thêm : Số dân hiện tại x 100%.

Lời giải chi tiết:

Bài giải

Số dân của tỉnh với mật độ 80 người/km² là:

10 000 x 80 = 800 000 (người)

Số dân của tỉnh với mật độ 92 người/km² là:

10 000 x 92 = 920 01500 (người)

Muốn tăng mật độ dân số của tỉnh đó là 92 người/km² thì số dân của tỉnh phải tăng thêm số người là:

920 000 – 800 000 = 120 000 (người)

Số dân của tỉnh phải tăng thêm 120 000 người.

Số dân tăng thêm chiếm số phần trăm là:

120 000 : 800 000 x 100% = 15%