-
GIẢI SGK TOÁN 11 KẾT NỐI TRI THỨC VỚI CUỘC SỐNG - MỚI NHẤT
-
Toán 10 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 10 tập 2 - Kết nối tri thức với cuộc sống
Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
Bài 10. Vectơ trong mặt phẳng tọa độ Toán 10 Kết nối tr..
Lý thuyết Vecto trong mặt phẳng tọa độ - SGK Toán 10 Kết nối tri thức
1. TỌA ĐỘ CỦA MỘT VECTO 2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
1. TỌA ĐỘ CỦA MỘT VECTO
+) Trên mặt phẳng, hệ trục gồm hai trục Ox, Oy vuông góc với nhau tại O được gọi là hệ trục tọa độ.
Mặt phẳng chứa hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy hay mặt phẳng Oxy.
+) Vecto đơn vị là vecto hướng là chiều dương, có độ dài bằng 1.
Quy ước: vecto đơn vị của trục Ox là \(\overrightarrow i \), vecto đơn vị của trục Oy là \(\overrightarrow j \).
Điểm O gọi là gốc tọa độ, trục Ox gọi là trục hoành, trục Oy gọi là trục tung.
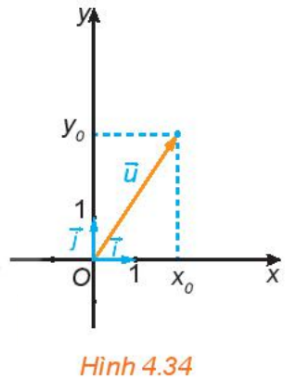
+) Với mỗi vecto \(\overrightarrow u \) trên mặt phẳng Oxy, có duy nhất cặp số \(({x_0};{y_0})\) sao cho \(\overrightarrow u = {x_0}.\overrightarrow i + {y_0}.\overrightarrow j \)
Ta nói vecto \(\overrightarrow u \) có tọa độ \(({x_0};{y_0})\) và viết \(\overrightarrow u = ({x_0};{y_0})\) hoặc \(\overrightarrow u ({x_0};{y_0})\).
Các số \({x_0},{y_0}\) tương ứng được gọi là hoành độ, tung độ của \(\overrightarrow u \).
+) Hai vecto bằng nhau khi và chỉ khi chúng có cùng tọa độ
\(\overrightarrow u (x;y) = \overrightarrow v (x';y') \Leftrightarrow \left\{ \begin{array}{l}x = x'\\y = y'\end{array} \right.\)
2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
+) Cho hai vecto \(\overrightarrow u = (x;y)\) và \(\overrightarrow v = (x';y')\). Khi đó:
\(\begin{array}{l}\overrightarrow u + \overrightarrow v = (x + x';y + y')\\\overrightarrow u - \overrightarrow v = (x - x';y - y')\\k\overrightarrow u = (kx;ky)\quad (k \in \mathbb{R})\end{array}\)
+) Vecto \(\overrightarrow v \;(x';y')\) cùng phương với vecto \(\overrightarrow u \;(x;y) \ne \overrightarrow 0 \)
\( \Leftrightarrow \exists \;k \in \mathbb{R}:x' = kx,\;y' = ky\) hay \(\frac{{x'}}{x} = \frac{{y'}}{y}\) nếu \(xy \ne 0.\)
+) Điểm M có tọa độ \((x;y)\) thì vecto \(\overrightarrow {OM} \) có tọa độ \((x;y)\) và độ dài \(\left| {\overrightarrow {OM} } \right| = \sqrt {{x^2} + {y^2}} \)
+) Với hai điểm \(M(x;y)\) và \(N(x';y')\) thì \(\overrightarrow {MN} = (x' - x;y' - y)\)
Khoảng cách giữa hai điểm M, N là \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{(x' - x)}^2} + {{(y' - y)}^2}} \)
+) Trung điểm M của đoạn thẳng AB có tọa độ là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
+) Trọng tâm G của tam giác ABC có tọa độ là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Bình luận
Chia sẻ
- Giải câu hỏi mở đầu trang 59 SGK Toán 10 tập 1 – Kết nối tri thức
- Giải mục 1 trang 60, 61 SGK Toán 10 tập 1 - Kết nối tri thức
- Giải mục 2 trang 61, 62, 63, 64 SGK Toán 10 tập 1 - Kết nối tri thức
- Giải bài 4.16 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
- Giải bài 4.17 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
