 Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
 Bài 10. Vectơ trong mặt phẳng tọa độ Toán 10 Kết nối tr..
Bài 10. Vectơ trong mặt phẳng tọa độ Toán 10 Kết nối tr..
Giải mục 2 trang 61, 62, 63, 64 SGK Toán 10 tập 1 - Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho u = (2; - 3), v = (4;1), a = (8; - 12 Trong mặt phẳng tọa độ Oxy, cho điểm M(x0, y0). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35) Trong mặt phẳng tọa độ Oxy, cho các điểm M(x;y) và N(x’; y’) Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3). Từ thông tin dự báo được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 61 SGK Toán 10 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = (2; - 3),\overrightarrow v = (4;1),\overrightarrow a = (8; - 12)\).
a) Hãy biểu thị mỗi vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow a \) theo các vectơ \(\overrightarrow i ,\overrightarrow j \).
b) Tìm tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v ,4.\overrightarrow u \).
c) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow u ,\overrightarrow a \).
Phương pháp giải:
a) Vectơ \(\overrightarrow a \) có tọa độ (x;y) thì \(\overrightarrow a = x.\overrightarrow i + y.\overrightarrow j \).
b)
Bước 1: Tính \(\overrightarrow u + \overrightarrow v ,4.\overrightarrow u \) theo các vectơ \(\overrightarrow i ,\overrightarrow j \).
Bước 2: Suy ra tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v ,4.\overrightarrow u \).
c)
Quan sát biểu thị theo các vectơ \(\overrightarrow i ,\overrightarrow j \) của các vectơ \(\overrightarrow u ,\overrightarrow a \) để suy ra mối liên hệ.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow u = (2; - 3)\).
\( \Rightarrow \overrightarrow u = 2.\overrightarrow i + \left( { - 3} \right).\overrightarrow j \).
Tương tự ta có: \(\overrightarrow v = (4;1),\overrightarrow a = (8; - 12)\).
\( \Rightarrow \overrightarrow v = 4.\overrightarrow i + 1.\overrightarrow j ;\overrightarrow a = 8.\overrightarrow i + \left( { - 12} \right).\overrightarrow j \).
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\overrightarrow i + \left( { - 3} \right).\overrightarrow j \\\overrightarrow v = 4.\overrightarrow i + 1.\overrightarrow j \end{array} \right.\) (theo câu a).
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \overrightarrow v = \left( {2.\overrightarrow i + \left( { - 3} \right).\overrightarrow j } \right) + \left( {4.\overrightarrow i + 1.\overrightarrow j } \right)\\4.\overrightarrow u = 4\left( {2.\overrightarrow i + \left( { - 3} \right).\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \overrightarrow v = \left( {2.\overrightarrow i + 4.\overrightarrow i } \right) + \left( {\left( { - 3} \right).\overrightarrow j + 1.\overrightarrow j } \right)\\4.\overrightarrow u = 4.2.\overrightarrow i + 4.\left( { - 3} \right).\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \overrightarrow v = 6.\overrightarrow i + \left( { - 2} \right).\overrightarrow j \\4.\overrightarrow u = 8.\overrightarrow i + \left( { - 12} \right).\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\overrightarrow u = 8.\overrightarrow i + \left( { - 12} \right).\overrightarrow j \\\overrightarrow a = 8.\overrightarrow i + \left( { - 12} \right).\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\overrightarrow u = \overrightarrow a \).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 62 SGK Toán 10 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho điểm \(M({x_o};{y_o})\). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).
a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị \(\overrightarrow {OP} \) theo \(\overrightarrow i \) và tính độ dài của \(\overrightarrow {OP} \) theo \({x_o}\).
b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị \(\overrightarrow {OQ} \) theo \(\overrightarrow j \) và tính độ dài của \(\overrightarrow {OQ} \) theo \({y_o}\).
c) Dựa vào hình chữ nhật OPMQ, tính độ dài của \(\overrightarrow {OM} \) theo \({x_o},{y_o}.\)
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
Phương pháp giải:
a) P biểu diễn hoành độ của điểm M.
b) Q biểu diễn tung độ của điểm M.
c) Tính độ dài của \(\overrightarrow {OM} \) theo các cạnh của hình chữ nhật dựa vào định lí Pytago.
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow {OP} \), \(\overrightarrow {OQ} \) (quy tắc hình bình hành).
Lời giải chi tiết:
a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\).
Ta có: Vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\).
\( \Rightarrow \overrightarrow {OP} = {x_o}.\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\).
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\).
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\).
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \).
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \).
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\overrightarrow j \).
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 6 SGK Toán 10 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho các điểm M(x;y) và N(x’; y’).
a) Tìm tọa độ của các vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \).
b) Biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) và tọa độ của \(\overrightarrow {MN} \).
c) Tìm độ dài của vectơ \(\overrightarrow {MN} \).
Phương pháp giải:
a) Tọa độ của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) chính là tọa độ của M, N.
b) Biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) bằng quy tắc hiệu.
Tìm tọa độ của \(\overrightarrow {MN} \) dựa vào biểu thị theo hiệu ở trên và tọa độ của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) đã biết.
c) Độ dài của vectơ \(\overrightarrow {MN} (a;b)\) là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
a) Vì điểm M có tọa độ (x; y) nên vectơ \(\overrightarrow {OM} \) có tọa độ (x; y).
Và điểm N có tọa độ (x’; y’) nên vectơ \(\overrightarrow {ON} \) có tọa độ (x’; y’).
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \) (quy tắc hiệu).
Mà \(\overrightarrow {OM} \) có tọa độ (x; y); \(\overrightarrow {ON} \) có tọa độ (x’; y’).
\( \Rightarrow \overrightarrow {MN} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\).
c) Vì \(\overrightarrow {MN} \) có tọa độ \(\left( {x' - x;y' - y} \right)\) nên \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {x' - x} \right)}^2} + {{\left( {y' - y} \right)}^2}} \).
LT2
Trả lời câu hỏi Luyện tập 2 trang 6 SGK Toán 10 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x; y) để OABM là một hình hành.
Phương pháp giải:
a) Các điểm O, A, B thẳng hàng khi và chỉ khi hai vectơ \(\overrightarrow {OA} ,\;\overrightarrow {OB} \) cùng phương.
b) OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
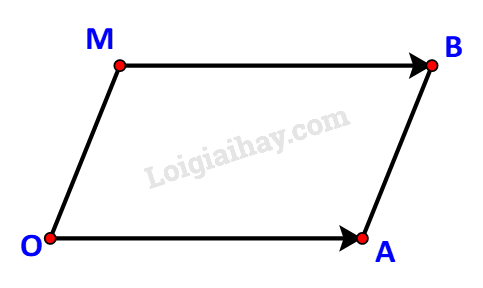
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).
VD
Trả lời câu hỏi Vận dụng trang 64 SGK Toán 10 Kết nối tri thức
Từ thông tin dự báo được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.

Lời giải chi tiết:
Gọi tọa độ điểm M là (x; y).
Theo dự báo, tại thời điểm 9 giờ, tâm bão đã đi được \(\frac{9}{{12}} = \frac{3}{4}\) khoảng cách từ A tới B.
Hay \(AM = \frac{3}{4}.AB \Rightarrow \overrightarrow {AM} = \frac{3}{4}.\overrightarrow {AB} \) (*)
Mà \(\overrightarrow {AM} = \left( {x - 13,8;y - 108,3} \right)\), \(\overrightarrow {AB} = \left( {14,1 - 13,8;106,3 - 108,3} \right) = \left( {0,3; - 2} \right)\).
Do đó \((*) \Leftrightarrow \left\{ \begin{array}{l}x - 13,8 = \frac{3}{4}.0,3\\y - 108,3 = \frac{3}{4}.\left( { - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 14,025\\y = 106,8\end{array} \right.\)
Vậy tọa độ điểm M là (14,025; 106,8).
- Giải bài 4.16 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
- Giải bài 4.17 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
- Giải bài 4.18 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
- Giải bài 4.19 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
- Giải bài 4.20 trang 65 SGK Toán 10 tập 1 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức












Danh sách bình luận