Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam..

Giải Bài 9.1 trang 48 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60

Toán - Văn - Anh - Khoa học tự nhiên...

Đề bài

Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60⁰.

Phương pháp giải - Xem chi tiết

Áp dụng mối liên hệ giữa cạn và góc trong tam giác: Góc đối diện với cạnh lớn hơn là góc lớn hơn.

Lời giải chi tiết

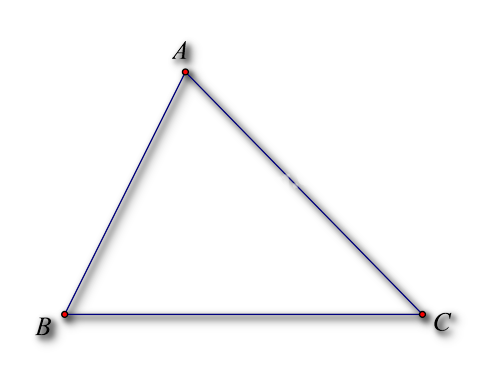
Do cạnh BC dài nhất nên góc A lớn nhất (mối liên hệ giữa cạnh và góc trong tam giác)

\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat A \ge \widehat B\\\widehat A \ge \widehat C\end{array} \right.\)

Nếu \(\widehat A < {60^0} \Rightarrow \widehat B < {60^0};\widehat C < {60^0}\)

\( \Rightarrow \widehat A + \widehat B + \widehat C < {60^0} + {60^0} + {60^0} = {180^0}\) (Vô lí)

Vậy \(\widehat A \ge {60^0}\)

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 14 phiếu

Giải Bài 9.2 trang 48 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABC cân tại A, hai điểm D, E nằm trên đường thẳng BC, D nằm giữa B và C, C nằm giữa D và E. Hãy chứng minh AD < AC < AE.
Giải Bài 9.3 trang 48 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Hãy giải thích tại sao trong tam giác vuông, cạnh huyền dài nhất và trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất
Giải Bài 9.4 trang 48 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC. a)Hãy so sánh hai góc MAB và MAC. b)Tia phân giác của góc BAC cắt BC tại D. Hỏi D thuộc đoạn thẳng MB hay đoạn thẳng MC? Vì sao?

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục