Giải bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức

Từ mẫu số liệu về thuế thuốc lá của 11 thành phố tại một quốc gia, người ta tính được: Giá trị nhỏ nhất bằng 2,5; Q1=36, Q2= 60,Q3} = 100; giá trị lớn nhất bằng 205. a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu? b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này. c) Tìm khoảng tứ phân vị của mẫu số liệu.

Đề bài

Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được:

Giá trị nhỏ nhất bằng 2,5;\({Q_1} = 36\), \({Q_2} = 60\),\({Q_3} = 100\); giá trị lớn nhất bằng 205.

a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?

b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này.

c) Tìm khoảng tứ phân vị của mẫu số liệu.

Phương pháp giải - Xem chi tiết

a) Các điểm \({Q_1},{Q_2},{Q_3}\) chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành 4 phần, mỗi phần chứa 25%.

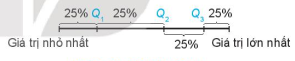
b) Lấy các giá trị sao cho tổng các khoảng là 50%

c) Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\)

Lời giải chi tiết

a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là tỉ lệ thành phố có thuế thuốc lá lớn hơn \({Q_1}\)

=> Có 75%

b) Ta thấy từ giá trị nhỏ nhất đến \({Q_2}\) có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này

=> Ta chọn giá trị thứ nhất là 2,5 và 36.

c) Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 100 - 36 = 64\)

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 13 phiếu

Bài tiếp theo

Giải bài 5.15 trang 88 SGK Toán 10 – Kết nối tri thức
Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg): 2,977 3,155 3,920 3,412 4,236 2,593 3,270 3,813 4,042 3,387 Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.
Giải bài 5.16 trang 88 SGK Toán 10 – Kết nối tri thức
Tỉ lệ thất nghiệp ở một số quốc gia vào năm 2007 (đơn vị %) được cho như sau: 7,8 3,2 7,7 8,7 8,6 8,4 7,2 3,6 5,0 4,4 6,7 7,0 4,5 6,0 5,4 Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.
Giải bài 5.13 trang 88 SGK Toán 10 – Kết nối tri thức
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu: a) Nhân mỗi giá trị của mẫu số liệu với 2. b) Cộng mỗi giá trị của mẫu số liệu với 2.
Giải bài 5.12 trang 88 SGK Toán 10 – Kết nối tri thức
Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau: Không tính toán, hãy cho biết: a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không? b) Mẫu số liệu nào có phương sai lớn hơn?
Giải bài 5.11 trang 88 SGK Toán 10 – Kết nối tri thức
Mỗi khẳng định sau đúng hay sai? (1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn. (2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại. (3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất. (4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp. (5) Các số đo độ phân tán đều không âm.
Giải mục 3 trang 87 SGK Toán 10 tập 1 - Kết nối tri thức
Một mẫu số liệu có tử phân vị thứ nhất là 56 và tứ phân vị thứ ba là 84. Hãy kiểm tra xem trong hai giá trị 10 và 100 giá trị nào được xem là giá trị bất thường.
Giải mục 2 trang 86, 87 SGK Toán 10 tập 1 - Kết nối tri thức
Dùng đồng hồ đo thời gian có độ chia nhỏ nhất đến 0,001 giây để đo 7 lần thời gian rơi tự do của một vật bắt đầu từ điểm A vA=0 đến điểm B. Kết quả đo như sau:
Giải mục 1 trang 84, 85, 86 SGK Toán 10 tập 1 - Kết nối tri thức
Một cổ động viên của câu lạc bộ Everton, Anh đã thống kê điểm số mà hai câu lạc bộ Leicester City và Everton đạt được trong năm mùa giải Ngoại hạng Anh gần đây, từ mùa giải 2014 – 2015 đến mùa giải 2018 - 2019 như sau: Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ: Trong một tuần, nhiệt độ cao nhất trong ngày (đơn vị C) tại hai thành phố Hà Nội và Điện Biên được cho như sau: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của An:
Giải câu hỏi mở đầu trang 84 SGK Toán 10 tập 1 – Kết nối tri thức
Điểm trung bình môn học kì của An và Bình đều là 8,0 nhưng rõ ràng Bình “học đều” hơn An. Có thể dùng những số đặc trưng nào để đo mức độ “học đều”?
Lý thuyết Các số đặc trưng đo độ phân tán
1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ 2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN 3. PHÁT HIỆN SỐ LIỆU BẤT THƯỜNG HOẶC KHÔNG CHÍNH XÁC BẰNG BIỂU ĐỒ HỘP