Giải bài 3.3 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức

LG a

a) ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$.

Phương pháp giải:

Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc $\alpha$ bất kì.

Bước 2: Xác định $\sin \alpha ,\;\cos \alpha$( tương ứng với tung độ và hoành độ của điểm M).

Bước 3: Suy ra đẳng thức cần chứng minh.

Lời giải chi tiết:

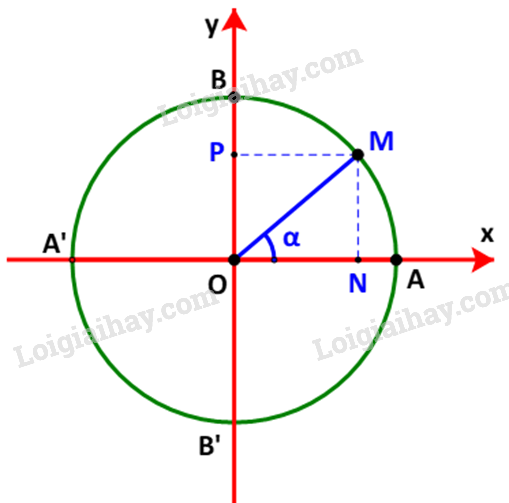
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho $\widehat {xOM} = \alpha$. Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: $\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha  = {x^2}\\{\sin ^2}\alpha  = {y^2}\end{array} \right.$(1)

Mà $\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.$(2)

Từ (1) và (2) suy ra ${\sin ^2}\alpha  + {\cos ^2}\alpha  = O{N^2} + M{N^2} = O{M^2}$ (do $\Delta OMN$ vuông tại N)

$\Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$ (vì OM = 1). (đpcm)

LG b

b) $1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha  \ne {90^o})$

Phương pháp giải:

Bước 1: Viết $\tan \alpha$ dưới dạng $\frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha  \ne {90^o})$, thay vào vế trái.

Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.

Lời giải chi tiết:

Ta có:  $\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha  \ne {90^o})$

$\Rightarrow 1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}$

Mà theo ý a) ta có ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$ với mọi góc $\alpha$

$\Rightarrow 1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}$ (đpcm)

LG c

c) $1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha  < {180^o})$

Phương pháp giải:

Bước 1: Viết $\cot \alpha$ dưới dạng $\frac{{\cos \alpha }}{{\sin \alpha }}\;$, thay vào vế trái.

Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.

Lời giải chi tiết:

Ta có:  $\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha  < {180^o})$

$\Rightarrow 1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}$

Mà theo ý a) ta có ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$ với mọi góc $\alpha$

$\Rightarrow 1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}$ (đpcm)