Bài 4. Bất phương trình bậc hai một ẩn Toán 10 Cánh diều

Giải bài 2 trang 54 SGK Toán 10 tập 1 – Cánh diều

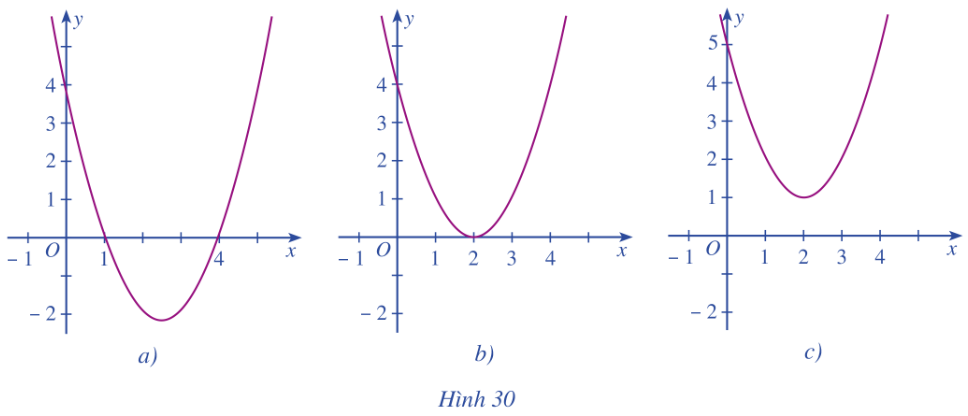
Dựa vào đồ thị hàm số bậc hai f(x) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau:

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;\)\(f\left( x \right) \ge 0;f\left( x \right) \le 0\).

Phương pháp giải - Xem chi tiết

- Quan sát đồ thị.

- Phần phía trên trục hoành biểu diễn tập nghiệm của bất phương trình \(f\left( x \right) > 0\)(không tính giao điểm với đồ thị)

- Phần phía dưới trục hoành biểu diễn tập nghiệm của bất phương trình \(f\left( x \right) < 0\)(không tính giao điểm với đồ thị)

Lời giải chi tiết

Hình 30a:

\(f\left( x \right) > 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\)

\(f\left( x \right) < 0\) có tập nghiệm là \(S = \left( {1;4} \right)\)

\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right] \cup \left[ {4; + \infty } \right)\)

\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left[ {1;4} \right]\)

Hình 30b:

\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\)

\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)

\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)

\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left\{ 2 \right\}\)

Hình 30c:

\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\)

\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)

\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)

\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \emptyset \)

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 13 phiếu

Bài tiếp theo

Giải bài 3 trang 54 SGK Toán 10 tập 1 – Cánh diều
Giải các bất phương trình bậc hai sau:
Giải bài 4 trang 54 SGK Toán 10 tập 1 – Cánh diều
Tìm m để phương trình có nghiệm.
Giải bài 5 trang 54 SGK Toán 10 tập 1 – Cánh diều
Xét hệ toạ độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,2) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.
Giải bài 6 trang 54 SGK Toán 10 tập 1 – Cánh diều
Công ty An Bình thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:
Giải bài 1 trang 54 SGK Toán 10 tập 1 – Cánh diều
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc hai một ẩn? Vì sao?
Giải mục III trang 52, 53 SGK Toán 10 tập 1 - Cánh diều
Tổng chi phí T (đơn vị tính: nghìn đồng) để sản xuất Q sản phẩm được cho bởi biểu thức T=Q^2+30Q + 3300; giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo không bị lỗ (giả thiết các sản phẩm được bán hết)?
Giải mục II trang 50, 51 SGK Toán 10 tập 1 - Cánh diều
a) Lập bảng xét dấu của tam thức bậc hai Giải các bất phương trình bậc hai sau: Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
Giải mục I trang 49 SGK Toán 10 tập 1 - Cánh diều
Quan sát và nêu đặc điểm của biểu thức ở vế trái của bất phương trình 3x^2 - 4x - 8 < 0 a) Cho hai ví dụ về bất phương trình bậc hai một ẩn. b) Cho hai ví dụ về bất phương trình mà không phải là bất phương trình bậc hai một ẩn.
Giải câu hỏi khởi động trang 49 SGK Toán 10 tập 1 - Cánh diều
Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (Hình 25).
Lý thuyết Bất phương trình bậc hai một ẩn - SGK Toán 10 Cánh diều
I. Bất phương trình bậc hai một ẩn II. Giải bất phương trình bậc hai một ẩn